洛谷【P2257】 YY的GCD
出处:http://www.cnblogs.com/peng-ym/p/8652288.html ( 直接去出处那看就好了 )
题目描述
- 神犇YY虐完数论后给傻×kAc出了一题
- 给定N, M,求1<=x<=N, 1<=y<=M且gcd(x, y)为质数的(x, y)有多少对
kAc这种傻×必然不会了,于是向你来请教…… - 多组输入


#include<bits/stdc++.h>
#define LL long long
#define ULL unsigned long long
#define rep(i,j,k) for(int i=j;i<=k;i++)
#define dep(i,j,k) for(int i=k;i>=j;i--)
#define INF 0x3f3f3f3f
#define mem(i,j) memset(i,j,sizeof(i))
#define make(i,j) make_pair(i,j)
#define pb push_back
using namespace std;
const int N=1e7+;
bool vis[N];
int pre[N],sum[N],mu[N],tot;
void init() {
mu[]=;
rep(i,,) {
if(!vis[i]) { pre[++tot]=i; mu[i]=- ; }
rep(j,,tot) {
if(i*pre[j]>N-) break;
vis[i*pre[j]]=;
if(i%pre[j]==) break;
mu[i*pre[j]]=-mu[i];
}
}
rep(j,,tot) {
for(int i=;i*pre[j]<=N-;i++) {
sum[i*pre[j]]+=mu[i];
}
}
rep(i,,N-) sum[i]+=sum[i-];
}
int main() {
init();
int t,n,m;
scanf("%d",&t);
while(t--) {
scanf("%d %d",&n,&m); if(n>m) swap(n,m);
LL ans=;
for(int l=,r;l<=n;l=r+) {
r=min(n/(n/l),m/(m/l));
ans+=1LL*(n/l)*(m/l)*(sum[r]-sum[l-]);
}
printf("%lld\n",ans);
}
return ;
}
洛谷【P2257】 YY的GCD的更多相关文章
- 洛谷 P2257 YY的GCD
洛谷 P2257 YY的GCD \(solution:\) 这道题完全跟[POI2007]ZAP-Queries (莫比乌斯反演+整除分块) 用的一个套路. 我们可以列出答案就是要我们求: \(ans ...
- 洛谷 - P2257 - YY的GCD - 莫比乌斯反演 - 整除分块
https://www.luogu.org/problemnew/show/P2257 求 \(n,m\) 中 \(gcd(i,j)==p\) 的数对的个数 求 $\sum\limits_p \sum ...
- 洛谷 P2257 YY的GCD 题解
原题链接 庆祝: 数论紫题 \(T4\) 达成! 莫比乌斯 \(T1\) 达成! yy 真是个 神犇 前记 之前我觉得: 推式子,直接欧拉筛,筛出个 \(\phi\),然后乱推 \(\gcd\) 就行 ...
- 洛谷 P2257 - YY的GCD(莫比乌斯反演+整除分块)
题面传送门 题意: 求满足 \(1 \leq x \leq n\),\(1 \leq y \leq m\),\(\gcd(x,y)\) 为质数的数对 \((x,y)\) 的个数. \(T\) 组询问. ...
- 洛谷P2257 YY的GCD 莫比乌斯反演
原题链接 差不多算自己推出来的第一道题QwQ 题目大意 \(T\)组询问,每次问你\(1\leqslant x\leqslant N\),\(1\leqslant y\leqslant M\)中有多少 ...
- 洛谷P2257 YY的GCD
今日份是数论 大概是..从小学奥数到渐渐毒瘤 那就简单列一下目录[大雾 同余 质数密度 唯一分解定理 互质 完全剩余系 简化剩余系 欧拉函数 逆元 斐蜀定理 阶(及其性质) 欧拉定理 费马小定理 原根 ...
- 洛谷P2257 YY的GCD(莫比乌斯反演)
传送门 原来……莫比乌斯反演是这么用的啊……(虽然仍然不是很明白) 首先,题目所求如下$$\sum_{i=1}^n\sum_{j=1}^m[gcd(i,j)=prim]$$ 我们设$f(d)$表示$g ...
- 解题:洛谷2257 YY的GCD
题面 初见莫比乌斯反演 有一个套路是关于GCD的反演经常设$f(d)=\sum_{gcd(i,j)==d},g(d)=\sum_{d|gcd(i,j)}$,然后推推推 $\sum\limits_{i= ...
- [洛谷2257]YY的GCD 题解
整理题目转化为数学语言 题目要我们求: \[\sum_{i=1}^n\sum_{i=1}^m[gcd(i,j)=p]\] 其中 \[p\in\text{质数集合}\] 这样表示显然不是很好,所以我们需 ...
- 洛谷 2257 - YY的GCD
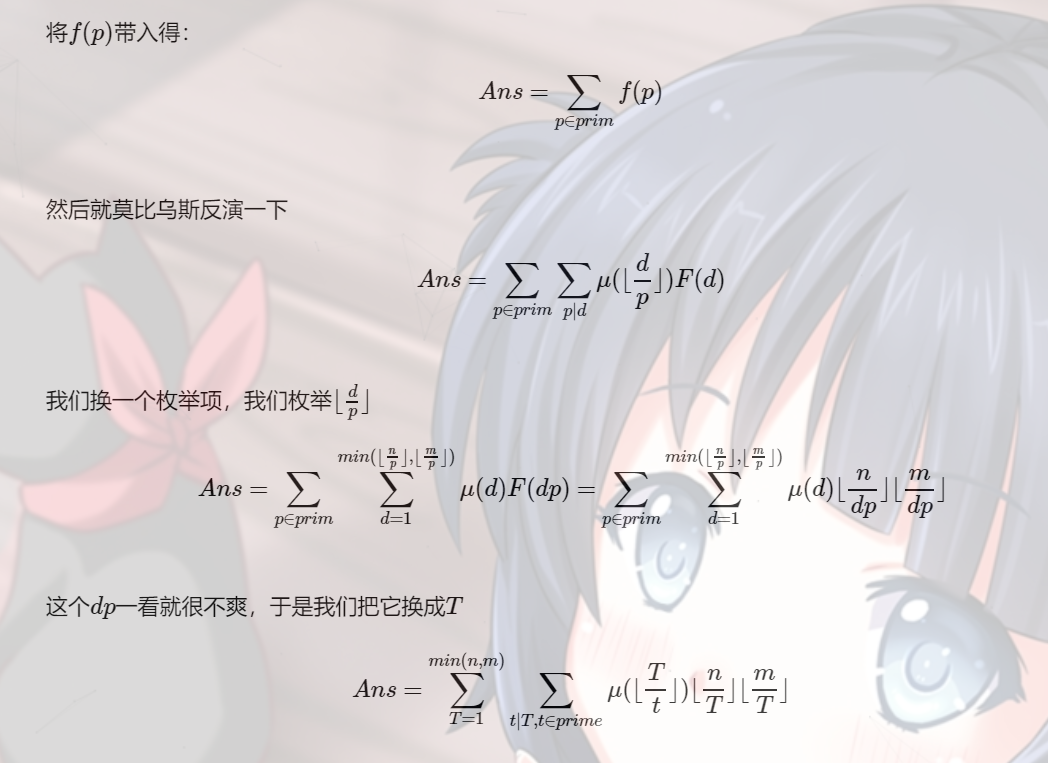
莫比乌斯反演半模板题 很容易可以得到 \[Ans = \sum\limits_{p \in prime} \sum\limits_{d = 1}^{\min (\left\lfloor\frac{a} ...
随机推荐
- 装饰器中functools的用处
定义一个最简单的装饰器 def user_login_data(f): def wrapper(*args, **kwargs): return f(*args, **kwargs) return w ...
- 【GCN】图卷积网络初探——基于图(Graph)的傅里叶变换和卷积
[GCN]图卷积网络初探——基于图(Graph)的傅里叶变换和卷积 2018年11月29日 11:50:38 夏至夏至520 阅读数 5980更多 分类专栏: # MachineLearning ...
- Linux环境下安装Nginx及其使用
https://www.jb51.net/article/136161.htm 一.查看CentOS的版本 ? 1 cat /etc/redhat-release 二.添加资源库 在 CentOS 系 ...
- “最不合格”的SAP应聘者: 从大学生到SAP成都研究院开发工程师
让我们把时光之轮倒拨回2006年,SAP成都研究院刚刚成立的时候,有一位年轻的电子科技大学研究生,网名雷米兰(这名字一看就是AC米兰铁杆粉丝),加入了SAP成都研究院并被派遣到SAP德国总部进行实习. ...
- Spring的启动流程
spring的启动是建筑在servlet容器之上的,所有web工程的初始位置就是web.xml,它配置了servlet的上下文(context)和监听器(Listener),下面就来看看web.xml ...
- SSISDB7:当前正在运行的Package及其Executable
PM问:“Vic,现在ETL Job跑到哪一个Package了,正在执行哪个Task?”,第一次遇到这个问题时,一下就懵逼了,只能硬着头皮说:“我看看”. 在做项目开发时,这个问题很常见,但是,被很多 ...
- Rabbitmq各方法的作用详解
exchange_declare('direct_logs', 'direct', false, false, false);// 这个是申明交换器,如果没有申明就给默认队列的这个交换器,而且发送的类 ...
- idea控制台乱码修改
我的idea当前版本是2019.2.2 试了很多,只有这个有效果 工具类→HELP→Edit Custom VM OPtions中加 -Dfile.encoding=utf-8 然后重启IDEA 这个 ...
- python监控CPU/内存/磁盘,超过指定百分比,发送邮件
#!/usr/bin/python #coding:utf-8 #导入psutil模块 import psutil import yagmail def mail(subject,contents): ...
- Linux内核的目录结构
