洛谷P1886 滑动窗口（POJ.2823 Sliding Window）（区间最值）

To 洛谷.1886 滑动窗口 To POJ.2823 Sliding Window

题目描述

现在有一堆数字共N个数字（N<=10^6），以及一个大小为k的窗口。现在这个从左边开始向右滑动，每次滑动一个单位，求出每次滑动后窗口中的最大值和最小值。

例如：

The array is [1 3 -1 -3 5 3 6 7], and k = 3.

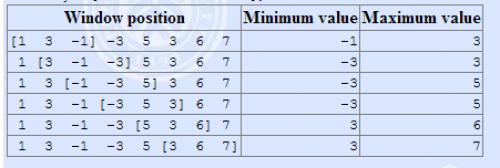
输入输出格式

输入格式：

输入一共有两行，第一行为n,k。

第二行为n个数(<INT_MAX).

输出格式：

输出共两行，第一行为每次窗口滑动的最小值

第二行为每次窗口滑动的最大值

输入输出样例

输入样例#1：

8 3
1 3 -1 -3 5 3 6 7

输出样例#1：

-1 -3 -3 -3 3 3
3 3 5 5 6 7

说明

50%的数据，n<=10^5

100%的数据，n<=10^6

代码：

洛谷70分TLE的线段树

 #include<cstdio>
 #include<algorithm>
 using namespace std;
 const int N=;

 int n,k,From,To,Min[N<<],Max[N<<];

 void read(int &now)
 {
     now=;int f=;char c=getchar();
     while(c<''||c>'')
     {
         if(c=='-')f=-;
         c=getchar();
     }
     while(c>=''&&c<='')now=now*+c-'',c=getchar();
     now*=f;
 }

 inline void PushUp(int rt)
 {
     Min[rt]=min(Min[rt<<],Min[rt<<|]);
     Max[rt]=max(Max[rt<<],Max[rt<<|]);
 }

 void Build(int l,int r,int rt)
 {
     if(l==r)
     {
         int t;
         read(t);
         Min[rt]=Max[rt]=t;
         return;
     }
     int m=(l+r)>>;
     Build(l,m,rt<<);
     Build(m+,r,rt<<|);
     PushUp(rt);
 }

 int QueryMax(int l,int r,int rt,int L,int R)
 {
     if(L<=l && r<=R) return Max[rt];
     int m=(l+r)>>,res=(<<);
     if(L<=m) res=max(res,QueryMax(l,m,rt<<,L,R));
     if(m<R) res=max(res,QueryMax(m+,r,rt<<|,L,R));
     return res;
 }

 int QueryMin(int l,int r,int rt,int L,int R)
 {
     if(L<=l && r<=R) return Min[rt];
     int m=(l+r)>>,res=(<<);
     if(L<=m) res=min(res,QueryMin(l,m,rt<<,L,R));
     if(m<R) res=min(res,QueryMin(m+,r,rt<<|,L,R));
     return res;
 }

 int main()
 {
     read(n);read(k);
     Build(,n,);
     //From=1;To=k;
     for(register int i=;i<=n-k+;i++)//,From++,To++
       printf("%d ",QueryMin(,n,,i,i+k-));
     printf("\n");
     //From=1;To=k;
     for(register int i=;i<=n-k+;i++)//,From++,To++
       printf("%d ",QueryMax(,n,,i,i+k-));
     return ;
 }

TLE

常数优化十分可观的zkw线段树（然而我不会用）

 #include<cstdio>
 #include<algorithm>
 using namespace std;
 const int N=;

 int n,k,M,Tree[N<<];

 void read(int &now)
 {
     now=;int f=;char c=getchar();
     while(c>''||c<'')
     {
         if(c=='-')f=-;
         c=getchar();
     }
     while(c>=''&&c<='')now=(now<<)+(now<<)+c-'',c=getchar();
     now*=f;
 }

 void BuildMin(int n)
 {
     for(int i=M-;i;--i)
       Tree[i]=min(Tree[i<<],Tree[i<<|]);
 }

 void BuildMax(int n)
 {
     for(int i=M-;i;--i)
       Tree[i]=max(Tree[i<<],Tree[i<<|]);
 }

 int QueryMin(int s,int t,int res)
 {
     for(s+=M,t+=M;s^t^;s>>=,t>>=)
     {
         if(~s&) res=min(res,Tree[s^]);
         if(t&) res=min(res,Tree[t^]);
     }
     return res;
 }

 int QueryMax(int s,int t,int res)
 {
     for(s+=M,t+=M;s^t^;s>>=,t>>=)
     {
         if(~s&) res=max(res,Tree[s^]);
         if(t&) res=max(res,Tree[t^]);
     }
     return res;
 }

 int main()
 {
     read(n);read(k);
     for(M=;M<=n+;M<<=);
     for(int i=M+;i<=M+n;i++)
       read(Tree[i]);
     BuildMin(n);
     for(int i=;i<=n-k;++i)
       printf("%d ",QueryMin(i,i+k+,1e9));
     printf("\n");
     BuildMax(n);
     for(int i=;i<=n-k;++i)
       printf("%d ",QueryMax(i,i+k+,-1e9));
     return ;
 }

AC