Gym 102091A： Flying Squirrel（RMQ）

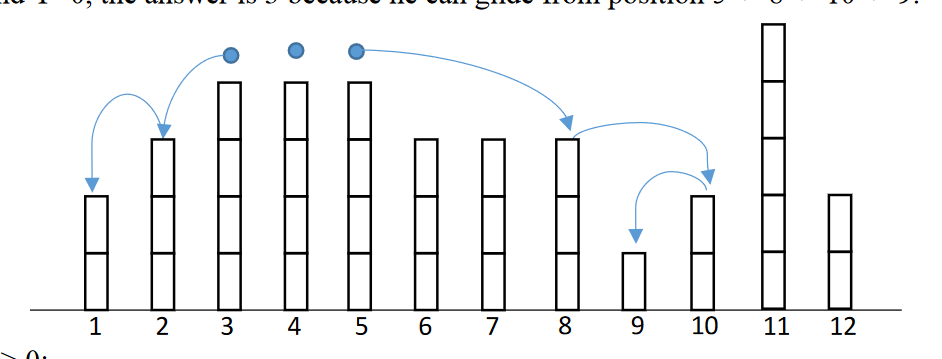
题意：如图，有N个柱子，每次我可以从高柱子X到低柱子Y，而且需要满足中间的柱子都小于X的高度。

思路：现在有Q次询问，每次给定（X，Y），(如果ht[X]<ht[Y]，则交换XY)，问X为起点，Y为终点的最长路径。 如果Y为0，你可以选择任一点为终点。

每次我们把当前dfs的区间最高的几个柱子（假设高度为H）抽出来，它们把当前区间划分为了几个小区间，可以把这些高的柱子看成根，那么被夹在中间的区间就是子树，再去dfs深入中间的区间即可。   最后假如要从X到Y，如果它们之间没有更高的，答案就是深度差。

由于每个柱子只被当成一次根，所的复杂度是O(N)的，加上RMQ找区间最大值，总的时间是O(NlogN)的。

#include<bits/stdc++.h>
#define rep(i,a,b) for(int i=a;i<=b;i++)
using namespace std;
const int maxn=;
int h[maxn],dep[maxn],ans[maxn];
int mx[][maxn],Log[maxn];
int Max(int a,int b){ return h[a]>=h[b]?a:b;}
int find(int L,int R)
{
    int k=Log[R-L+];
    return Max(mx[k][L],mx[k][R-(<<k)+]);
}
int solve(int L,int R,int d)
{
    if(L>R) return -;
    int p=find(L,R); dep[p]=d;
    ans[p]=solve(L,p-,d+)+;
    int res=ans[p];
    while(p<R){
        int q=find(p+,R);
        if(h[q]!=h[p]) break;
        dep[q]=d;
        int t=solve(p+,q-,d+)+;
        res=max(res,t);
        ans[p]=max(ans[p],t);
        ans[q]=t;
        p=q;
    }
    ans[p]=max(ans[p],solve(p+,R,d+)+);
    res=max(res,ans[p]);
    return res;
}
int main()
{
    int N,M,L,R;
    scanf("%d%d",&N,&M);
    rep(i,,N) scanf("%d",&h[i]);
    Log[]=-;
    rep(i,,N) Log[i]=Log[i>>]+;
    rep(i,,N) mx[][i]=i;
    for(int i=;(<<i)<=N;i++)
     for(int j=;j+(<<i)-<=N;j++)
      mx[i][j]=Max(mx[i-][j],mx[i-][j+(<<(i-))]);
    solve(,N,);
    rep(i,,M){
        scanf("%d%d",&L,&R);
        if(h[L]<h[R]) swap(L,R);
        if(!R) printf("%d\n",ans[L]);
        else {
           if(L==R) puts("");
           else {
              int p;
              if(L<R) p=find(L+,R);
              else p=find(R,L-);
              if(h[p]>=h[L]) puts("");
              else printf("%d\n",dep[R]-dep[L]);
           }
        }
    }
    return ;
}