牛客多校第十场-D- Rikka with Prefix Sum

链接：https://www.nowcoder.com/acm/contest/148/D
来源：牛客网

Prefix Sum is a useful trick in data structure problems.
For example, given an array A of length n and m queries. Each query gives an interval [l,r] and you need to calculate . How to solve this problem in O(n+m)? We can calculate the prefix sum array B in which B_i is equal to . And for each query, the answer is B_r-B_l-1.

Since Rikka is interested in this powerful trick, she sets a simple task about Prefix Sum for you:

Given two integers n,m, Rikka constructs an array A of length n which is initialized by A_i = 0. And then she makes m operations on it.

There are three types of operations:
1. 1 L R w, for each index i ∈ [L,R], change A_i to A_i + w.
2. 2, change A to its prefix sum array. i.e., let A' be a back-up of A, for each i ∈ [1,n], change A_i to .
3. 3 L R, query for the interval sum .

输入描述:

The first line contains a single number t(1≤ t ≤ 3), the number of the testcases.

For each testcase, the first line contains two integers n,m(1 ≤ n,m ≤ 10

⁵

). 

And then m lines follow, each line describes an operation(1 ≤ L ≤ R≤ n, 0 ≤ w ≤ 10

⁹

). 

The input guarantees that for each testcase, there are at most 500 operations of type 3.

输出描述:

For each query, output a single line with a single integer, the answer modulo 998244353.

输入例子:

1
100000 7
1 1 3 1
2
3 2333 6666
2
3 2333 6666
2
3 2333 6666

输出例子:

13002
58489497
12043005

-->

示例1

输入

1
100000 7
1 1 3 1
2
3 2333 6666
2
3 2333 6666
2
3 2333 6666

输出

13002
58489497
12043005

操作有两种，1操作是给l-r区间内的数都加w，2操作是让这个数列变为它的前缀和序列
我们知道，2操作之后得到的新的序列差分之后就是操作前的序列，所以如果只有2操作的话，就是给你一个差分了很多次之后的序列求原序列
但是它还有1操作，1操作对于差分的级别没有变化，但我们知道在原来的序列的l-r区间+w，其实就是在它的差分序列l处+w，r+1处-w
那么现在的问题就在于在这样的一个差分序列的表格中，如果我们在某个点+w，造成的影响是什么

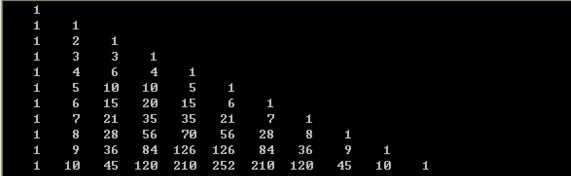
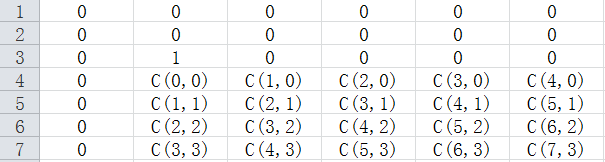
我们发现在一个点+w之后，影响的是它右下角的所有点，每个行的系数是杨辉三角的一列，所以如果在(i,j)点+w，那么(x,y)点的系数为C(x-ai+y-j-,x-i-)

然后3操作不超过500次，所以我们就记录下每次操作，然后对每次询问O(n)计算即可

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int p=;
const int N=2e5+;
int n,m,T,op,l,r,w,cnt;
struct orz{
    int x,pos,w;
}a[N];
ll fac[N],inv[N];
ll poww(ll x,int y)
{
    x%=p;
    ll ret=;
    while (y)
    {
        if (y&) ret=ret*x%p;
        x=x*x%p;
        y>>=;
    }
    return ret;
}
void pre()
{
    fac[]=;
    for (int i=;i<N;i++) fac[i]=fac[i-]*i%p;
    inv[N-]=poww(fac[N-],p-);
    for (int i=N-;i>=;i--) inv[i]=inv[i+]*(i+)%p;
}
ll C(int a,int b)
{
    if (b>a||b<) return ;
    return fac[a]*inv[b]%p*inv[a-b]%p;
}
ll solve(int x,int y)
{
    ll ret=;
    for (int i=;i<=cnt;i++)
    {
        if (a[i].x<=x&&a[i].pos<=y)
            ret=(ret+C(x-a[i].x+y-a[i].pos-,x-a[i].x-)*(ll)a[i].w%p)%p;
    }
    return ret;
}
int main()
{
    scanf("%d",&T);
    pre();
    while (T--)
    {
        scanf("%d%d",&n,&m);
        int now=;
        cnt=;
        while (m--)
        {
            scanf("%d",&op);
            if (op==)
            {
                scanf("%d%d%d",&l,&r,&w);
                cnt++; a[cnt].x=now-; a[cnt].pos=l; a[cnt].w=w%p;
                cnt++; a[cnt].x=now-; a[cnt].pos=r+; a[cnt].w=-w%p;
            }
            else if (op==) now++;
            else
            {
                scanf("%d%d",&l,&r);
                ll ans=((solve(now+,r)-solve(now+,l-))%p+p)%p;
                printf("%lld\n",ans);
            }
        }
    }
    return ;
}