空间谱专题02：波束形成（Beamforming）

作者：桂。

时间：2017-08-22  10:56:45

链接：http://www.cnblogs.com/xingshansi/p/7410846.html

---

前言

本文主要记录常见的波束形成问题，可以说空间谱估计是波束形成基础上发展而来，在系统论述空间谱之前，有必要分析一些Beamforming的基本特性。

一、波束形成模型

以均匀线阵为例：

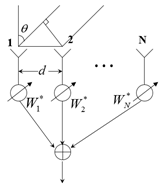
按窄带模型分析：

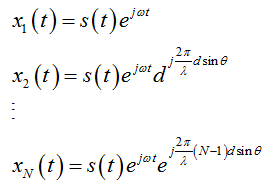
可以写成矩阵形式：

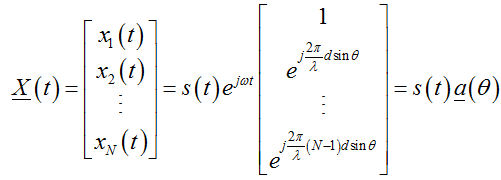
其中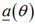为方向矢量或导向矢量（Steering Vector），波束形成主要是针对各个接收信号X进行权重相加。

二、波束形成基本理论

　　A-波束形成

权重相加：

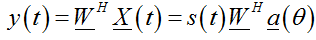
不同的波束形成，就是不同的权重W。

　　B-瑞利限

以均匀直角窗为例：

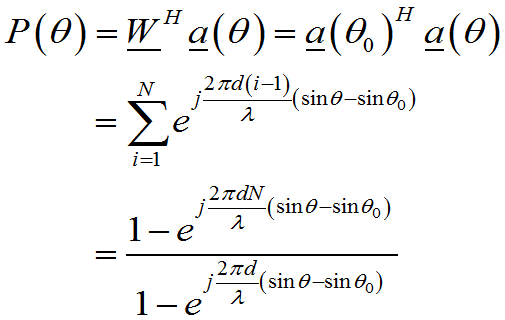
得出方向图：

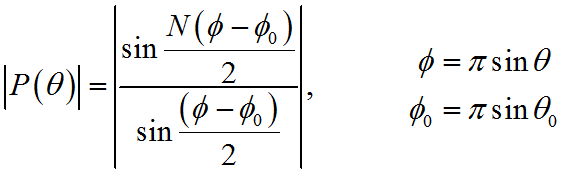
主瓣宽度正比于孔径宽度的倒数：

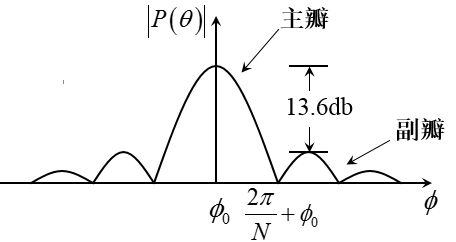
因为孔径的限制，造成波束宽度存在限制（不会无限制小），近而落在主瓣波束内部的两个信号便会混在一起而分不清，这就存在瑞利限的问题。

直角窗主瓣宽度为：

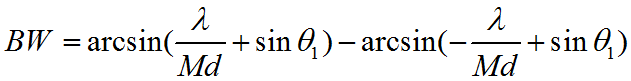
其中λ为入射波长，theta1为入射角，Md为阵列孔径。

　　C-常见窗函数

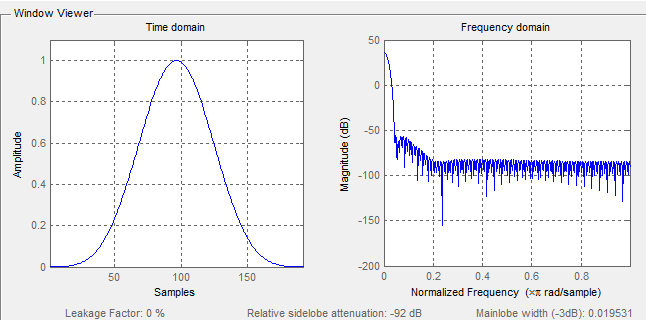
对于空间不同的阵列信号，类似采样分析（空域采样），自然可以加窗进行处理，不加窗可以认为是直角窗，另外也可以选择汉明窗、hanning窗等等。

加窗可以改变波束宽度以及主瓣、副瓣等特性，可以借助MATLAB 的wvtool观察不同窗函数特性。

N = 192;
w = window(@blackmanharris,N);
wvtool(w)

　　D-DFT实现

阵列的采样间隔是相位信息：

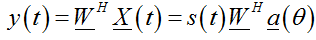
这就类似于频域变换，只不过这里的相位信息：对应的不是频率，而是不同位置，可以看作空域的变换。

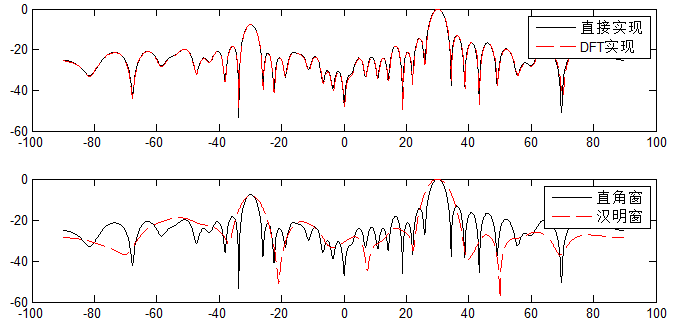
分别对阵列信号进行直接加权、加窗、DFT实现：

function x = StatSigGenerate(M,N,DOA,SNR,SignalMode,lambda,d)

ld = length(DOA);
if strcmp(SignalMode,'Independent')
    st = randn(ld,N)+1j*randn(ld,N);
elseif strcmp(SignalMode,'Coherent')
    st = [];
    st1 = randn(1,N)+1j*randn(1,N);
    for k = 1:ld
        st = [st;st1];
    end
end
st = st/sqrt(trace(st*st'/N)/ld);
nt = randn(M,N)+1j*randn(M,N);
nt = nt/sqrt(trace(nt*nt'/N)/M);

SNR = ones(1,ld)*SNR;
Amp = diag(10.^(SNR/20));
A = exp(1j*2*pi*[0:M-1]'*sind(DOA)*d/lambda);
x = A*Amp*st+nt;
end

　　主程序：

clc;clear all;close all
M = 32;
DOA = [-30 30];
SNR = 10;
theta = -90:.1:90;
len = length(theta);
SignalMode = 'Independent';
fc = 1e9;
c = 3e8;
lambda = c/fc;
d = lambda/2;
N = 100;%snap points
x = StatSigGenerate(M,N,DOA,SNR,SignalMode,lambda,d);
R_hat = 1/N*x*x';
output = zeros(3,len);
for i = 1:len
    a = exp(1j*2*pi*[0:M-1]'*sind(theta(i))*d/lambda);
    W = (inv(R_hat)*a)*(1./(a'*inv(R_hat)*a));
    output(1,i) = mean(abs(W'*x),2);
    output(2,i) = 1./(a'*inv(R_hat)*a);
    output(3,i) = a'*x*ones(N,1);
end
output = abs(output);
output = output - repmat(mean(output.')',1,size(output,2));
output = output./repmat(max(output.')',1,size(output,2));
%plot
plot(theta,output(1,:),'k',theta,output(2,:),'r--',theta,output(3,:),'b');
legend('MVDR 波束','MVDR 谱','固定权重 波束');

　　对应结果图：

　　E-自适应波束形成

直接相加也好、加窗也好，都是固定的权重系数，没有考虑到信号本身的特性，所以如果结合信号本身去考虑就形成了一系列算法：自适应波束形成。

这类步骤通常是：

1）给定准则函数；

2）对准则函数进行求解。

准则常用的有：信噪比（snr）最大准则、均方误差最小准则（MSE）、线性约束最小方差准则（LCMV）、最大似然准则（ML）等等；

求解的思路大体分两类：1）直接求解，例如MVDR中的求解；2）也可以利用梯度下降的思想，如随机梯度下降、批量梯度下降、Newton-raphson等方法，不再详细说明。

以MVDR举例：

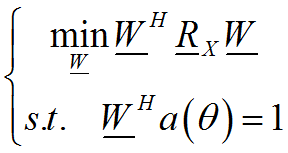
这里采用直接求解的思路：

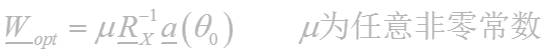
将求解的W带入

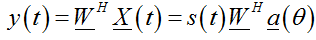
即可得到波束形成。

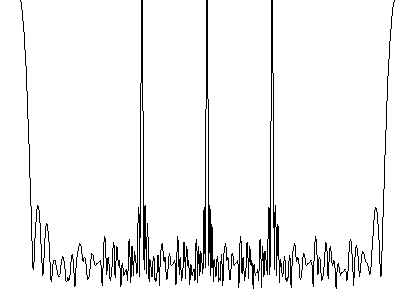
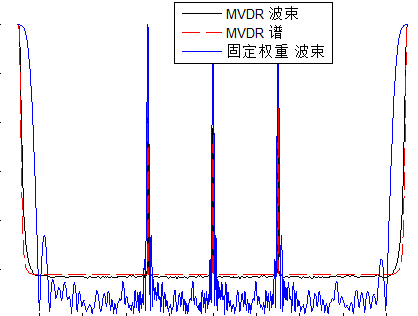
　　F-栅瓣现象

栅瓣是一类现象，对应干涉仪就是相位模糊（相位超过2*pi），对应到Beamforming就是栅瓣问题，具体不再论述，给出现象（同样的波束，在不同的位置分别出现）：

　　G-波束形成与空间谱

之前分析过MVDR的方法，得到的输出（含有约束的最小均方误差准则）为：

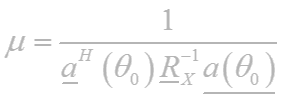
有时候也称这个输出为空间谱，其实就是|y²(t)|，但这个与MUSIC等算法的谱还不是一回事，只是有时候也被称作空间谱，所以这里多啰嗦几句，分析这个说法的来源。

已知N个采样点的信号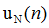，对其进行傅里叶变换：

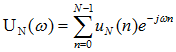
进一步得到功率谱密度：

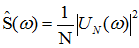
根据上文的分析：y(t)其实对应的就是空域变换（可借助DFT实现），类比于时频处理中的频域变换。而这里又可以看到频域变换的平方/长度，对应就是功率谱，这是频域的分析。

对应到空域，自然就是|y²(t)|/长度，对应空间谱，长度只影响比例关系，所以MVDR的最小方差输出被称作：空间谱也是合适的。

给出一个测试（这里如果），对比MVDR的y(t)、MVDR功率谱以及普通Beamforming的结果：

clc;clear all;close all
M = 32;
DOA = [-30 30];
SNR = 10;
theta = -90:.1:90;
len = length(theta);
SignalMode = 'Independent';
fc = 1e9;
c = 3e8;
lambda = c/fc;
d = lambda/2;
N = 100;%snap points
x = StatSigGenerate(M,N,DOA,SNR,SignalMode,lambda,d);
R_hat = 1/N*x*x';
output = zeros(3,len);
for i = 1:len
    a = exp(1j*2*pi*[0:M-1]'*sind(theta(i))*d/lambda);
    W = (inv(R_hat)*a)*(1./(a'*inv(R_hat)*a));
    output(1,i) = mean(abs(W'*x),2);
    output(2,i) = 1./(a'*inv(R_hat)*a);
    output(3,i) = a'*x*ones(N,1);
end
output = abs(output);
output = output - repmat(mean(output.')',1,size(output,2));
output = output./repmat(max(output.')',1,size(output,2));
%plot
plot(theta,output(1,:),'k',theta,output(2,:),'r--',theta,output(3,:),'b');
legend('MVDR 波束','MVDR 谱','固定权重 波束');

　　对应结果：

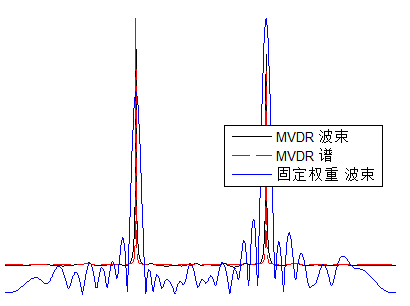
如果将d = lambda/2;改为d = lambda/0.5;，自然就有了栅瓣：