android apk打包编译好的so

加入so到apk有多种方法

1.build.gradle(Module)中android子项中加入以下代码,并将so放到到armeai/armeabi-v7a 子目录下

sourceSets {
    main {
        jniLibs.srcDirs = ['libs/lib']
    }
}

defaultConfig中加入以下

    defaultConfig {

        ndk {
            abiFilters "armeabi"
        }
    }

　　

将so放入libs/armeabi目录

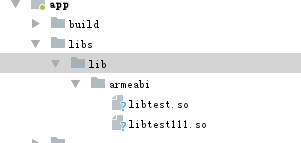
2.直接将so放入到apk中，重新打包签名，但这种方法经常测试情况下很麻烦。