pip install .whl文件时is not a supported wheel on this platform.解决方法

 首先，在python中输入import pip和print(pip.pep425tags.get_supported())，从而获取pip支持的文件名和版本。

somnus@somnus-HP-Pavilion-Notebook:~$ python
Python 2.7.15rc1 (default, Nov 12 2018, 14:31:15)
[GCC 7.3.0] on linux2
Type "help", "copyright", "credits" or "license" for more information.
>>> import pip
>>> print(pip.pep425tags.get_supported())
[('cp27', 'cp27mu', 'manylinux1_x86_64'), ('cp27', 'cp27mu', 'linux_x86_64'), ('cp27', 'none', 'manylinux1_x86_64'), ('cp27', 'none', 'linux_x86_64'), ('py2', 'none', 'manylinux1_x86_64'), ('py2', 'none', 'linux_x86_64'), ('cp27', 'none', 'any'), ('cp2', 'none', 'any'), ('py27', 'none', 'any'), ('py2', 'none', 'any'), ('py26', 'none', 'any'), ('py25', 'none', 'any'), ('py24', 'none', 'any'), ('py23', 'none', 'any'), ('py22', 'none', 'any'), ('py21', 'none', 'any'), ('py20', 'none', 'any')]

 然后，选择支持的.whl文件下载即可，如下图，由于支持('cp27', 'cp27mu', 'manylinux1_x86_64')，所以可下载opencv_python-3.4.3.18-cp27-cp27mu-manylinux1_x86_64.whl。

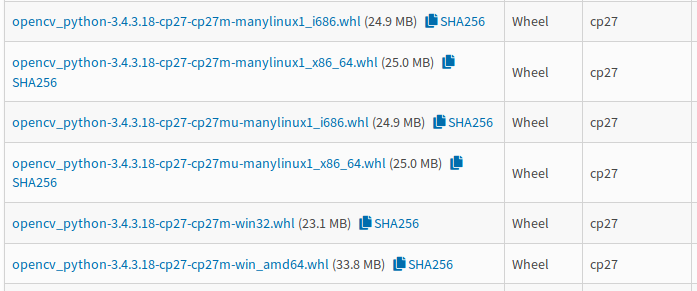
PS：上述方法有时会报错：

>>> import pip
>>> print(pip.pep425tags.get_supported())
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
AttributeError: 'module' object has no attribute 'pep425tags'

此时，对于python2.7，可采用：

>>> import wheel.pep425tags
>>> print(wheel.pep425tags.get_supported())

解决方案参考：https://stackoverflow.com/questions/50248524/module-pip-has-no-attribute-pep425tags