动态规划-区间dp-Palindrome Removal

2019-11-09 10:31:09

问题描述：

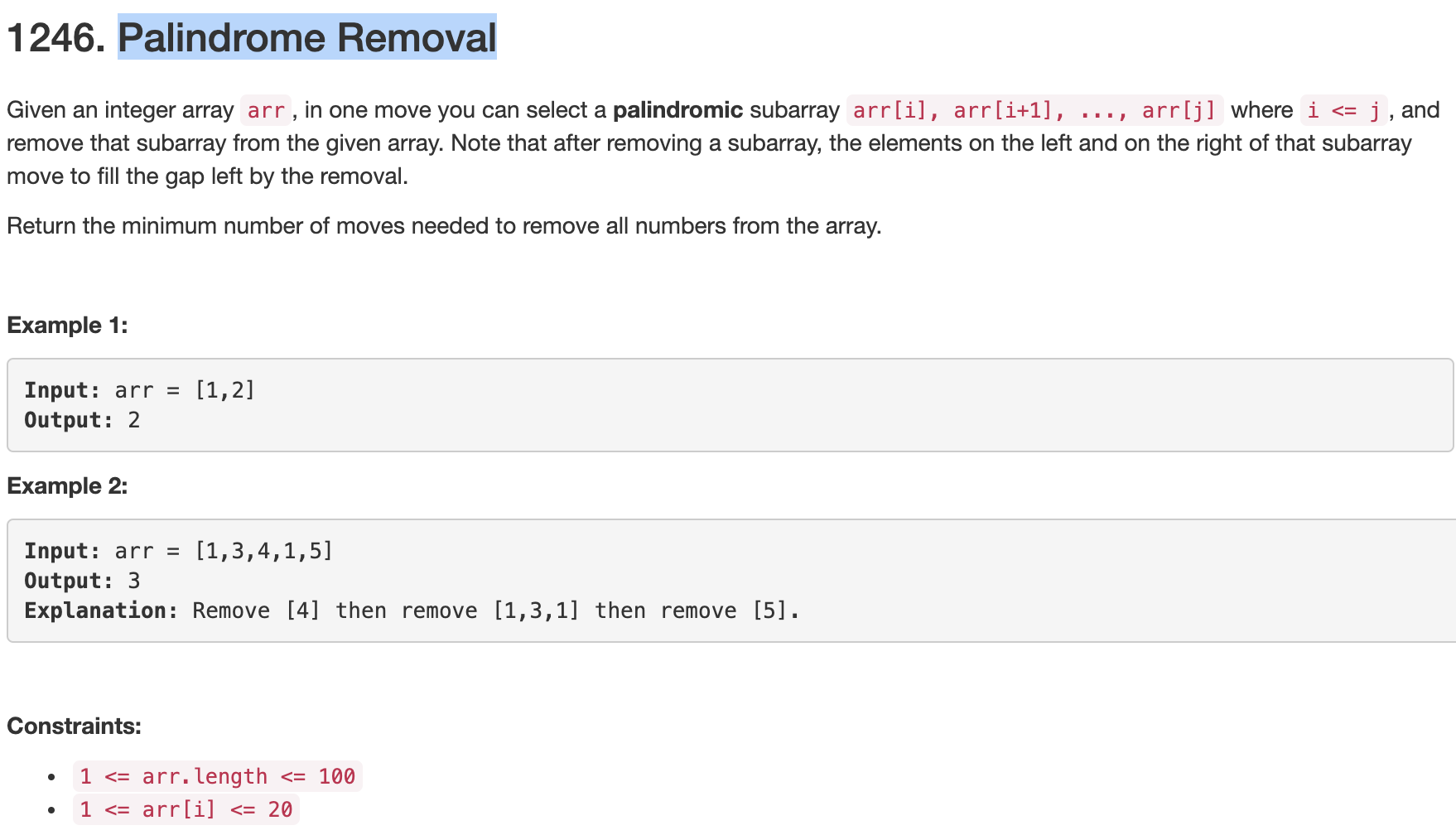
问题求解：

n = 100，典型的O(n ^ 3)的动规问题。一般来说这种O(n ^ 3)的问题可以考虑使用区间dp来解决。

区间dp是典型的三层结构，最外围枚举区间长度，中间层枚举起点，最里层枚举截断点，因此区间dp的时间复杂度往往为O(n ^ 3)。

    public int minimumMoves(int[] arr) {
        int n = arr.length;
        int[][] dp = new int[n + 1][n + 1];
        for (int i = 0; i < n; i++) dp[i][i] = 1;
        for (int len = 2; len <= n; len++) {
            for (int i = 0; i <= n - len; i++) {
                int j = i + len - 1;
                dp[i][j] = 1 + dp[i + 1][j];
                if (arr[i] == arr[i + 1]) dp[i][j] = Math.min(dp[i][j], 1 + dp[i + 2][j]);
                for (int k = i + 2; k <= j; k++) {
                    if (arr[k] == arr[i]) {
                        dp[i][j] = Math.min(dp[i][j], dp[i + 1][k - 1] + dp[k + 1][j]);
                    }
                }
            }
        }
        return dp[0][n - 1];
    }