【图机器学习】cs224w Lecture 16 - 图神经网络的局限性

Capturing Graph Structure
- Graph Isomorphism Network
Vulnerability to Noise

转自本人：https://blog.csdn.net/New2World/article/details/106626551

这一个 Lecture 前还有一个关于 Knowledge Graph 的 slide 我打算跳过，因为 KG 我现在还没有深入研究，可能以后有空会系统地写一个系列，因此现在就不要先入为主了。后面也还有一个 slide 讲 GNN 的应用的，其实就是将前面的内容投入实际场景，没有太多新的 technique，因此也就不整理了。

而这一个 Lecture 我感觉才是比较重要的，它介绍了 GNN 的一些缺陷和限制。

Capturing Graph Structure

GNN 的模式是将一个节点根据它周围的图结构展开成一个计算图，然后做 aggregation。这么看来 GNN 的目的和功能就是抽象图结构，那为什么说这反而是它的 limitation 呢？我们针对现有的 GNN 的模型来逐个分析：

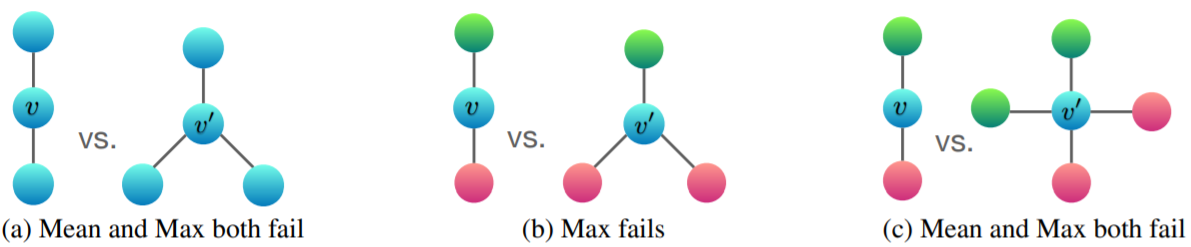
首先是 GCN，它的 aggregation 使用的是 mean pooling。对于上图中情况 (a) 和 (c)，节点 v 和 v' 使用 mean pooling 得到的结果是一样的，然而这两个的结构明显不同。

然后是 GraphSAGE，它的 aggregation 使用的是 max pooling。对于图中情况 (a) 和 (b) 它都不行，因为 (a) 的 max 都是蓝色点，而 (b) 的 max 要么是红色要么是绿色，反正 v 和 v' 得到的结果都一样，因而无法区分这两个不同的图结构。

那么问题到底出现在哪里？很显然是 aggregation 函数。理想情况下，我们希望 aggregation 函数是 injective 的，即内射的。这样就能形成一个一对一的关系，将任何不同的输入映射到不同的输出。max pooling 和 mean pooling 显然不满足这个条件。

这里有个 Theorem，说任何内射的 multi-set 函数都能被表示为 \(\phi(\sum\limits_{x\in S}f(x))\) 其中 \(\phi(\cdot)\) 和 \(f(\cdot)\) 都是非线性函数。但问题是如何定义这两个关键性的函数？这还不简单，MLP 呗。

Graph Isomorphism Network

由此 GIN 诞生了，它的 aggregation 采用 MLP + sum pooling。只要 MLP 设计训练得好，它就是 injective 的。如此一来就能将对图的分辨能力 discriminative power 最大化。那么这个分辨能力到底有多强呢？

回答这个问题，首先需要了解什么事 Weisfeiler-Lehman Graph Isomorphism Test，它是一种能区分现实世界中大部分图结构的方法。形象地理解， WL test 对展开后的各个节点染色，不同的展开结构对应不同颜色，然后通过对比节点颜色和对应数量来判断是否是 isomorhpism。

这和 GIN 在操作上异曲同工，因此理论上来说 WL test 是 GIN 的上界。然而 WL test 也并非打遍天下无敌手，遇到类似下面这种图 WL test 也会犯错，因为每个节点周围的局部展开图都一样。

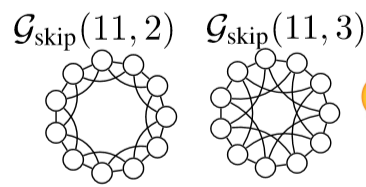
Vulnerability to Noise

其实这个问题可以归结于数据“攻击”，即图像中通过修改部分不易被人眼察觉的像素来达到 adversarial attack 的目的。对于 graph，这种“攻击”是怎么实现的？假设要“攻击”某购物网站，使得它给特定用户瞎推荐东西。分两种情况讨论

能获得这个特定用户的账号，那么事情就简单了。可以通过
- 修改该用户的信息，比如性别、年龄。这会导致系统推荐对应性别和年龄段可能感兴趣的东西；
- 关注收藏一些奇奇怪怪的商品；
- 取消关注一些已关注收藏的商品；
如果无法获得这个特定账号，那我们就“黑掉”几个 Ta 的朋友作为 attacker
- 修改这些 attacker 的用户信息；
- 关注奇怪的东西；
- 取消关注和目标账号的关注相关的东西；

用数学来表示 noise 对 GCN 的影响如下

好，formulation 出来了，解！不好意思，解不了…… 原因有二：其一，图结构上的修改是离散的，不能单纯的用梯度下降来优化；其二，内循环需要重新训练 GCN，太奢侈了。因此需要用 approx. 的方法来近似，比如用贪心算法一步一步的修改图结构。这里没有介绍太多细节，只是提到了 18 年 KDD 的一片文章可以参考。不过由此我们得到的结论是 GNN 对对抗攻击不具有鲁棒性。

至此，cs224w 图机器学习系列更新完毕。之后不定时会整理更新一些之前看过的论文，也会继续新的系列。