• 不是一个机器学习算法
  • 是一种基于搜索的优化方法
  • 作用：最小化一个损失函数
  • 梯度上升法：最大化一个效用函数
import matplotlib.pyplot as plt

import numpy as np

plot_x = np.linspace(-1, 6, 141)

# 损失函数

plot_y = (plot_x - 2.5) ** 2 - 1

plt.plot(plot_x, plot_y)

plt.scatter(plot_x[:70:10], plot_y[: 大专栏  Introduction Of Gradient Descent70:10])

plt.xlabel("param theta")

plt.ylabel("loss func J")

plt.show()

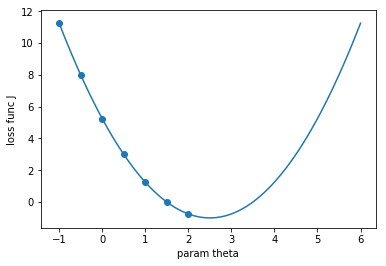
  • 在直线和曲线方程中，导数代表切线的斜率
  • 导数代表theta单位变化时，J相应的变化
  • 导数可以代表方向，对应J增大的方向

我们将θ向导数小的方向移动，来获得极值，如下式

  • η被称为学习率（learning rate）
  • η的取值影响获得最优解的速度
  • η取值不合适，设置得不到最优解
  • η是梯度下降法的一个超参数

η取值影响

  • 过小，收敛速度慢
  • 过大，可能导致不收敛

注意

  • 并不是所有函数都有唯一的极值点（可能会找到局部最优解，并不是全局最优解）
  • 多次运行，随机化初始点
  • 梯度下降法的初始点也是一个超参数

Introduction Of Gradient Descent的更多相关文章

  1. （转）Introduction to Gradient Descent Algorithm (along with variants) in Machine Learning

    Introduction Optimization is always the ultimate goal whether you are dealing with a real life probl ...

  2. (转) An overview of gradient descent optimization algorithms

    An overview of gradient descent optimization algorithms Table of contents: Gradient descent variants ...

  3. 机器学习-随机梯度下降（Stochastic gradient descent）

    sklearn实战-乳腺癌细胞数据挖掘(博主亲自录制视频) https://study.163.com/course/introduction.htm?courseId=1005269003& ...

  4. An overview of gradient descent optimization algorithms

    原文地址:An overview of gradient descent optimization algorithms An overview of gradient descent optimiz ...

  5. 【论文翻译】An overiview of gradient descent optimization algorithms

    这篇论文最早是一篇2016年1月16日发表在Sebastian Ruder的博客.本文主要工作是对这篇论文与李宏毅课程相关的核心部分进行翻译. 论文全文翻译: An overview of gradi ...

  6. 梯度下降（Gradient Descent）小结

    在求解机器学习算法的模型参数,即无约束优化问题时,梯度下降(Gradient Descent)是最常采用的方法之一,另一种常用的方法是最小二乘法.这里就对梯度下降法做一个完整的总结. 1. 梯度 在微 ...

  7. 机器学习基础——梯度下降法（Gradient Descent）

    机器学习基础--梯度下降法(Gradient Descent) 看了coursea的机器学习课,知道了梯度下降法.一开始只是对其做了下简单的了解.随着内容的深入,发现梯度下降法在很多算法中都用的到,除 ...

  8. 线性回归、梯度下降（Linear Regression、Gradient Descent）

    转载请注明出自BYRans博客:http://www.cnblogs.com/BYRans/ 实例 首先举个例子,假设我们有一个二手房交易记录的数据集,已知房屋面积.卧室数量和房屋的交易价格,如下表: ...

  9. Proximal Gradient Descent for L1 Regularization

    [本文链接:http://www.cnblogs.com/breezedeus/p/3426757.html,转载请注明出处] 假设我们要求解以下的最小化问题:                     ...

随机推荐

  1. reactor-core

    <dependency> <groupId>io.projectreactor</groupId> <artifactId>reactor-core&l ...

  2. oauth2 Spring Security

    oauth2四种授权方式小结 http://www.ruanyifeng.com/blog/2019/04/oauth-grant-types.html 密码模式(resource owner pas ...

  3. Windows 常用配置 - 启用长路径

    Windows 启用长路径支持 打开注册表编辑器:regedit 找到如下路径:HKEY_LOCAL_MACHINE\SYSTEM\CurrentControlSet\Control\FileSyte ...

  4. 【线段树】Interval GCD

    题目描述 给定一个长度为N的数列A,以及M条指令 (N≤5*10^5, M<=10^5),每条指令可能是以下两种之一: "C l r d",表示把 A[l],A[l+1],- ...

  5. Uncaught (in promise) NavigationDuplicated {_name: "NavigationDuplicated"}的解决方法

    左侧菜单栏时,发现点击路由跳转相同地址 会有这个报错 Uncaught (in promise) NavigationDuplicated {_name: "NavigationDuplic ...

  6. OpenSSL EVP_Digest系列函数的一个样例

    #include <stdio.h>     #include <openssl/evp.h>         main(int argc, char *argv[])     ...

  7. drf中的请求模块和渲染模块

    请求模块:request对象 APIView request.py # 在rest_framework.request.Request实例化方法中 self._request = request 将原 ...

  8. mysql，user表中各字段的含义

    1.查询user表 select * from mysql.user 2.修改用户密码 ALTER user ' 3.user表中各字段的含义 Select_priv:用户可以通过SELECT命令选择 ...

  9. Excel-DNA项目只用1个文件实现Ribbon CustomUI和CustomTaskpane定制【C#版】

    Excel-DNA项目中的自定义功能区和自定义任务窗格需要用到各种命名空间.添加所需文件,才能实现.后来我发现可以把所有代码都写在Class1.cs这个默认文件中. 大家可以在Visual Studi ...

  10. ionic2踩坑之订阅发布模式的实现

    原文地址:http://www.cnblogs.com/eccainiao/p/6429536.html 转载请说明. 在ionic2中实现订阅发布模式,需要用到Events. Events下面有三个 ...