objectarx 填充的分割

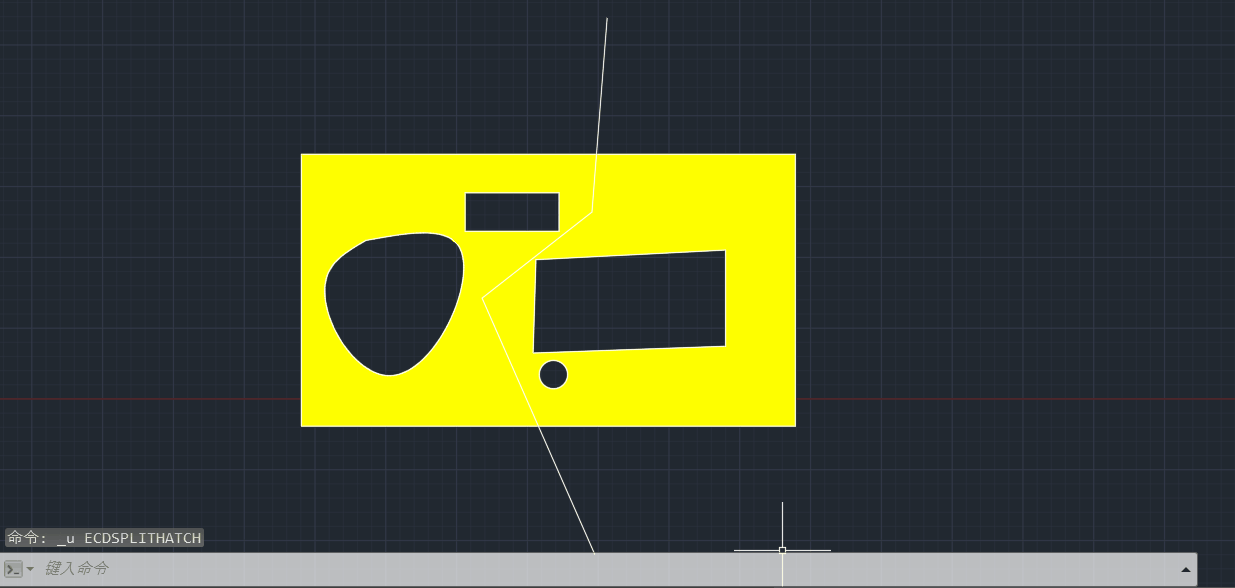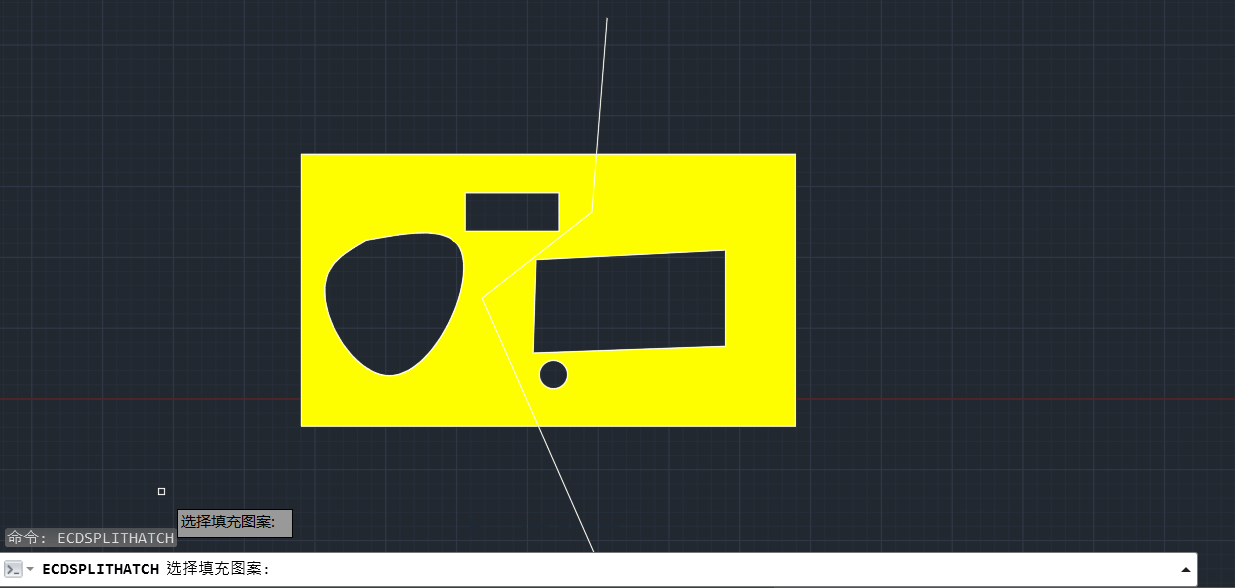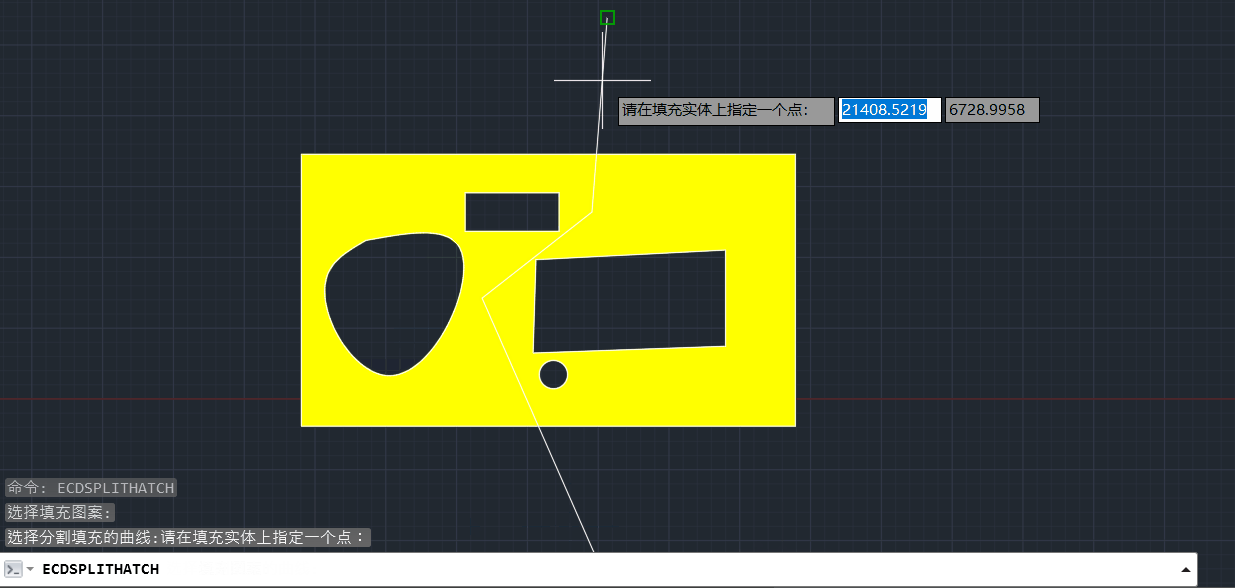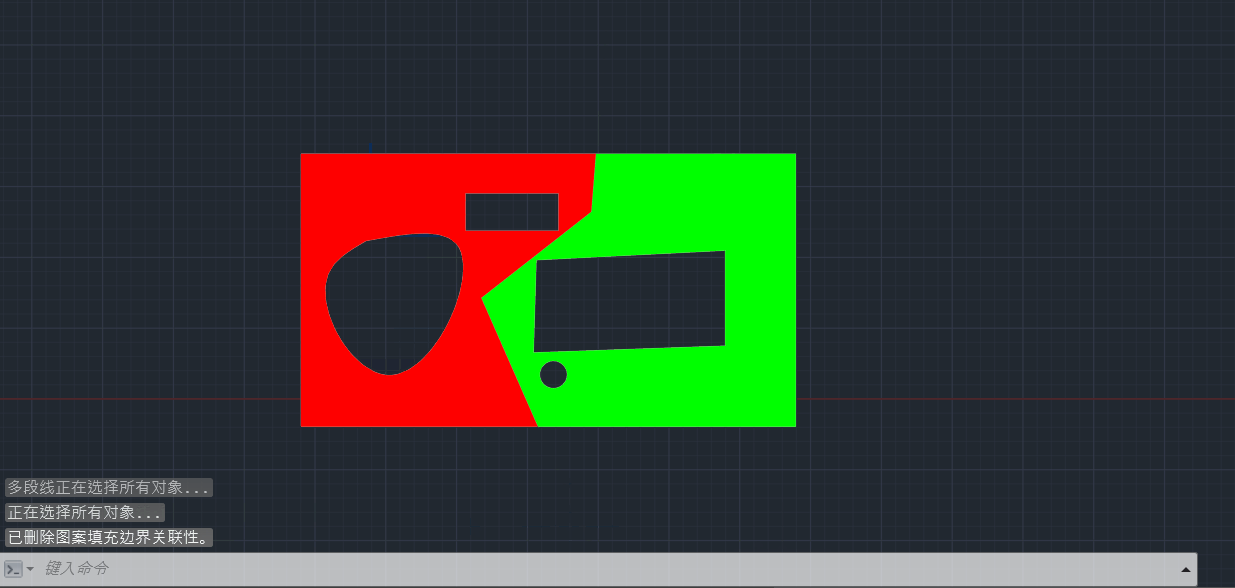
主要思路：找到填充边界集合：vecBo，然后把面积最大的边界找出来：bo1，用分割曲线和bo1通过boundary命令构成两个新的最大封闭边界，左边的记为 boLeft（红色部分），右边的记为boRight（绿色部分），在vecBo边界集合分开为：boLeft内部的边界，和boRight内部的边界。这样在分别填充的时候，就能有正确的填充边界集合。

下面放出代码：
通过选择填充求得填充边界集合：

static void GetHatchBo(AcDbHatch *pHatch,vector<AcDbEntity*>&vecBo)
    {
        Acad::ErrorStatus es;

        Adesk::Int32 LoopType;

        AcGeVoidPointerArray edgeptrAry;
        AcGeIntArray edgeTypesAry;

        AcGePoint2dArray vertices;
        AcGeDoubleArray bulges;

        //获得填充边界的数目
        int LoopNum = pHatch->numLoops();

        for (int i = ; i < LoopNum; i++)
        {
            //获取边界类型
            LoopType = pHatch->loopTypeAt(i);
            //如果边界是多义线
            if (LoopType & AcDbHatch::kPolyline)
            {
                //取得边界定义数据(polyline)的顶点数组和凸度数组，它们是一一对应的
                es = pHatch->getLoopAt(i, LoopType, vertices, bulges);
                acutPrintf(L"\n多段线");
                //是不是根据这些顶点数组和凸度数组构造一条AcDb多义线取决于你
                AcDbPolyline *pl = new AcDbPolyline();

                GetPolyline(vertices, bulges, pl);

                vecBo.push_back(pl);
            }
            else
            {
                //几乎可以取得除polyline外的所有边界定义数据
                //第三个参数返回值是无值指针数组
                //第四个参数返回值是组成边界的每一条边的类型
                //它们也是一一对应的关系
                es = pHatch->getLoopAt(i, LoopType, edgeptrAry, edgeTypesAry);

                //遍历，因为每一条边界又可能由多种AcGe曲线构成
                for (int j = ; j < edgeTypesAry.length(); j++)
                {

                    if (edgeTypesAry[j] == AcDbHatch::kLine)//直线
                    {
                        AcGeLineSeg2d *LnSeg = (AcGeLineSeg2d *)edgeptrAry[j];
                        acutPrintf(L"\n直线");
                        AcGePoint2d pt1 = LnSeg->startPoint();
                        AcGePoint2d pt2 = LnSeg->endPoint();

                        AcDbLine *line = new AcDbLine(AcGePoint3d(pt1.x,pt1.y,), AcGePoint3d(pt2.x, pt2.y, ));

                        vecBo.push_back(line);
                    }
                    //圆弧
                    else if (edgeTypesAry[j] == AcDbHatch::kCirArc)
                    {
                        AcGeCircArc2d *cirArc = (AcGeCircArc2d *)edgeptrAry[j];
                        acutPrintf(L"\n圆弧");
                        //可以根据数学圆弧构造相应的AcDb圆弧，取决于你（以下同）
                        AcGePoint2d center = cirArc->center();
                        double ra = cirArc->radius();
                        double angle1 = cirArc->startAng();
                        double angle2 = cirArc->endAng();
                        AcDbCircle *cir = new AcDbCircle(AcGePoint3d(center.x, center.y, ), AcGeVector3d::kZAxis, ra);

                        vecBo.push_back(cir);

                    }
                    else if (edgeTypesAry[j] == AcDbHatch::kEllArc)//椭圆弧
                    {
                        AcGeEllipArc2d *ellArc = (AcGeEllipArc2d *)edgeptrAry[j];
                        acutPrintf(L"\n椭圆弧");

                        AcGePoint2d center = ellArc->center();
                        AcGeVector2d majorVec = ellArc->majorAxis();
                        double angle1 = ellArc->startAng();
                        double angle2 = ellArc->endAng();
                        double rad = ellArc->majorRadius();
                        double rad2 = ellArc->minorRadius();

                        AcDbEllipse *ell = new AcDbEllipse(AcGePoint3d(center.x, center.y, ),
                            AcGeVector3d::kZAxis, AcGeVector3d(majorVec.x,majorVec.y,), rad / rad2, angle1, angle2);
                        vecBo.push_back(ell);
                    }
                    else if (edgeTypesAry[j] == AcDbHatch::kSpline)//NURBS曲线
                    {
                        AcGeNurbCurve2d *spline = (AcGeNurbCurve2d *)edgeptrAry[j];
                        acutPrintf(L"\nNURBS曲线");

                        AcDbSpline * spl = NULL;

                        createSpline(*spline, spl, );

                        vecBo.push_back(spl);

                    }
                }
            }

            vertices.removeAll();
            bulges.removeAll();
            edgeptrAry.removeAll();
            edgeTypesAry.removeAll();
        }
    }

获得填充边界集合

分割曲线构造新多段线：

if (pEnt2->isA() == AcDbPolyline::desc()) {

            AcDbPolyline * plTemp = AcDbPolyline::cast(pEnt2);

            AcGeDoubleArray dbArr;
            AcGePoint2dArray pt2dArr;

            int indexS = , indexE = ;

            GetCollOfPl(plTemp, dbArr, pt2dArr);
            //获得两个交点的索引用来构造新的多段线
            GetIndexOfPl(plTemp, pt2dArr, ptArr, indexS, indexE);

            AcDbPolyline *newPl = new AcDbPolyline();

            newPl->addVertexAt(newPl->numVerts(), AcGePoint2d(ptArr[].x, ptArr[].y), , , );

            for (int i=indexS;i<=indexE;i++)
            {
                newPl->addVertexAt(newPl->numVerts(), pt2dArr[i], dbArr[i], , );

            }
            newPl->addVertexAt(newPl->numVerts(), AcGePoint2d(ptArr[].x, ptArr[].y), , , );

            newPl->setColorIndex();

            PostToModelSpace(newPl);

            newPl->close();

        }

截取分隔曲线

构造左右边界：红色部分最大边界和绿色部分最大边界

static bool  GetBoundary(const AcGePoint3d & seedPoint, AcDbVoidPtrArray& ptrArr)
    {

        ErrorStatus es = acedTraceBoundary(seedPoint, false, ptrArr);

        if (es != Acad::eOk) {
            acutPrintf(L"\nboundary=%d", es);
            return false;
        }
        return true;
    }

判断vecBo边界集合的边界是否在左右边界内部：
主要是获得内部图形的点集，然后把左边边界内部的一点分别与这个点集中的点构成直线，如果直线和左边边界相交时有1个以上交点，就说明这个边界不在左边界内部。

static bool JudgeXj(CONST AcGePoint3dArray & ptArr, AcDbEntity *pEnt,const AcGePoint3d &innerPt) {

        AcDbLine * l = new AcDbLine();

        l->setStartPoint(innerPt);

        AcGePoint3dArray ptTemp;

        for (int i = ; i < ptArr.length(); i++)
        {
            l->setEndPoint(ptArr[i]);

            l->intersectWith(pEnt, AcDb::kOnBothOperands, ptTemp);

            if (ptTemp.length() >= ) {

                delete l;
                l = NULL;

                return true;
            }
        }
        return false;
    }

判断边界是否在左边边界内部

完整代码见附件：

https://files.cnblogs.com/files/HelloQLQ/ECDFillHatch.7z