第八篇：支持向量机 (SVM)分类器原理分析与基本应用

前言

支持向量机，也即SVM，号称分类算法，甚至机器学习界老大哥。其理论优美，发展相对完善，是非常受到推崇的算法。

本文将讲解的SVM基于一种最流行的实现 - 序列最小优化，也即SMO。

另外还将讲解将SVM扩展到非线性可分的数据集上的大致方法。

预备术语

1. 分割超平面：就是决策边界

2. 间隔：样本点到分割超平面的距离

3. 支持向量：离分割超平面距离最近的样本点

算法原理

在前一篇文章 - 逻辑回归中，讲到了通过拟合直线来进行分类。

而拟合的中心思路是求错误估计函数取得最小值，得到的拟合直线是到各样本点距离和最小的那条直线。

然而，这样的做法很多时候未必是最合适的。

请看下图：

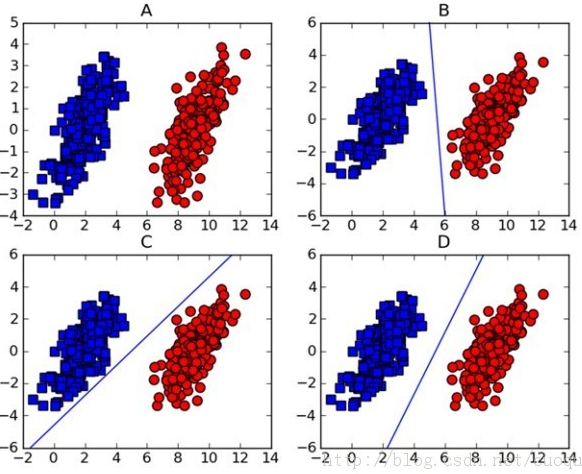
一般来说，逻辑回归得到的直线线段会是B或者C这样的形式。而很显然，从分类算法的健壮性来说，D才是最佳的拟合线段。

SVM分类算法就是基于此思想：找到具有最小间隔的样本点，然后拟合出一个到这些样本点距离和最大的线段/平面。

如何计算最优超平面

1. 首先根据算法思想 - "找到具有最小间隔的样本点，然后拟合出一个到这些样本点距离和最大的线段/平面。" 写出目标函数：

该式子的解就是待求的回归系数。

然而，这是一个嵌套优化问题，非常难进行直接优化求解。为了解这个式子，还需要以下步骤。

2. 不去计算内层的min优化，而是将距离值界定到一个范围 - 大于1，即最近的样本点，也即支持向量到超平面的距离为1。下图可以清楚表示这个意思：

去掉min操作，代之以界定：label * (w^Tx + b) >= 1。

3. 这样得到的式子就是一个带不等式的优化问题，可以采用拉格朗日乘子法(KKT条件)去求解。

具体步骤推论本文不给出。推导结果为：

另外，可加入松弛系数 C，用于控制 "最大化间隔" 和"保证大部分点的函数间隔小于1.0" 这两个目标的权重。

将 α >= 0 条件改为 C >= α >= 0 即可。

α 是用于求解过程中的一个向量，它和要求的结果回归系数是一一对应的关系。

将其中的 α 解出后，便可依据如下两式子(均为推导过程中出现的式子)进行转换得到回归系数：

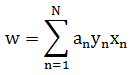
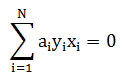
说明: 要透彻理解完整的数学推导过程需要一些时间，可参考某位大牛的文章http://blog.csdn.net/v_july_v/article/details/7624837。

使用SMO - 高效优化算法求解 α 值

算法思想：

每次循环中选择两个 α 进行优化处理。一旦找到一对合适的 α，那么就增大其中一个减小另外一个。

所谓合适，是指必须符合两个条件：1. 两个 α 值必须要在 α 分隔边界之外 2. 这两个α 还没有进行过区间化处理或者不在边界上。

使用SMO求解 α 伪代码：

 创建一个 alpha 向量并将其初始化为全0
 当迭代次数小于最大迭代次数(外循环):
     对数据集中的每个向量(内循环):
         如果该数据向量可以被优化
         随机选择另外一个数据向量
         同时优化这两个向量
         如果都不能被优化，推出内循环。
     如果所有向量都没有被优化，则增加迭代数目，继续下一次的循环。

实现及测试代码：

 #!/usr/bin/env python
 # -*- coding:UTF-8 -*-

 '''
 Created on 20**-**-**

 @author: fangmeng
 '''

 from numpy import *
 from time import sleep

 #=====================================
 # 输入：
 #        fileName: 数据文件
 # 输出:
 #        dataMat: 测试数据集
 #        labelMat: 测试分类标签集
 #=====================================
 def loadDataSet(fileName):
     '载入数据'

     dataMat = []; labelMat = []
     fr = open(fileName)
     for line in fr.readlines():
         lineArr = line.strip().split('\t')
         dataMat.append([float(lineArr[0]), float(lineArr[1])])
         labelMat.append(float(lineArr[2]))
     return dataMat,labelMat

 #=====================================
 # 输入：
 #        i: 返回结果不等于该参数
 #        m: 指定随机范围的参数
 # 输出:
 #        j: 0-m内不等于i的一个随机数
 #=====================================
 def selectJrand(i,m):
     '随机取数'

     j=i
     while (j==i):
         j = int(random.uniform(0,m))
     return j

 #=====================================
 # 输入：
 #        aj: 数据对象
 #        H: 数据对象最大值
 #        L: 数据对象最小值
 # 输出:
 #        aj: 定界后的数据对象。最大H 最小L
 #=====================================
 def clipAlpha(aj,H,L):
     '为aj定界'

     if aj > H:
         aj = H
     if L > aj:
         aj = L
     return aj

 #=====================================
 # 输入：
 #        dataMatIn: 数据集
 #        classLabels: 分类标签集
 #        C: 松弛参数
 #        toler: 荣错率
 #        maxIter: 最大循环次数
 # 输出:
 #        b: 偏移
 #        alphas: 拉格朗日对偶因子
 #=====================================
 def smoSimple(dataMatIn, classLabels, C, toler, maxIter):
     'SMO算法求解alpha'

     # 数据格式转化
     dataMatrix = mat(dataMatIn);
     labelMat = mat(classLabels).transpose()
     m,n = shape(dataMatrix)
     alphas = mat(zeros((m,1)))

     iter = 0
     b = 0
     while (iter < maxIter):
         # alpha 改变标记
         alphaPairsChanged = 0

         # 对所有数据集
         for i in range(m):
             # 预测结果
             fXi = float(multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[i,:].T)) + b
             # 预测结果与实际的差值
             Ei = fXi - float(labelMat[i])
             # 如果差值太大则进行优化
             if ((labelMat[i]*Ei < -toler) and (alphas[i] < C)) or ((labelMat[i]*Ei > toler) and (alphas[i] > 0)):
                 # 随机选择另外一个样本
                 j = selectJrand(i,m)
                 # 计算另外一个样本的预测结果以及差值
                 fXj = float(multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[j,:].T)) + b
                 Ej = fXj - float(labelMat[j])
                 # 暂存当前alpha值对
                 alphaIold = alphas[i].copy();
                 alphaJold = alphas[j].copy();
                 # 确定alpha的最大最小值
                 if (labelMat[i] != labelMat[j]):
                     L = max(0, alphas[j] - alphas[i])
                     H = min(C, C + alphas[j] - alphas[i])
                 else:
                     L = max(0, alphas[j] + alphas[i] - C)
                     H = min(C, alphas[j] + alphas[i])
                 if L==H:
                     pass
                 # eta为alphas[j]的最优修改量
                 eta = 2.0 * dataMatrix[i,:]*dataMatrix[j,:].T - dataMatrix[i,:]*dataMatrix[i,:].T - dataMatrix[j,:]*dataMatrix[j,:].T
                 if eta >= 0:
                     print "eta>=0"; continue
                 # 订正alphas[j]
                 alphas[j] -= labelMat[j]*(Ei - Ej)/eta
                 alphas[j] = clipAlpha(alphas[j],H,L)
                 # 如果alphas[j]发生了轻微变化
                 if (abs(alphas[j] - alphaJold) < 0.00001):
                     continue
                 # 订正alphas[i]
                 alphas[i] += labelMat[j]*labelMat[i]*(alphaJold - alphas[j])

                 # 订正b
                 b1 = b - Ei- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[i,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[i,:]*dataMatrix[j,:].T
                 b2 = b - Ej- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[j,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[j,:]*dataMatrix[j,:].T
                 if (0 < alphas[i]) and (C > alphas[i]): b = b1
                 elif (0 < alphas[j]) and (C > alphas[j]): b = b2
                 else: b = (b1 + b2)/2.0

                 # 更新修改标记参数
                 alphaPairsChanged += 1

         if (alphaPairsChanged == 0): iter += 1
         else: iter = 0

     return b,alphas

 def test():
     '测试'

     dataArr, labelArr = loadDataSet('/home/fangmeng/testSet.txt')
     b, alphas = smoSimple(dataArr, labelArr, 0.6, 0.001, 40)
     print b
     print alphas[alphas>0]

 if __name__ == '__main__':
     test()

其中，testSet.txt数据文件格式为三列，前两列特征，最后一列分类结果。

测试结果：

结果具有随机性，多次运行的结果不一定一致。

得到 alphas 数组和 b 向量就能直接算到回归系数了，参考上述代码 93 行，稍作变换即可。

非线性可分情况的大致解决思路

当数据分析图类似如下的情况：

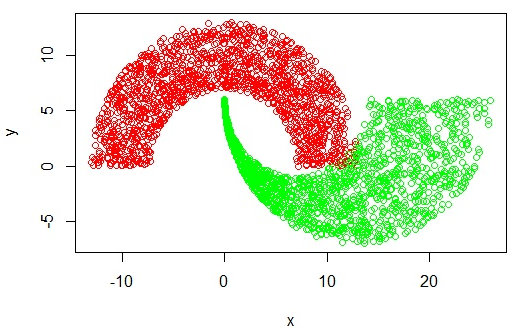
则显然无法拟合出一条直线来。碰到这种情况的解决办法是使用核函数 - 将在低维处理非线性问题转换为在高维处理线性问题。

也就是说，将在SMO中所有出现了向量内积的地方都替换成核函数处理。

具体的用法，代码本文不做讲解。

小结

支持向量机是分类算法中目前用的最多的，也是最为完善的。

关于支持向量机的讨论远远不会止于此，本文初衷仅仅是对这个算法有一定的了解，认识。

若是在以后的工作中需要用到这方面的知识，还需要全面深入的学习，研究。