频分复用（Frequency Division Multiplexer）

作者：桂。

时间：2017年12月19日20:43:04

链接：http://www.cnblogs.com/xingshansi/p/8067839.html

---

前言

主要记录基本的频分复用原理，以及仿真实现。

一、频分复用原理

频分复用FDM:

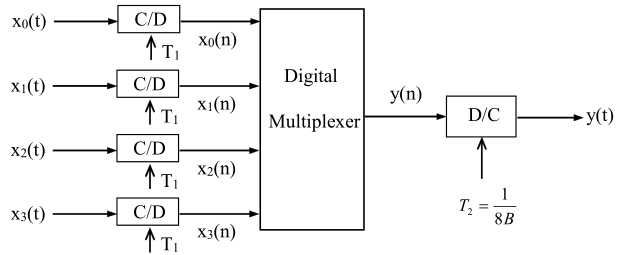
通常x1..4(t)可以是同一个序列的串并转化，也可以是不同序列，频分复用示意图：

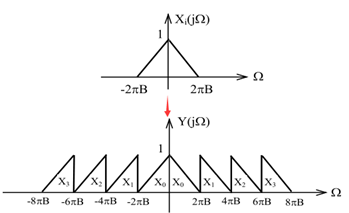
主要包含三个操作：1）上采样(up-sample); 2）滤波（fir）;3）累加(sum)。

频分复用：将多个不同频段的信号拼接为一个宽带信号，主要包含三个操作：1）上采样(up-sample); 2）滤波（fir）;3）累加(sum)。

• 上采样

T₁/T₂ = 4，故上采样倍数为4，上采样有原数据保持、插值、补零等方法，这里采用最基本的补零方法。不失一般性，X₀(n)、X₁(n)、X₂(n)、X₃(n)分别按不同频率的正弦信号处理。

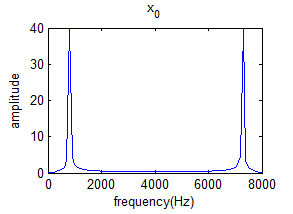
以x₁(n) 的频域变换：

4倍插值后的频谱：

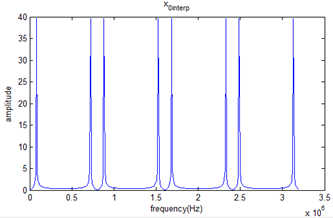
可以看出插值后出现了多个重复周期，因此需要借助低通滤波以保留单一周期，如下图所示:

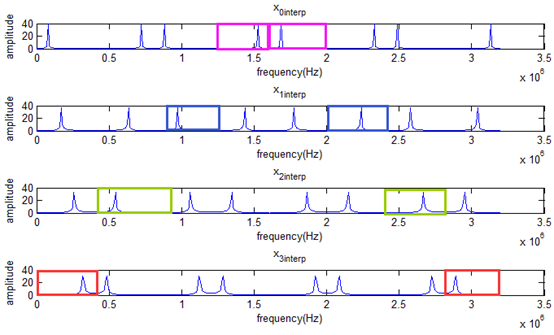
因此需要构造不同频段的滤波器，四个蓝色阴影部分拼接（累加）即可。

• 滤波器

这里prototype滤波器:

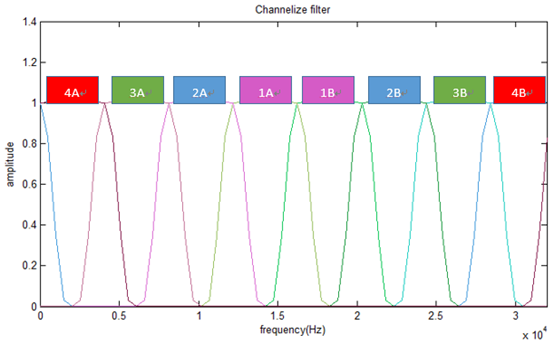
共构造8个滤波器，分成四组，输出y(n)为：

Y(n) = y0(n)+ y1(n)+ y2(n)+ y3(n)

y_m(n)：

Y_m(n) = xm_interpl(n)*[h_a (n) exp((-im*2*pi*(m*n))/8)+ h_a(n) exp((-im*2*pi*((8-m)*n))/8)]

= 2*xm_interpl(n)*[h_a(n)cos((-2*pi*(m*n))/8)]

其中h_a (n) = h(n)* exp((-im*pi*n)/8)为prototype filter，至此便完成了信号的频分多路复用（FDM）理论推导.

• 累加

滤波后的各个输出累加，即得到调制的y(n)，仿真图如图所示：

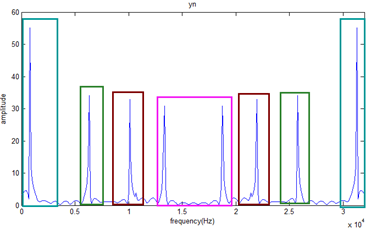
结果与上文一致。

二、仿真结果

频分复用的接收端是发射的逆过程，分别利用 基本滤波器、多相滤波器实现：

基本滤波器：

%recovery signal: x
clc;clear all;close all;
load fir2.mat;
fir = fir2;
B = 4000;%4KHz
fs1 = 2*B;
D = 4;
t1 = 0:1/fs1:(128-1)/fs1;
f = [800 1600 2200 2800];%frequency
x0 = sin(2*pi*t1*f(1));
x1 = sin(2*pi*t1*f(2));
x2 = sin(2*pi*t1*f(3));
x3 = sin(2*pi*t1*f(4));
x_shape = [x0;x1;x2;x3];
%% interp
x0_interp = [x0;zeros(3,length(t1))];
x0_interp = x0_interp(:)';
x1_interp = [x1;zeros(3,length(t1))];
x1_interp = x1_interp(:)';
x2_interp = [x2;zeros(3,length(t1))];
x2_interp = x2_interp(:)';
x3_interp = [x3;zeros(3,length(t1))];
x3_interp = x3_interp(:)';
%%prototype filter
x_all = [x0_interp;x1_interp;x2_interp;x3_interp;flipud([x0_interp;x1_interp;x2_interp;x3_interp])];
im = sqrt(-1);
iseq = 1:length(fir);
for j = 1:D
        h_channel(j,:) = fir.*cos((2*pi*((j-1/2)*(iseq-1)))/8);
%     h_channel(j,:) = fir.*exp((1j*2*pi*((j-1/2)*(iseq-1)))/8);
end
%%add signal
yn = zeros(1,length(x3_interp));
for i = 1:D
    yn = filter(h_channel(i,:),1,x_all(i,:))+yn;
end
%%demultiplex
x_channel = zeros(D,length(yn)/D);
for i = 1:D
    x_channel(i,:) = downsample(filter(h_channel(i,:),1,yn),D);
end
figure()
for i = 1:D
    subplot(2,2,i)
    plot(linspace(0,fs1,length(t1)),abs(fft(x_channel(i,:))));
    xlabel('frequency(Hz)');ylabel('amplitude');title('direct filter -> x');
end

%%plot mse
figure()
for i = 1:4
     x_channel(i,:) =  x_channel(i,:)/max(abs( x_channel(i,:)));
     subplot (2,2,i)
     plot(linspace(0,fs1,length(t1)),x_channel(i,:));hold on;
     plot(linspace(0,fs1,length(t1)),x_shape(i,:),'r--');hold on;
%      plot(linspace(0,fs1,length(t1)),abs(x_shape(i,:)-x_channel(i,:)).^2,'k');
     xlabel('frequency(Hz)');title('MSE');
%      legend('recovery','orignal','MSE');
end

　　多相滤波器，推导：

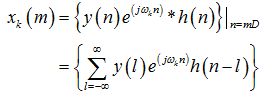
令l = iD+p，D表示分解后信号路数，此处D = 4:

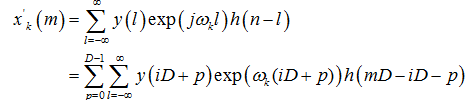
令，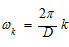

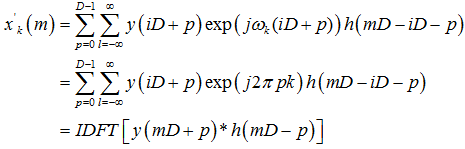
再将结果取实部即可得解。

%recovery signal by polyphase filter: x
clc;clear all;close all;
load fir2.mat;
fir = fir2;
B = 4000;%4KHz
fs1 = 2*B;
D = 4;
t1 = 0:1/fs1:(128-1)/fs1;
f = [800 1600 2200 2800];%frequency
x0 = sin(2*pi*t1*f(1));
x1 = sin(2*pi*t1*f(2));
x2 = sin(2*pi*t1*f(3));
x3 = sin(2*pi*t1*f(4));
x_shape = [x0;x1;x2;x3];
%% interp
x0_interp = [x0;zeros(3,length(t1))];
x0_interp = x0_interp(:)';
x1_interp = [x1;zeros(3,length(t1))];
x1_interp = x1_interp(:)';
x2_interp = [x2;zeros(3,length(t1))];
x2_interp = x2_interp(:)';
x3_interp = [x3;zeros(3,length(t1))];
x3_interp = x3_interp(:)';
%%prototype filter
x_all = [x0_interp;x1_interp;x2_interp;x3_interp;flipud([x0_interp;x1_interp;x2_interp;x3_interp])];
im = sqrt(-1);
iseq = 1:length(fir);
for j = 1:D
        h_channel(j,:) = fir.*cos((-2*pi*((j-1/2)*(iseq-1)))/8);
%     h_channel(j,:) = fir.*exp((1j*2*pi*((j-1/2)*(iseq-1)))/8);
end
%%add signal
yn = zeros(1,length(x3_interp));
for i = 1:D
    yn = filter(h_channel(i,:),1,x_all(i,:))+yn;
end
%%demultiplex
%prototype filter
h0 = fir.*exp((-1j*2*pi*((-1/2)*(iseq-1)))/8);
h_py = fliplr(reshape(h0,D,length(h0)/D));
y_py = (reshape(yn,D,length(yn)/D));
x_channel = zeros(D,length(yn)/D);
for i = 1:D
    x_channel(i,:) = filter(h_py(i,:),1,y_py(i,:));
end
x_channel = real(ifft(x_channel));
x_channel = x_channel([1,4,2,3],:);
%%plot mse
figure()
for i = 1:4
     x_channel(i,:) =  x_channel(i,:)/max(abs( x_channel(i,:)));
     subplot (2,2,i)
     plot(linspace(0,fs1,length(t1)),x_channel(i,:));hold on;
     plot(linspace(0,fs1,length(t1)),x_shape(i,:),'r--');hold on;
%      plot(linspace(0,fs1,length(t1)),abs(x_shape(i,:)-x_channel(i,:)).^2,'k');
     xlabel('frequency(Hz)');title('MSE');
%      legend('recovery','orignal','MSE');
end

三、其他

原型滤波器信道化思路：

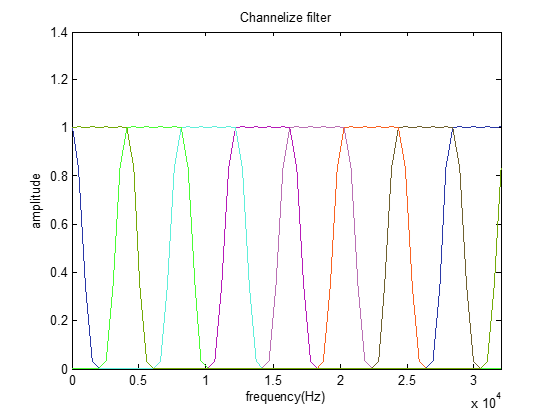
信道化与频分复用略有不同，频分复用主要是余弦函数，理论上相邻无衰减，得到的余弦曲线并不理想：

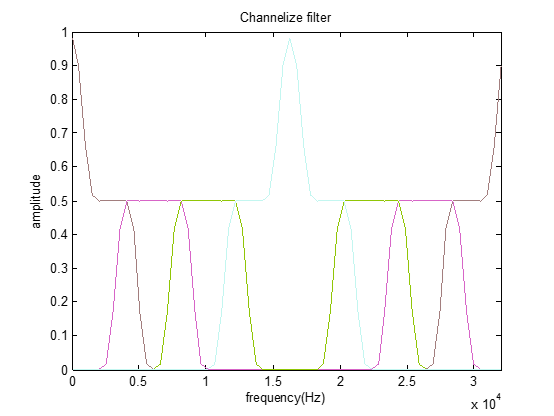
当有一定的过渡带时，余弦曲线：

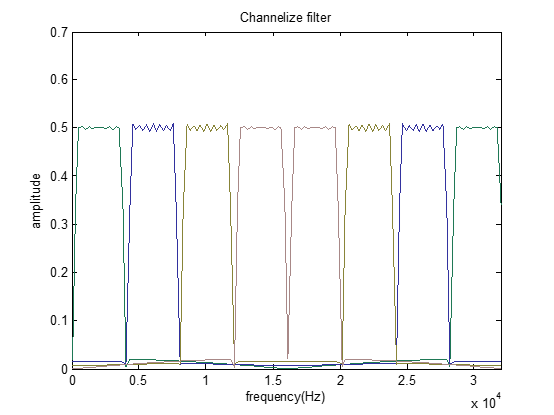
可见此时应该有一个过渡带才更加合理，而不是像信道化体系常用的约束：相邻信道无缝连接。