tensorflow中常用学习率更新策略

神经网络训练过程中，根据每batch训练数据前向传播的结果，计算损失函数，再由损失函数根据梯度下降法更新每一个网络参数，在参数更新过程中使用到一个学习率（learning rate），用来定义每次参数更新的幅度。

过小的学习率会降低网络优化的速度，增加训练时间，过大的学习率可能导致网络参数在最终的极优值两侧来回摆动，导致网络不能收敛。实践中证明有效的方法是设置一个根据迭代次数衰减的学习率，可以兼顾训练效率和后期的稳定性。

分段常数衰减

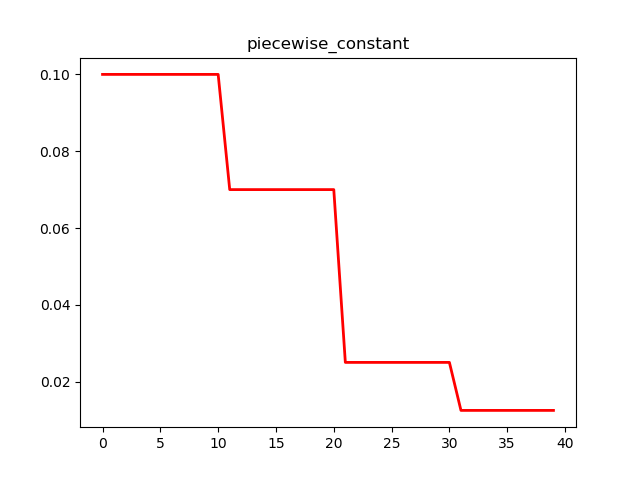
分段常数衰减是在事先定义好的训练次数区间上，设置不同的学习率常数。刚开始学习率大一些，之后越来越小，区间的设置需要根据样本量调整，一般样本量越大区间间隔应该越小。

tf中定义了tf.train.piecewise_constant 函数，实现了学习率的分段常数衰减功能。

tf.train.piecewise_constant(

    x,

    boundaries,

    values,

    name=None

)

x: 标量，指代训练次数
boundaries：学习率参数应用区间列表
values：学习率列表，values的长度比boundaries的长度多一个
name：操作的名称

# coding:utf-8

import matplotlib.pyplot as plt

import tensorflow as tf

num_epoch = tf.Variable(0, name='global_step', trainable=False)

boundaries = [10, 20, 30]

learing_rates = [0.1, 0.07, 0.025, 0.0125]

y = []

N = 40

with tf.Session() as sess:

    sess.run(tf.global_variables_initializer())

    for num_epoch in range(N):

        learing_rate = tf.train.piecewise_constant(num_epoch, boundaries=boundaries, values=learing_rates)

        lr = sess.run([learing_rate])

        y.append(lr)

x = range(N)

plt.plot(x, y, 'r-', linewidth=2)

plt.title('piecewise_constant')

plt.show()

分段常数衰减可以让调试人员针对不同任务设置不同的学习率，进行精细调参，要求调试人员对模型和数据集有深刻认识，要求较高。

指数衰减

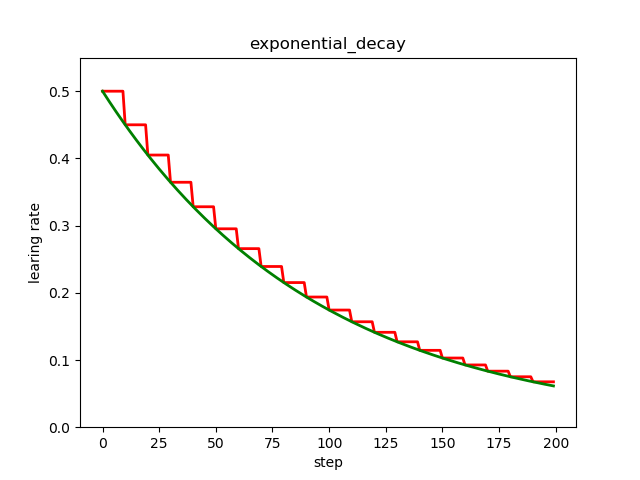
指数衰减是比较常用的衰减方法，学习率是跟当前的训练轮次指数相关的。

tf中实现指数衰减的函数是 tf.train.exponential_decay()。

tf.train.exponential_decay(

    learning_rate,

    global_step,

    decay_steps,

    decay_rate,

    staircase=False,

    name=None

)

learning_rate: 初始学习率
global_step: 当前训练轮次，epoch
decay_step: 定义衰减周期，跟参数staircase配合，可以在decay_step个训练轮次内保持学习率不变
decay_rate，衰减率系数
staircase：定义是否是阶梯型衰减，还是连续衰减，默认是False，即连续衰减（标准的指数型衰减）
name：操作名称

函数返回学习率数值，计算公式是：

decayed_learning_rate = learning_rate *

                        decay_rate ^ (global_step / decay_steps)

# coding:utf-8

import matplotlib.pyplot as plt

import tensorflow as tf

num_epoch = tf.Variable(0, name='global_step', trainable=False)

y = []

z = []

N = 200

with tf.Session() as sess:

    sess.run(tf.global_variables_initializer())

    for num_epoch in range(N):

        # 阶梯型衰减

        learing_rate1 = tf.train.exponential_decay(

            learning_rate=0.5, global_step=num_epoch, decay_steps=10, decay_rate=0.9, staircase=True)

        # 标准指数型衰减

        learing_rate2 = tf.train.exponential_decay(

            learning_rate=0.5, global_step=num_epoch, decay_steps=10, decay_rate=0.9, staircase=False)

        lr1 = sess.run([learing_rate1])

        lr2 = sess.run([learing_rate2])

        y.append(lr1)

        z.append(lr2)

x = range(N)

fig = plt.figure()

ax = fig.add_subplot(111)

ax.set_ylim([0, 0.55])

plt.plot(x, y, 'r-', linewidth=2)

plt.plot(x, z, 'g-', linewidth=2)

plt.title('exponential_decay')

ax.set_xlabel('step')

ax.set_ylabel('learing rate')

plt.show()

红色的是阶梯型指数衰减，在一定轮次内学习率保持一致，绿色的是标准的指数衰减，即连续型指数衰减。

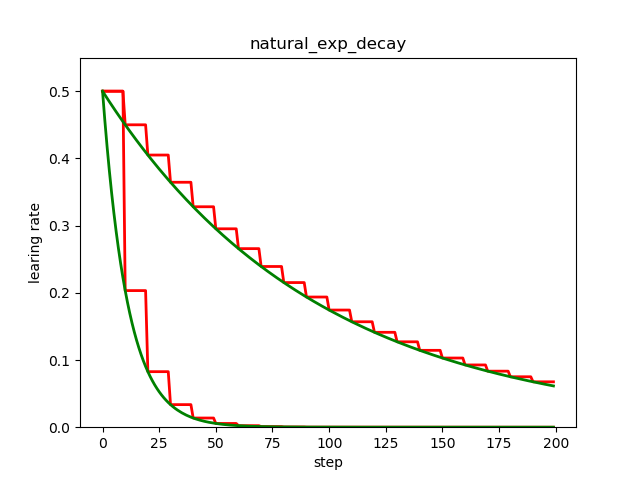
自然指数衰减

自然指数衰减是指数衰减的一种特殊情况，学习率也是跟当前的训练轮次指数相关，只不过以 e 为底数。

tf中实现自然指数衰减的函数是 tf.train.natural_exp_decay()

tf.train.natural_exp_decay(

    learning_rate,

    global_step,

    decay_steps,

    decay_rate,

    staircase=False,

    name=None

)

learning_rate: 初始学习率
global_step: 当前训练轮次，epoch
decay_step: 定义衰减周期，跟参数staircase配合，可以在decay_step个训练轮次内保持学习率不变
decay_rate，衰减率系数
staircase：定义是否是阶梯型衰减，还是连续衰减，默认是False，即连续衰减（标准的指数型衰减）
name：操作名称

自然指数衰减的计算公式是：

decayed_learning_rate = learning_rate * exp(-decay_rate * global_step)

# coding:utf-8

import matplotlib.pyplot as plt

import tensorflow as tf

num_epoch = tf.Variable(0, name='global_step', trainable=False)

y = []

z = []

w = []

m = []

N = 200

with tf.Session() as sess:

    sess.run(tf.global_variables_initializer())

    for num_epoch in range(N):

        # 阶梯型衰减

        learing_rate1 = tf.train.natural_exp_decay(

            learning_rate=0.5, global_step=num_epoch, decay_steps=10, decay_rate=0.9, staircase=True)

        # 标准指数型衰减

        learing_rate2 = tf.train.natural_exp_decay(

            learning_rate=0.5, global_step=num_epoch, decay_steps=10, decay_rate=0.9, staircase=False)

        # 阶梯型指数衰减

        learing_rate3 = tf.train.exponential_decay(

            learning_rate=0.5, global_step=num_epoch, decay_steps=10, decay_rate=0.9, staircase=True)

        # 标准指数衰减

        learing_rate4 = tf.train.exponential_decay(

            learning_rate=0.5, global_step=num_epoch, decay_steps=10, decay_rate=0.9, staircase=False)

        lr1 = sess.run([learing_rate1])

        lr2 = sess.run([learing_rate2])

        lr3 = sess.run([learing_rate3])

        lr4 = sess.run([learing_rate4])

        y.append(lr1)

        z.append(lr2)

        w.append(lr3)

        m.append(lr4)

x = range(N)

fig = plt.figure()

ax = fig.add_subplot(111)

ax.set_ylim([0, 0.55])

plt.plot(x, y, 'r-', linewidth=2)

plt.plot(x, z, 'g-', linewidth=2)

plt.plot(x, w, 'r-', linewidth=2)

plt.plot(x, m, 'g-', linewidth=2)

plt.title('natural_exp_decay')

ax.set_xlabel('step')

ax.set_ylabel('learing rate')

plt.show()

左下部分的两条曲线是自然指数衰减，右上部分的两条曲线是指数衰减，可见自然指数衰减对学习率的衰减程度要远大于一般的指数衰减，一般用于可以较快收敛的网络，或者是训练数据集比较大的场合。

多项式衰减

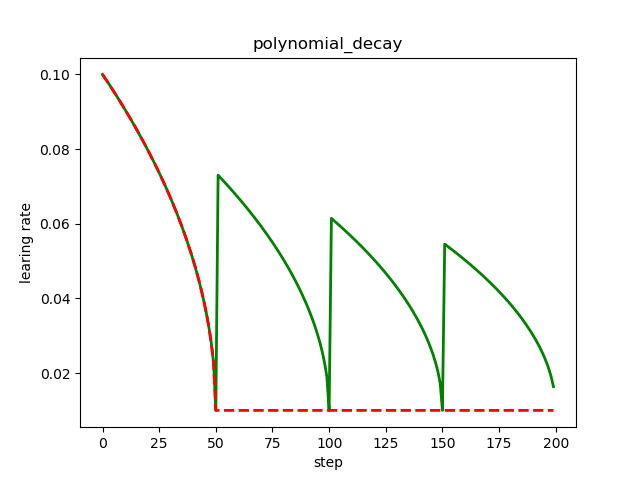
多项式衰减是这样一种衰减机制：定义一个初始的学习率，一个最低的学习率，按照设置的衰减规则，学习率从初始学习率逐渐降低到最低的学习率，并且可以定义学习率降低到最低的学习率之后，是一直保持使用这个最低的学习率，还是到达最低的学习率之后再升高学习率到一定值，然后再降低到最低的学习率（反复这个过程）。

tf中实现多项式衰减的函数是 tf.train.polynomial_decay()

tf.train.polynomial_decay(

    learning_rate,

    global_step,

    decay_steps,

    end_learning_rate=0.0001,

    power=1.0,

    cycle=False,

    name=None

)

learning_rate: 初始学习率
global_step: 当前训练轮次，epoch
decay_step: 定义衰减周期
end_learning_rate：最小的学习率，默认值是0.0001
power：多项式的幂，默认值是1,即线性的
cycle：定义学习率是否到达最低学习率后升高，然后再降低，默认False，保持最低学习率
name：操作名称

多项式衰减的学习率计算公式：

global_step = min(global_step, decay_steps)

decayed_learning_rate = (learning_rate - end_learning_rate) *

                        (1 - global_step / decay_steps) ^ (power) +

                        end_learning_rate

如果定义 cycle为True，学习率在到达最低学习率后往复升高降低，此时学习率计算公式为：

decay_steps = decay_steps * ceil(global_step / decay_steps)

decayed_learning_rate = (learning_rate - end_learning_rate) *

                        (1 - global_step / decay_steps) ^ (power) +

                        end_learning_rate

# coding:utf-8

import matplotlib.pyplot as plt

import tensorflow as tf

y = []

z = []

N = 200

global_step = tf.Variable(0, name='global_step', trainable=False)

with tf.Session() as sess:

    sess.run(tf.global_variables_initializer())

    for global_step in range(N):

        # cycle=False

        learing_rate1 = tf.train.polynomial_decay(

            learning_rate=0.1, global_step=global_step, decay_steps=50,

            end_learning_rate=0.01, power=0.5, cycle=False)

        # cycle=True

        learing_rate2 = tf.train.polynomial_decay(

            learning_rate=0.1, global_step=global_step, decay_steps=50,

            end_learning_rate=0.01, power=0.5, cycle=True)

        lr1 = sess.run([learing_rate1])

        lr2 = sess.run([learing_rate2])

        y.append(lr1)

        z.append(lr2)

x = range(N)

fig = plt.figure()

ax = fig.add_subplot(111)

plt.plot(x, z, 'g-', linewidth=2)

plt.plot(x, y, 'r--', linewidth=2)

plt.title('polynomial_decay')

ax.set_xlabel('step')

ax.set_ylabel('learing rate')

plt.show()

红色的学习率衰减曲线对应 cycle = False，下降后不再上升，保持不变，绿色的学习率衰减曲线对应 cycle = True，下降后往复升降。

多项式衰减中设置学习率可以往复升降的目的是为了防止神经网络后期训练的学习率过小，导致网络参数陷入某个局部最优解出不来，设置学习率升高机制，有可能使网络跳出局部最优解。

余弦衰减

余弦衰减的衰减机制跟余弦函数相关，形状也大体上是余弦形状。tf中的实现函数是:

tf.train.cosine_decay()

tf.train.cosine_decay(

    learning_rate,

    global_step,

    decay_steps,

    alpha=0.0,

    name=None

)

learning_rate：初始学习率
global_step: 当前训练轮次，epoch
decay_steps：衰减步数，即从初始学习率衰减到最小学习率需要的训练轮次
alpha=：最小学习率
name：操作的名称

余弦衰减学习率计算公式：

global_step = min(global_step, decay_steps)

cosine_decay = 0.5 * (1 + cos(pi * global_step / decay_steps))

decayed = (1 - alpha) * cosine_decay + alpha

decayed_learning_rate = learning_rate * decayed

改进的余弦衰减方法还有：
线性余弦衰减，对应函数 tf.train.linear_cosine_decay()
噪声线性余弦衰减，对应函数 tf.train.noisy_linear_cosine_decay()

# coding:utf-8

import matplotlib.pyplot as plt

import tensorflow as tf

y = []

z = []

w = []

N = 200

global_step = tf.Variable(0, name='global_step', trainable=False)

with tf.Session() as sess:

    sess.run(tf.global_variables_initializer())

    for global_step in range(N):

        # 余弦衰减

        learing_rate1 = tf.train.cosine_decay(

            learning_rate=0.1, global_step=global_step, decay_steps=50)

        # 线性余弦衰减

        learing_rate2 = tf.train.linear_cosine_decay(

            learning_rate=0.1, global_step=global_step, decay_steps=50,

            num_periods=0.2, alpha=0.5, beta=0.2)

        # 噪声线性余弦衰减

        learing_rate3 = tf.train.noisy_linear_cosine_decay(

            learning_rate=0.1, global_step=global_step, decay_steps=50,

            initial_variance=0.01, variance_decay=0.1, num_periods=0.2, alpha=0.5, beta=0.2)

        lr1 = sess.run([learing_rate1])

        lr2 = sess.run([learing_rate2])

        lr3 = sess.run([learing_rate3])

        y.append(lr1)

        z.append(lr2)

        w.append(lr3)

x = range(N)

fig = plt.figure()

ax = fig.add_subplot(111)

plt.plot(x, z, 'b-', linewidth=2)

plt.plot(x, y, 'r-', linewidth=2)

plt.plot(x, w, 'g-', linewidth=2)

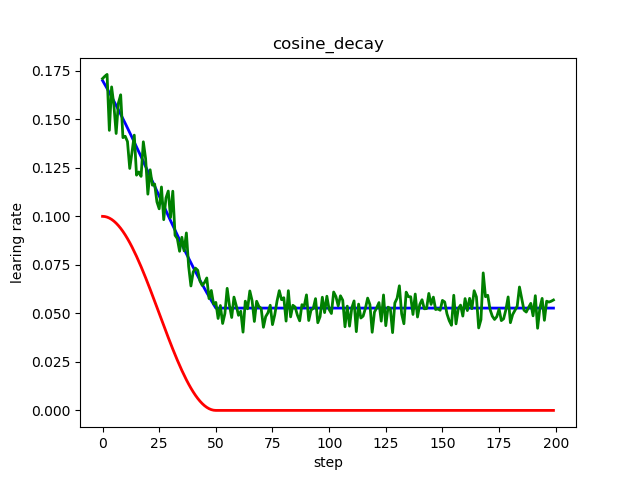
plt.title('cosine_decay')

ax.set_xlabel('step')

ax.set_ylabel('learing rate')

plt.show()

红色标准余弦衰减，学习率从初始曲线过渡到最低学习率;
蓝色线性余弦衰减，学习率从初始线性过渡到最低学习率;
绿色噪声线性余弦衰减，在线性余弦衰减基础上增加了随机噪声;

倒数衰减

倒数衰减指的是一个变量的大小与另一个变量的大小成反比的关系，具体到神经网络中就是学习率的大小跟训练次数有一定的反比关系。

tf中实现倒数衰减的函数是 tf.train.inverse_time_decay()。

tf.train.inverse_time_decay(

    learning_rate,

    global_step,

    decay_steps,

    decay_rate,

    staircase=False,

    name=None

)

learning_rate：初始学习率
global_step：用于衰减计算的全局步数
decay_steps：衰减步数
decay_rate：衰减率
staircase：是否应用离散阶梯型衰减（否则为连续型）
name：操作的名称

倒数衰减的计算公式：

decayed_learning_rate =learning_rate/(1+decay_rate* global_step/decay_step)

# coding:utf-8

import matplotlib.pyplot as plt

import tensorflow as tf

y = []

z = []

N = 200

global_step = tf.Variable(0, name='global_step', trainable=False)

with tf.Session() as sess:

    sess.run(tf.global_variables_initializer())

    for global_step in range(N):

        # 阶梯型衰减

        learing_rate1 = tf.train.inverse_time_decay(

            learning_rate=0.1, global_step=global_step, decay_steps=20,

            decay_rate=0.2, staircase=True)

        # 连续型衰减

        learing_rate2 = tf.train.inverse_time_decay(

            learning_rate=0.1, global_step=global_step, decay_steps=20,

            decay_rate=0.2, staircase=False)

        lr1 = sess.run([learing_rate1])

        lr2 = sess.run([learing_rate2])

        y.append(lr1)

        z.append(lr2)

x = range(N)

fig = plt.figure()

ax = fig.add_subplot(111)

plt.plot(x, z, 'r-', linewidth=2)

plt.plot(x, y, 'g-', linewidth=2)

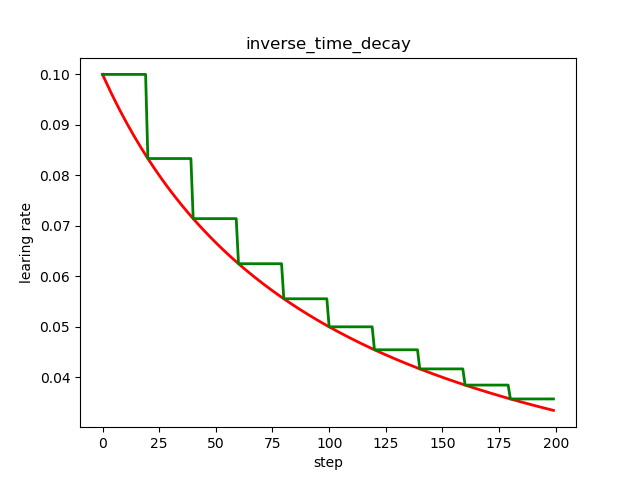
plt.title('inverse_time_decay')

ax.set_xlabel('step')

ax.set_ylabel('learing rate')

plt.show()

倒数衰减不固定最小学习率，迭代次数越多，学习率越小。