二叉查找树(二)之 C++的实现
概要
上一章介绍了"二叉查找树的相关理论知识，并通过C语言实现了二叉查找树"。这一章给出二叉查找树的C++版本。这里不再对树的相关概念进行介绍，若遇到不明白的概念，可以在上一章查找。
目录
1. 二叉树查找树
2. 二叉查找树的C++实现3. 二叉查找树的C++实现(完整源码)
4. 二叉查找树的C++测试程序
转载请注明出处：http://www.cnblogs.com/skywang12345/p/3576373.html
更多内容: 数据结构与算法系列 目录
(01) 二叉查找树(一)之 图文解析 和 C语言的实现
(02) 二叉查找树(二)之 C++的实现(03) 二叉查找树(三)之 Java的实现
二叉查找树简介
二叉查找树(Binary Search Tree)，又被称为二叉搜索树。
它是特殊的二叉树：对于二叉树，假设x为二叉树中的任意一个结点，x节点包含关键字key，节点x的key值记为key[x]。如果y是x的左子树中的一个结点，则key[y] <= key[x]；如果y是x的右子树的一个结点，则key[y] >= key[x]。那么，这棵树就是二叉查找树。如下图所示：
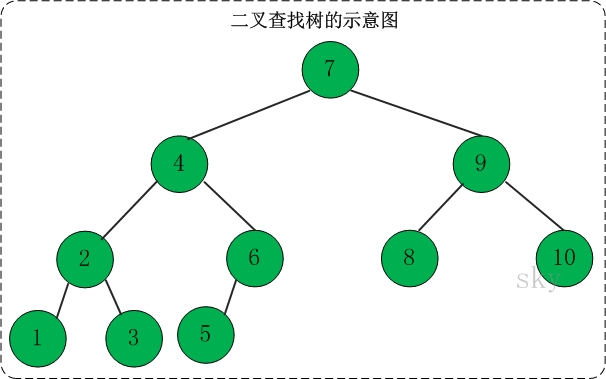
在二叉查找树中：
(01) 若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
(02) 任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
(03) 任意节点的左、右子树也分别为二叉查找树。
(04) 没有键值相等的节点（no duplicate nodes）。
二叉查找树的C++实现
1. 节点和二叉查找树的定义
1.1 二叉查找树节点
template <class T>
class BSTNode{
public:
T key; // 关键字(键值)
BSTNode *left; // 左孩子
BSTNode *right; // 右孩子
BSTNode *parent;// 父结点 BSTNode(T value, BSTNode *p, BSTNode *l, BSTNode *r):
key(value),parent(),left(l),right(r) {}
};
BSTNode是二叉查找树的节点，它包含二叉查找树的几个基本信息：
(01) key -- 它是关键字，是用来对二叉查找树的节点进行排序的。
(02) left -- 它指向当前节点的左孩子。
(03) right -- 它指向当前节点的右孩子。
(04) parent -- 它指向当前节点的父结点。
1.2 二叉树操作
template <class T>
class BSTree {
private:
BSTNode<T> *mRoot; // 根结点 public:
BSTree();
~BSTree(); // 前序遍历"二叉树"
void preOrder();
// 中序遍历"二叉树"
void inOrder();
// 后序遍历"二叉树"
void postOrder(); // (递归实现)查找"二叉树"中键值为key的节点
BSTNode<T>* search(T key);
// (非递归实现)查找"二叉树"中键值为key的节点
BSTNode<T>* iterativeSearch(T key); // 查找最小结点：返回最小结点的键值。
T minimum();
// 查找最大结点：返回最大结点的键值。
T maximum(); // 找结点(x)的后继结点。即，查找"二叉树中数据值大于该结点"的"最小结点"。
BSTNode<T>* successor(BSTNode<T> *x);
// 找结点(x)的前驱结点。即，查找"二叉树中数据值小于该结点"的"最大结点"。
BSTNode<T>* predecessor(BSTNode<T> *x); // 将结点(key为节点键值)插入到二叉树中
void insert(T key); // 删除结点(key为节点键值)
void remove(T key); // 销毁二叉树
void destroy(); // 打印二叉树
void print();
private:
// 前序遍历"二叉树"
void preOrder(BSTNode<T>* tree) const;
// 中序遍历"二叉树"
void inOrder(BSTNode<T>* tree) const;
// 后序遍历"二叉树"
void postOrder(BSTNode<T>* tree) const; // (递归实现)查找"二叉树x"中键值为key的节点
BSTNode<T>* search(BSTNode<T>* x, T key) const;
// (非递归实现)查找"二叉树x"中键值为key的节点
BSTNode<T>* iterativeSearch(BSTNode<T>* x, T key) const; // 查找最小结点：返回tree为根结点的二叉树的最小结点。
BSTNode<T>* minimum(BSTNode<T>* tree);
// 查找最大结点：返回tree为根结点的二叉树的最大结点。
BSTNode<T>* maximum(BSTNode<T>* tree); // 将结点(z)插入到二叉树(tree)中
void insert(BSTNode<T>* &tree, BSTNode<T>* z); // 删除二叉树(tree)中的结点(z)，并返回被删除的结点
BSTNode<T>* remove(BSTNode<T>* &tree, BSTNode<T> *z); // 销毁二叉树
void destroy(BSTNode<T>* &tree); // 打印二叉树
void print(BSTNode<T>* tree, T key, int direction);
};
BSTree是二叉树。它包含二叉查找树的根节点和二叉查找树的操作。二叉查找树的操作中有许多重载函数，例如insert()函数，其中一个是内部接口，另一个是提供给外部的接口。
2 遍历
这里讲解前序遍历、中序遍历、后序遍历3种方式。
2.1 前序遍历
若二叉树非空，则执行以下操作：
(01) 访问根结点；
(02) 先序遍历左子树；
(03) 先序遍历右子树。
前序遍历代码
template <class T>
void BSTree<T>::preOrder(BSTNode<T>* tree) const
{
if(tree != NULL)
{
cout<< tree->key << " " ;
preOrder(tree->left);
preOrder(tree->right);
}
} template <class T>
void BSTree<T>::preOrder()
{
preOrder(mRoot);
}
2.2 中序遍历
若二叉树非空，则执行以下操作：
(01) 中序遍历左子树；
(02) 访问根结点；
(03) 中序遍历右子树。
中序遍历代码
template <class T>
void BSTree<T>::inOrder(BSTNode<T>* tree) const
{
if(tree != NULL)
{
inOrder(tree->left);
cout<< tree->key << " " ;
inOrder(tree->right);
}
} template <class T>
void BSTree<T>::inOrder()
{
inOrder(mRoot);
}
2.3 后序遍历
若二叉树非空，则执行以下操作：
(01) 后序遍历左子树；
(02) 后序遍历右子树；
(03) 访问根结点。
后序遍历代码
template <class T>
void BSTree<T>::postOrder(BSTNode<T>* tree) const
{
if(tree != NULL)
{
postOrder(tree->left);
postOrder(tree->right);
cout<< tree->key << " " ;
}
} template <class T>
void BSTree<T>::postOrder()
{
postOrder(mRoot);
}
看看下面这颗树的各种遍历方式：
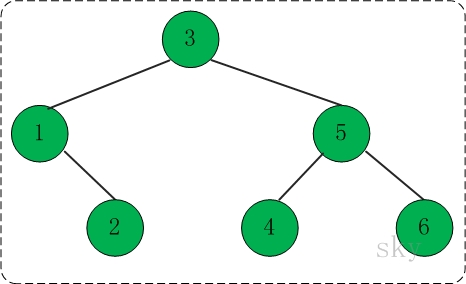
对于上面的二叉树而言，
(01) 前序遍历结果： 3 1 2 5 4 6
(02) 中序遍历结果： 1 2 3 4 5 6
(03) 后序遍历结果： 2 1 4 6 5 3
3. 查找
递归版本的代码
template <class T>
BSTNode<T>* BSTree<T>::search(BSTNode<T>* x, T key) const
{
if (x==NULL || x->key==key)
return x; if (key < x->key)
return search(x->left, key);
else
return search(x->right, key);
} template <class T>
BSTNode<T>* BSTree<T>::search(T key)
{
search(mRoot, key);
}
非递归版本的代码
template <class T>
BSTNode<T>* BSTree<T>::iterativeSearch(BSTNode<T>* x, T key) const
{
while ((x!=NULL) && (x->key!=key))
{
if (key < x->key)
x = x->left;
else
x = x->right;
} return x;
} template <class T>
BSTNode<T>* BSTree<T>::iterativeSearch(T key)
{
iterativeSearch(mRoot, key);
}
4. 最大值和最小值
查找最大值的代码
template <class T>
BSTNode<T>* BSTree<T>::maximum(BSTNode<T>* tree)
{
if (tree == NULL)
return NULL; while(tree->right != NULL)
tree = tree->right;
return tree;
} template <class T>
T BSTree<T>::maximum()
{
BSTNode<T> *p = maximum(mRoot);
if (p != NULL)
return p->key; return (T)NULL;
}
查找最小值的代码
template <class T>
BSTNode<T>* BSTree<T>::minimum(BSTNode<T>* tree)
{
if (tree == NULL)
return NULL; while(tree->left != NULL)
tree = tree->left;
return tree;
} template <class T>
T BSTree<T>::minimum()
{
BSTNode<T> *p = minimum(mRoot);
if (p != NULL)
return p->key; return (T)NULL;
}
5. 前驱和后继
节点的前驱：是该节点的左子树中的最大节点。
节点的后继：是该节点的右子树中的最小节点。
查找前驱节点的代码
/*
* 找结点(x)的前驱结点。即，查找"二叉树中数据值小于该结点"的"最大结点"。
*/
template <class T>
BSTNode<T>* BSTree<T>::predecessor(BSTNode<T> *x)
{
// 如果x存在左孩子，则"x的前驱结点"为 "以其左孩子为根的子树的最大结点"。
if (x->left != NULL)
return maximum(x->left); // 如果x没有左孩子。则x有以下两种可能：
// (01) x是"一个右孩子"，则"x的前驱结点"为 "它的父结点"。
// (01) x是"一个左孩子"，则查找"x的最低的父结点，并且该父结点要具有右孩子"，找到的这个"最低的父结点"就是"x的前驱结点"。
BSTNode<T>* y = x->parent;
while ((y!=NULL) && (x==y->left))
{
x = y;
y = y->parent;
} return y;
}
查找后继节点的代码
/*
* 找结点(x)的后继结点。即，查找"二叉树中数据值大于该结点"的"最小结点"。
*/
template <class T>
BSTNode<T>* BSTree<T>::successor(BSTNode<T> *x)
{
// 如果x存在右孩子，则"x的后继结点"为 "以其右孩子为根的子树的最小结点"。
if (x->right != NULL)
return minimum(x->right); // 如果x没有右孩子。则x有以下两种可能：
// (01) x是"一个左孩子"，则"x的后继结点"为 "它的父结点"。
// (02) x是"一个右孩子"，则查找"x的最低的父结点，并且该父结点要具有左孩子"，找到的这个"最低的父结点"就是"x的后继结点"。
BSTNode<T>* y = x->parent;
while ((y!=NULL) && (x==y->right))
{
x = y;
y = y->parent;
} return y;
}
6. 插入
插入节点的代码
/*
* 将结点插入到二叉树中
*
* 参数说明：
* tree 二叉树的根结点
* z 插入的结点
*/
template <class T>
void BSTree<T>::insert(BSTNode<T>* &tree, BSTNode<T>* z)
{
BSTNode<T> *y = NULL;
BSTNode<T> *x = tree; // 查找z的插入位置
while (x != NULL)
{
y = x;
if (z->key < x->key)
x = x->left;
else
x = x->right;
} z->parent = y;
if (y==NULL)
tree = z;
else if (z->key < y->key)
y->left = z;
else
y->right = z;
} /*
* 将结点(key为节点键值)插入到二叉树中
*
* 参数说明：
* tree 二叉树的根结点
* key 插入结点的键值
*/
template <class T>
void BSTree<T>::insert(T key)
{
BSTNode<T> *z=NULL; // 如果新建结点失败，则返回。
if ((z=new BSTNode<T>(key,NULL,NULL,NULL)) == NULL)
return ; insert(mRoot, z);
}
注：本文实现的二叉查找树是允许插入相同键值的节点的。若想禁止二叉查找树中插入相同键值的节点，可以参考"二叉查找树(一)之 图文解析 和 C语言的实现"中的插入函数进行修改。
7. 删除
删除节点的代码
/*
* 删除结点(z)，并返回被删除的结点
*
* 参数说明：
* tree 二叉树的根结点
* z 删除的结点
*/
template <class T>
BSTNode<T>* BSTree<T>::remove(BSTNode<T>* &tree, BSTNode<T> *z)
{
BSTNode<T> *x=NULL;
BSTNode<T> *y=NULL; if ((z->left == NULL) || (z->right == NULL) )
y = z;
else
y = successor(z); if (y->left != NULL)
x = y->left;
else
x = y->right; if (x != NULL)
x->parent = y->parent; if (y->parent == NULL)
tree = x;
else if (y == y->parent->left)
y->parent->left = x;
else
y->parent->right = x; if (y != z)
z->key = y->key; return y;
} /*
* 删除结点(z)，并返回被删除的结点
*
* 参数说明：
* tree 二叉树的根结点
* z 删除的结点
*/
template <class T>
void BSTree<T>::remove(T key)
{
BSTNode<T> *z, *node; if ((z = search(mRoot, key)) != NULL)
if ( (node = remove(mRoot, z)) != NULL)
delete node;
}
8. 打印
打印二叉查找树的代码
/*
* 打印"二叉查找树"
*
* key -- 节点的键值
* direction -- 0，表示该节点是根节点;
* -1，表示该节点是它的父结点的左孩子;
* 1，表示该节点是它的父结点的右孩子。
*/
template <class T>
void BSTree<T>::print(BSTNode<T>* tree, T key, int direction)
{
if(tree != NULL)
{
if(direction==) // tree是根节点
cout << setw() << tree->key << " is root" << endl;
else // tree是分支节点
cout << setw() << tree->key << " is " << setw() << key << "'s " << setw() << (direction==?"right child" : "left child") << endl; print(tree->left, tree->key, -);
print(tree->right,tree->key, );
}
} template <class T>
void BSTree<T>::print()
{
if (mRoot != NULL)
print(mRoot, mRoot->key, );
}
9. 销毁
销毁二叉查找树的代码
/*
* 销毁二叉树
*/
template <class T>
void BSTree<T>::destroy(BSTNode<T>* &tree)
{
if (tree==NULL)
return ; if (tree->left != NULL)
return destroy(tree->left);
if (tree->right != NULL)
return destroy(tree->right); delete tree;
tree=NULL;
} template <class T>
void BSTree<T>::destroy()
{
destroy(mRoot);
}
二叉查找树的C++实现(完整源码)
二叉查找树的C++实现文件(BSTree.h)
/**
* C++ 语言: 二叉查找树
*
* @author skywang
* @date 2013/11/07
*/ #ifndef _BINARY_SEARCH_TREE_HPP_
#define _BINARY_SEARCH_TREE_HPP_ #include <iomanip>
#include <iostream>
using namespace std; template <class T>
class BSTNode{
public:
T key; // 关键字(键值)
BSTNode *left; // 左孩子
BSTNode *right; // 右孩子
BSTNode *parent;// 父结点 BSTNode(T value, BSTNode *p, BSTNode *l, BSTNode *r):
key(value),parent(),left(l),right(r) {}
}; template <class T>
class BSTree {
private:
BSTNode<T> *mRoot; // 根结点 public:
BSTree();
~BSTree(); // 前序遍历"二叉树"
void preOrder();
// 中序遍历"二叉树"
void inOrder();
// 后序遍历"二叉树"
void postOrder(); // (递归实现)查找"二叉树"中键值为key的节点
BSTNode<T>* search(T key);
// (非递归实现)查找"二叉树"中键值为key的节点
BSTNode<T>* iterativeSearch(T key); // 查找最小结点：返回最小结点的键值。
T minimum();
// 查找最大结点：返回最大结点的键值。
T maximum(); // 找结点(x)的后继结点。即，查找"二叉树中数据值大于该结点"的"最小结点"。
BSTNode<T>* successor(BSTNode<T> *x);
// 找结点(x)的前驱结点。即，查找"二叉树中数据值小于该结点"的"最大结点"。
BSTNode<T>* predecessor(BSTNode<T> *x); // 将结点(key为节点键值)插入到二叉树中
void insert(T key); // 删除结点(key为节点键值)
void remove(T key); // 销毁二叉树
void destroy(); // 打印二叉树
void print();
private:
// 前序遍历"二叉树"
void preOrder(BSTNode<T>* tree) const;
// 中序遍历"二叉树"
void inOrder(BSTNode<T>* tree) const;
// 后序遍历"二叉树"
void postOrder(BSTNode<T>* tree) const; // (递归实现)查找"二叉树x"中键值为key的节点
BSTNode<T>* search(BSTNode<T>* x, T key) const;
// (非递归实现)查找"二叉树x"中键值为key的节点
BSTNode<T>* iterativeSearch(BSTNode<T>* x, T key) const; // 查找最小结点：返回tree为根结点的二叉树的最小结点。
BSTNode<T>* minimum(BSTNode<T>* tree);
// 查找最大结点：返回tree为根结点的二叉树的最大结点。
BSTNode<T>* maximum(BSTNode<T>* tree); // 将结点(z)插入到二叉树(tree)中
void insert(BSTNode<T>* &tree, BSTNode<T>* z); // 删除二叉树(tree)中的结点(z)，并返回被删除的结点
BSTNode<T>* remove(BSTNode<T>* &tree, BSTNode<T> *z); // 销毁二叉树
void destroy(BSTNode<T>* &tree); // 打印二叉树
void print(BSTNode<T>* tree, T key, int direction);
}; /*
* 构造函数
*/
template <class T>
BSTree<T>::BSTree():mRoot(NULL)
{
} /*
* 析构函数
*/
template <class T>
BSTree<T>::~BSTree()
{
destroy();
} /*
* 前序遍历"二叉树"
*/
template <class T>
void BSTree<T>::preOrder(BSTNode<T>* tree) const
{
if(tree != NULL)
{
cout<< tree->key << " " ;
preOrder(tree->left);
preOrder(tree->right);
}
} template <class T>
void BSTree<T>::preOrder()
{
preOrder(mRoot);
} /*
* 中序遍历"二叉树"
*/
template <class T>
void BSTree<T>::inOrder(BSTNode<T>* tree) const
{
if(tree != NULL)
{
inOrder(tree->left);
cout<< tree->key << " " ;
inOrder(tree->right);
}
} template <class T>
void BSTree<T>::inOrder()
{
inOrder(mRoot);
} /*
* 后序遍历"二叉树"
*/
template <class T>
void BSTree<T>::postOrder(BSTNode<T>* tree) const
{
if(tree != NULL)
{
postOrder(tree->left);
postOrder(tree->right);
cout<< tree->key << " " ;
}
} template <class T>
void BSTree<T>::postOrder()
{
postOrder(mRoot);
} /*
* (递归实现)查找"二叉树x"中键值为key的节点
*/
template <class T>
BSTNode<T>* BSTree<T>::search(BSTNode<T>* x, T key) const
{
if (x==NULL || x->key==key)
return x; if (key < x->key)
return search(x->left, key);
else
return search(x->right, key);
} template <class T>
BSTNode<T>* BSTree<T>::search(T key)
{
search(mRoot, key);
} /*
* (非递归实现)查找"二叉树x"中键值为key的节点
*/
template <class T>
BSTNode<T>* BSTree<T>::iterativeSearch(BSTNode<T>* x, T key) const
{
while ((x!=NULL) && (x->key!=key))
{
if (key < x->key)
x = x->left;
else
x = x->right;
} return x;
} template <class T>
BSTNode<T>* BSTree<T>::iterativeSearch(T key)
{
iterativeSearch(mRoot, key);
} /*
* 查找最小结点：返回tree为根结点的二叉树的最小结点。
*/
template <class T>
BSTNode<T>* BSTree<T>::minimum(BSTNode<T>* tree)
{
if (tree == NULL)
return NULL; while(tree->left != NULL)
tree = tree->left;
return tree;
} template <class T>
T BSTree<T>::minimum()
{
BSTNode<T> *p = minimum(mRoot);
if (p != NULL)
return p->key; return (T)NULL;
} /*
* 查找最大结点：返回tree为根结点的二叉树的最大结点。
*/
template <class T>
BSTNode<T>* BSTree<T>::maximum(BSTNode<T>* tree)
{
if (tree == NULL)
return NULL; while(tree->right != NULL)
tree = tree->right;
return tree;
} template <class T>
T BSTree<T>::maximum()
{
BSTNode<T> *p = maximum(mRoot);
if (p != NULL)
return p->key; return (T)NULL;
} /*
* 找结点(x)的后继结点。即，查找"二叉树中数据值大于该结点"的"最小结点"。
*/
template <class T>
BSTNode<T>* BSTree<T>::successor(BSTNode<T> *x)
{
// 如果x存在右孩子，则"x的后继结点"为 "以其右孩子为根的子树的最小结点"。
if (x->right != NULL)
return minimum(x->right); // 如果x没有右孩子。则x有以下两种可能：
// (01) x是"一个左孩子"，则"x的后继结点"为 "它的父结点"。
// (02) x是"一个右孩子"，则查找"x的最低的父结点，并且该父结点要具有左孩子"，找到的这个"最低的父结点"就是"x的后继结点"。
BSTNode<T>* y = x->parent;
while ((y!=NULL) && (x==y->right))
{
x = y;
y = y->parent;
} return y;
} /*
* 找结点(x)的前驱结点。即，查找"二叉树中数据值小于该结点"的"最大结点"。
*/
template <class T>
BSTNode<T>* BSTree<T>::predecessor(BSTNode<T> *x)
{
// 如果x存在左孩子，则"x的前驱结点"为 "以其左孩子为根的子树的最大结点"。
if (x->left != NULL)
return maximum(x->left); // 如果x没有左孩子。则x有以下两种可能：
// (01) x是"一个右孩子"，则"x的前驱结点"为 "它的父结点"。
// (01) x是"一个左孩子"，则查找"x的最低的父结点，并且该父结点要具有右孩子"，找到的这个"最低的父结点"就是"x的前驱结点"。
BSTNode<T>* y = x->parent;
while ((y!=NULL) && (x==y->left))
{
x = y;
y = y->parent;
} return y;
} /*
* 将结点插入到二叉树中
*
* 参数说明：
* tree 二叉树的根结点
* z 插入的结点
*/
template <class T>
void BSTree<T>::insert(BSTNode<T>* &tree, BSTNode<T>* z)
{
BSTNode<T> *y = NULL;
BSTNode<T> *x = tree; // 查找z的插入位置
while (x != NULL)
{
y = x;
if (z->key < x->key)
x = x->left;
else
x = x->right;
} z->parent = y;
if (y==NULL)
tree = z;
else if (z->key < y->key)
y->left = z;
else
y->right = z;
} /*
* 将结点(key为节点键值)插入到二叉树中
*
* 参数说明：
* tree 二叉树的根结点
* key 插入结点的键值
*/
template <class T>
void BSTree<T>::insert(T key)
{
BSTNode<T> *z=NULL; // 如果新建结点失败，则返回。
if ((z=new BSTNode<T>(key,NULL,NULL,NULL)) == NULL)
return ; insert(mRoot, z);
} /*
* 删除结点(z)，并返回被删除的结点
*
* 参数说明：
* tree 二叉树的根结点
* z 删除的结点
*/
template <class T>
BSTNode<T>* BSTree<T>::remove(BSTNode<T>* &tree, BSTNode<T> *z)
{
BSTNode<T> *x=NULL;
BSTNode<T> *y=NULL; if ((z->left == NULL) || (z->right == NULL) )
y = z;
else
y = successor(z); if (y->left != NULL)
x = y->left;
else
x = y->right; if (x != NULL)
x->parent = y->parent; if (y->parent == NULL)
tree = x;
else if (y == y->parent->left)
y->parent->left = x;
else
y->parent->right = x; if (y != z)
z->key = y->key; return y;
} /*
* 删除结点(z)，并返回被删除的结点
*
* 参数说明：
* tree 二叉树的根结点
* z 删除的结点
*/
template <class T>
void BSTree<T>::remove(T key)
{
BSTNode<T> *z, *node; if ((z = search(mRoot, key)) != NULL)
if ( (node = remove(mRoot, z)) != NULL)
delete node;
} /*
* 销毁二叉树
*/
template <class T>
void BSTree<T>::destroy(BSTNode<T>* &tree)
{
if (tree==NULL)
return ; if (tree->left != NULL)
return destroy(tree->left);
if (tree->right != NULL)
return destroy(tree->right); delete tree;
tree=NULL;
} template <class T>
void BSTree<T>::destroy()
{
destroy(mRoot);
} /*
* 打印"二叉查找树"
*
* key -- 节点的键值
* direction -- 0，表示该节点是根节点;
* -1，表示该节点是它的父结点的左孩子;
* 1，表示该节点是它的父结点的右孩子。
*/
template <class T>
void BSTree<T>::print(BSTNode<T>* tree, T key, int direction)
{
if(tree != NULL)
{
if(direction==) // tree是根节点
cout << setw() << tree->key << " is root" << endl;
else // tree是分支节点
cout << setw() << tree->key << " is " << setw() << key << "'s " << setw() << (direction==?"right child" : "left child") << endl; print(tree->left, tree->key, -);
print(tree->right,tree->key, );
}
} template <class T>
void BSTree<T>::print()
{
if (mRoot != NULL)
print(mRoot, mRoot->key, );
} #endif
二叉查找树的C++测试程序(BSTreeTest.cpp)
/**
* C++ 语言: 二叉查找树
*
* @author skywang
* @date 2013/11/07
*/ #include <iostream>
#include "BSTree.h"
using namespace std; static int arr[]= {,,,,,};
#define TBL_SIZE(a) ( (sizeof(a)) / (sizeof(a[0])) ) int main()
{
int i, ilen;
BSTree<int>* tree=new BSTree<int>(); cout << "== 依次添加: ";
ilen = TBL_SIZE(arr);
for(i=; i<ilen; i++)
{
cout << arr[i] <<" ";
tree->insert(arr[i]);
} cout << "\n== 前序遍历: ";
tree->preOrder(); cout << "\n== 中序遍历: ";
tree->inOrder(); cout << "\n== 后序遍历: ";
tree->postOrder();
cout << endl; cout << "== 最小值: " << tree->minimum() << endl;
cout << "== 最大值: " << tree->maximum() << endl;
cout << "== 树的详细信息: " << endl;
tree->print(); cout << "\n== 删除根节点: " << arr[];
tree->remove(arr[]); cout << "\n== 中序遍历: ";
tree->inOrder();
cout << endl; // 销毁二叉树
tree->destroy(); return ;
}
关于二叉查找树的C++实现有两点需要补充说明的:
第1点：采用了STL模板。因此，二叉查找树支持任意数据类型。
第2点：将二叉查找树的"声明"和"实现"都位于BSTree.h中。这是因为，在二叉查找树的实现采用了模板；而C++编译器不支持对模板的分离式编译！
二叉查找树的C++测试程序
上面的BSTreeTest.c是二叉查找树树的测试程序，运行结果如下：
== 依次添加:
== 前序遍历:
== 中序遍历:
== 后序遍历:
== 最小值:
== 最大值:
== 树的详细信息:
is root
is 's right child
is 's left child
is 's left child
is 's left child
is 's right child == 删除根节点:
== 中序遍历:
下面对测试程序的流程进行分析！
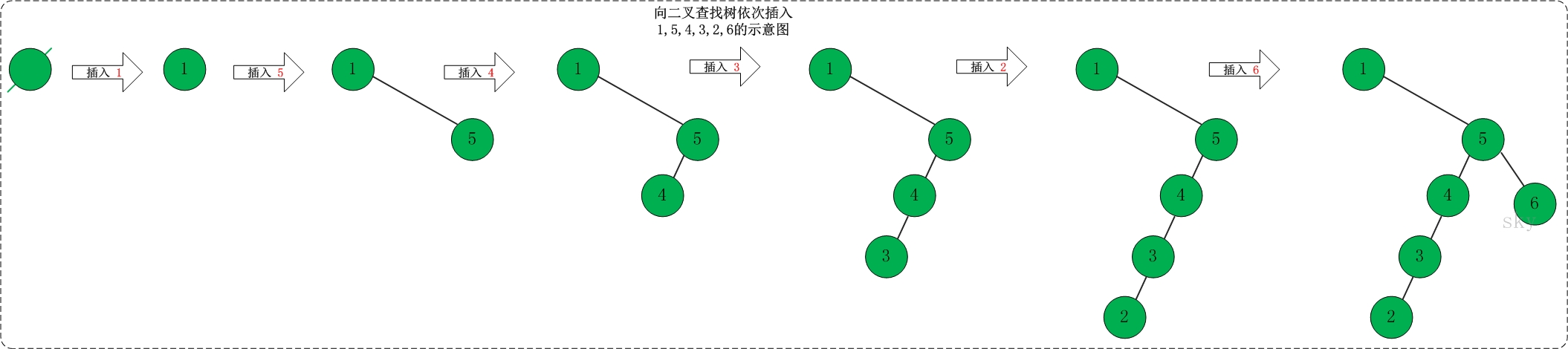
(01) 新建"二叉查找树"root。
(02) 向二叉查找树中依次插入1,5,4,3,2,6 。如下图所示：
(03) 遍历和查找
插入1,5,4,3,2,6之后，得到的二叉查找树如下：
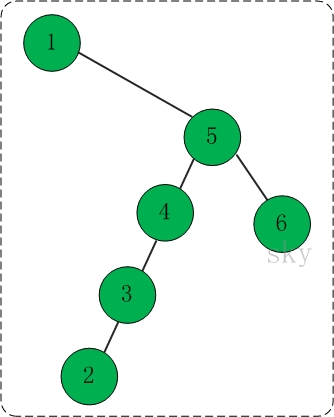
前序遍历结果: 1 5 4 3 2 6
中序遍历结果: 1 2 3 4 5 6
后序遍历结果: 2 3 4 6 5 1
最小值是1，而最大值是6。
(04) 删除节点4。如下图所示：
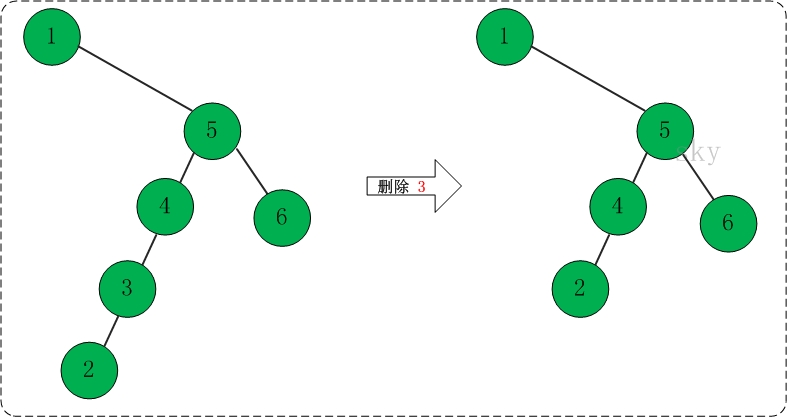
(05) 重新遍历该二叉查找树。
中序遍历结果: 1 2 4 5 6
二叉查找树(二)之 C++的实现的更多相关文章
- 二叉查找树(一)之 图文解析 和 C语言的实现
概要 本章先对二叉树的相关理论知识进行介绍,然后给出C语言的详细实现.关于二叉树的学习,需要说明的是:它并不难,不仅不难,而且它非常简单.初次接触树的时候,我也觉得它似乎很难:而之所产生这种感觉主要是 ...
- 二叉查找树(三)之 Java的实现
概要 在前面分别介绍了"二叉查找树的相关理论知识,然后给出了二叉查找树的C和C++实现版本".这一章写一写二叉查找树的Java实现版本. 目录 1. 二叉树查找树2. 二叉查找树的 ...
- C++数据结构之二叉查找树（BST）
C++数据结构之二叉查找树(BST) 二分查找法在算法家族大类中属于“分治法”,二分查找的过程比较简单,代码见我的另一篇日志,戳这里!因二分查找所涉及的有序表是一个向量,若有插入和删除结点的操作,则维 ...
- "《算法导论》之‘树’"：二叉查找树
树的介绍部分摘取自博文二叉查找树(一).二叉查找树(二).二叉查找树. 1. 树的介绍 1.1 树的定义 树是一种数据结构,它是由n(n>=1)个有限节点组成一个具有层次关系的集合. 把它叫做“ ...
- 【algo&ds】【吐血整理】4.树和二叉树、完全二叉树、满二叉树、二叉查找树、平衡二叉树、堆、哈夫曼树、B树、字典树、红黑树、跳表、散列表
本博客内容耗时4天整理,如果需要转载,请注明出处,谢谢. 1.树 1.1树的定义 在计算机科学中,树(英语:tree)是一种抽象数据类型(ADT)或是实作这种抽象数据类型的数据结构,用来模拟具有树状结 ...
- 数据结构中的树(二叉树、二叉搜索树、AVL树)
数据结构动图展示网站 树的概念 树(英语:tree)是一种抽象数据类型(ADT)或是实作这种抽象数据类型的数据结构,用来模拟具有树状结构性质的数据集合.它是由n(n>=1)个有限节点组成一个具有 ...
- Java实现二叉搜索树
原创:转载需注明原创地址 https://www.cnblogs.com/fanerwei222/p/11406176.html 尝试一下用Java实现二叉搜索树/二叉查找树,记录自己的学习历程. 1 ...
- 平衡二叉树（AVL Tree）
在学习算法的过程中,二叉平衡树是一定会碰到的,这篇博文尽可能简明易懂的介绍下二叉树的相关概念,然后着重讲下什么事平衡二叉树. (由于作图的时候忽略了箭头的问题,正常的树一般没有箭头,虽然不影响描述的过 ...
- mysql高级教程(一)-----逻辑架构、查询流程、索引
mysql逻辑架构 和其它数据库相比,MySQL有点与众不同,它的架构可以在多种不同场景中应用并发挥良好作用.主要体现在存储引擎的架构上,插件式的存储引擎架构将查询处理和其它的系统任务以及数据的存储提 ...
随机推荐
- 解决用navicate远程连接数据库出现1045 access denied for user 'root'@'localhost' using password yes
在mysql命令行中执行 SET PASSWORD FOR 'root'@'localhost' = PASSWORD('123456'); GRANT ALL PRIVILEGES ON *.* ...
- Mybatis多参传递的四种解决方案
Mybatis多参传递的四种解决方案 代码异常:org.apache.ibatis.binding.BindingException: Parameter 'param' not found. 长时间 ...
- Java并发包中Lock的实现原理
1. Lock 的简介及使用 Lock是java 1.5中引入的线程同步工具,它主要用于多线程下共享资源的控制.本质上Lock仅仅是一个接口(位于源码包中的java\util\concurrent\l ...
- Python：如何显示进度条
首先,推荐一个组件:progressive 效果如下: 进度条和一般的print区别在哪里呢? 答案就是print会输出一个\n,也就是换行符,这样光标移动到了下一行行首,接着输出,之前已经通过std ...
- 史上最强大的js图表库——ECharts带你入门(转)
出处:http://www.cnblogs.com/zrtqsk/p/4019412.html PS:之前的那篇博客Highcharts——让你的网页上图表画的飞起 ,评论中,花儿笑弯了腰 和 Sta ...
- XsdGen：通过自定义Attribute与反射自动生成XSD
前言 系统之间的数据交互往往需要事先定义一些契约,在WCF中我们需要先编写XSD文件,然后通过自动代码生成工具自动生成C#对象.对于刚刚接触契约的人来说,掌握XMLSpy之类的软件之后确实比手写XML ...
- XML 文档和数据
.NET Framework 4.5 其他版本 .NET Framework 提供了一组全面而集成的类,可用来方便地生成可以识别 XML 的应用程序. 通过以下命名空间中的类,可以分析和编写 XML, ...
- 原创教程：SpagoBI4.2汉化及配置Mysql数据库教程
SpagoBI4.2汉化及配置Mysql数据库教程 商务智能套件SpagoBI提供一个基于J2EE的框架用于管理BI对象如报表.OLAP分析.仪表盘.记分卡以及数据挖掘模型等的开源BI产品.它提供的B ...
- c#如何区分静态只读变量和常量
常量const 常量就是一个其值永远不会改变的静态字段.常量的值会在编译时自动推算,编译器会在遇到常量时,将其逐个替换为该常量的值.常量可以是C#内建的任何数字类型或枚举类型.声明一个常量的时候必须对 ...
- android 监听软键盘的收起与打开
参考: http://toughcoder.net/blog/2015/10/09/android-trick-detect-soft-keyboard-show-slash-hide/ packag ...