卡特兰数（catalan）总结

卡特兰数的公式

递推公式1：$f(n)=\sum \limits_{i=0}^{n-1}f(i)*f(n-i-1)$

递推公式2：$f(n)=\frac{f(n-1)*(4*n-2)}{n+1}$

组合公式1：$f(n)=\frac{C_{2n}^{n}}{n+1}$

组合公式2：$f(n)=C_{2n}^{n}-C_{2n}^{n-1}$

关于卡特兰数的题目

1. 有限制的网格方案数   eg网格

利用组合数的思想：

对于长N宽M的网格（下图2），方案数为 $C_{n+m}^{m}-C_{n+m}^{m-1}$

理解：走到（n，m）这个点总共要走n+m步，其中有m步一定是向上的，所以$C_{n+m}^{m}$这是所有情况

　　　但有不合法的情况，且不合法的一定经过绿线，将原图形沿其翻折，相当于走到c点，此时总n+m步不变，但只有m-1步是向右的

　　　所以$C_{n+m}^{m-1}$是不合法的

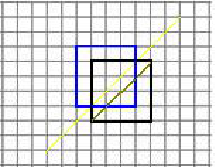
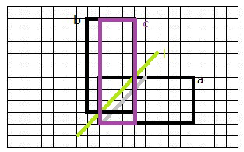                                                              （借用kaola学长的图）

对于N×N的网格就是卡特兰数了，如图一

本题先将式子化简，然后将其分解质因数，消去除法，最后乘上每个质数的个数次方就好

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<cmath>
 using namespace std;
 int n,m,num,p[],v[];
 int sum[];
 void prime(int x)
 {
     for(int i=;i<=x;i++)
     {
         if(!v[i])    {v[i]=i;p[++num]=i;}
         for(int j=;j<=num;j++){
             if(p[j]>v[i]||i*p[j]>x) continue;
             v[i*p[j]]=p[j];
         }
     }
 }
 int len=,ans[];
 void mul(int x)
 {
     int k=;
     for(int i=;i<=len;i++)
     {
         ans[i]=ans[i]*x+k;
         k=ans[i]/;
         ans[i]%=;
         if(k>&&i==len)  len++;
     }
 }
 int main()
 {
     ans[]=;
     scanf("%d%d",&n,&m);
     prime(n+m+);
     int t=n+-m;
     while(t>)
     {
         sum[v[t]]++;
         t/=v[t];
     }
     for(int i=n+m;i>=n+;i--)
     {
         t=i;
         while(t>)
         {
             sum[v[t]]++;
             t/=v[t];
         }
     }
     for(int i=;i<=m;i++)
     {
         t=i;
         while(t>)
         {
             sum[v[t]]--;
             t/=v[t];
         }
     }
     for(int i=;i<=num;i++)
         for(int j=;j<=sum[p[i]];j++)
             mul(p[i]);
     for(int i=len;i>=;i--)
         printf("%d",ans[i]);
     puts("");
 }

2.有趣的数列

其实这个也可以理解为上一个网格，将偶数位记为向右走一步，奇数位记为向上走一步，，偶数位之和大于奇数位之和，就是不能越过绿线

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<cmath>
 #define ll  long long
 using namespace std;
 const int maxn=;
 int n,mod,num;
 ll p[maxn];int v[maxn];
 ll sum[maxn];
 void prime(int x)
 {
     for(int i=;i<=x;i++)
     {
         if(!v[i])    {v[i]=i;p[++num]=i;}
         for(int j=;j<=num;j++){
             if(p[j]>v[i]||i*p[j]>x) break;
             v[i*p[j]]=p[j];
         }
     }
 }
 ll qpow(int a,int b)
 {
     ll ans=;
     while(b)
     {
         if(b&)  ans=ans*a%mod;
         a=a*a%mod;
         b>>=;
     }
     return ans%mod;
 }
 int  main()
 {
     scanf("%d%d",&n,&mod);
     prime(*n+);
     for(int i=*n;i>=n+;i--)
     {
         int t=i;
         while(t>)
         {
             sum[v[t]]++;
             t/=v[t];
         }
     }
     for(int i=;i<=n;i++)
     {
         int t=i;
         while(t>)
         {
             sum[v[t]]--;
             t/=v[t];
         }
     }
     ll ans=;
     for(int i=;i<=num;i++)
         if(sum[p[i]])
             ans=ans*qpow(p[i],sum[p[i]])%mod;
     printf("%lld\n",ans);
 }

3.树屋阶梯

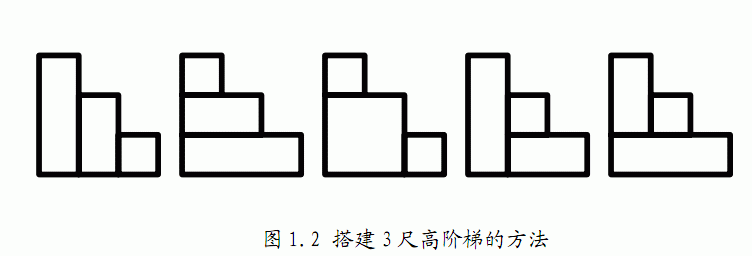
我们不妨手模样例，若扣去左下角直角所在矩形，

图一和图四的方案数为右面的2块的方案数×上面的0块的方案数，即为$f(3)+=f(2)*f(0)$

同理图二和图五为$f(3)+=f(0)*f(2)$   图三为$f(3)+=f(1)*f(1)$

由此可得  $f(n)=\sum \limits_{i=0}^{n-1}f(i)*f(n-i-1)$  卡特兰数公式1

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<cmath>
 using namespace std;
 int n,num,p[],v[];
 int sum[];
 void prime(int x)
 {
     for(int i=;i<=x;i++)
     {
         if(!v[i])    {v[i]=i;p[++num]=i;}
         for(int j=;j<=num;j++){
             if(p[j]>v[i]||i*p[j]>x) break;
             v[i*p[j]]=p[j];
         }
     }
 }
 int len=,ans[];
 void mul(int x)
 {
     int k=;
     for(int i=;i<=len;i++)
     {
         ans[i]=ans[i]*x+k;
         k=ans[i]/;
         ans[i]%=;
         if(k>&&i==len)  len++;
     }
 }
 int main()
 {
     ans[]=;
     scanf("%d",&n);
     prime(*n+);
     for(int i=*n;i>=n+;i--)
     {
         int t=i;
         while(t>)
         {
             sum[v[t]]++;
             t/=v[t];
         }
     }
     for(int i=;i<=n;i++)
     {
         int t=i;
         while(t>)
         {
             sum[v[t]]--;
             t/=v[t];
         }
     }
     for(int i=;i<=num;i++)
         for(int j=;j<=sum[p[i]];j++)
             mul(p[i]);
     for(int i=len;i>=;i--)
         printf("%d",ans[i]);
     puts("");
 }

关于卡特兰数的其他应用

1.出栈入栈问题：1，2，～n个数经过一个栈，合法的出栈序列$Cat(n)$

　　（引用学长的课件）出栈次序是卡特兰数的一个应用。 我们将入栈视为+1，出栈视为-1，则限制条件为在任意位置前缀和不小于0 。 我们讨论这个问题与卡特兰数有什么关系。 为了方便，我们按入栈的先后顺序将各个元素由1到n编号。 假设最后一个出栈的数为k。 则在k入栈之前，比k小的数一定全部出栈，所以这部分方案数为h(k-1)。 在k入栈之后，比k大的数在k入栈之后入栈，在k出栈之前出栈，所以这部分的方案数为h(n-k)。 这两部分互不干扰，则方案数为h(k-1)*h(n-k) 枚举k，得到的公式就是卡特兰数的递推公式。

2.左括号与右括号的匹配问题：n个左括号和n个右括号组成的合法括号序列$Cat(n)$

　　跟入栈出栈的理解是一样的

3.n个节点构成的二叉树的方案数为$Cat(n)$

　　假设左子树有$i$个节点，右子树有$n-i-1$个节点，i从0到n-1，根据乘法原理

可得公式1$f(n)=\sum \limits_{i=0}^{n-1}f(i)*f(n-i-1)$