[kuangbin带你飞]专题九 连通图B - Network UVA - 315

判断割点的性质：

如果点y满足

low[y]>=dfn[x] 且不是根节点

或者是根节点，满足上述式子的有两个及其以上。

就是割点

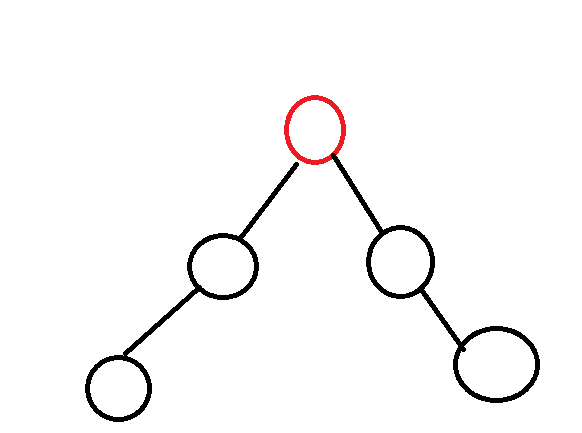
如果是起点，那么至少需要两个子节点满足上述条件，因为它是根节点，那么必须有至少两个节点的以及其儿子节点的时间戳是比这个值小的，如图，否则根节点也只是

一个叶子节点。

#include<iostream>
#include<string.h>
#include<algorithm>
#include<stdio.h>
using namespace std;
const int SIZE = ;
int head[SIZE],ver[SIZE*],Next[SIZE*];
int dfn[SIZE],low[SIZE],stack[SIZE];
bool cut[SIZE];
int n,m,tot,num,root;
void add(int x,int y)
{
    ver[++tot]=y,Next[tot]=head[x],head[x]=tot;
}
void tarjan(int x)
{
    dfn[x]=low[x]=++num;
    /*
      编号
    */
    int flag=;
    for (int i=head[x]; i; i=Next[i])
    {   /*
        遍历
        */
        int y=ver[i];
        if (!dfn[y])
        {
            tarjan(y);
            low[x]=min(low[x],low[y]);
            if (low[y]>=dfn[x]) /*割点的性质*/
            {
                //就是找到一个点，这个点的时间戳是比期所有子节点的最小时间戳都要小于或者等于的
                //那么我们只能通过这个点访问这个点
                flag++;
                if(x!=root || flag>)cut[x]=true;
                //如果是根节点，那么它要是割点前提是它必须要有两个以上的子节点满足上述条件
            }
        }
        else
        {
            low[x]=min(low[x],dfn[y]);
        }
    }
}
void init(){
    memset(low,,sizeof(low));
    memset(dfn,,sizeof(dfn));
    memset(Next,,sizeof(Next));
    memset(ver,,sizeof(ver));
    memset(head,,sizeof(head));
    memset(stack,,sizeof(stack));
    memset(cut,,sizeof(cut));
    tot=;
    num=;
}
int main()
{
    char s[];
    int a,b;
    char ch;
    while(scanf("%d",&n)&&n)
    {
        init();
        while(scanf("%d",&a)&&a)
        {
            while(scanf("%d%c",&b,&ch))
            {
                add(a,b);
                add(b,a);
                if (ch=='\n')break;
            }
        }
        int ans=;
        for (int i=; i<=n; i++)
        {
            if (!dfn[i])root=i,tarjan(i);
        }
        ans=;
        for (int i=; i<=n; i++)
        {
            if (cut[i])
            {
                ans++;
            }
        }
        printf("%d\n",ans);
    }
    return ;
}