BUAAOO-Third-Summary

一、从DBC到JML

契约式设计（Design by Contract）是一种开发软件的新思路。不妨通过商业活动的中真实的Contract（契约）来理解这个例子：

供应商必须提供某种产品（这是供应商的义务），并且有权期望客户付费（这是供应商的权利）。
客户必须支付费用（这是客户的义务），并且有权得到产品（这是客户的权利）。
双方必须满足应用于合约的某些义务，如法律和规定。

那我们可以从程序设计的角度看需要哪些契约呢：

可接受和不可接受的输入的值或类型，以及它们的含义
返回的值或类型，以及它们的含义
错误和异常的值或类型，以及它们的含义
副作用
先验条件
后验条件
不变性
（不太常见）性能保证，例如所需的时间和空间。我在后文中建立了性能相关的规格约定模式。

可以说JML是为DBC而生的（或者在学术上称之为DBC语言）。

我们从JML的原生语法来看，就非常符合契约设计的理念：

requires 描述先验条件
ensures 描述后验条件
old 描述和消除副作用
exceptional_behavior 描述错误和异常

所以说JML是教学和学术研究中对于DBC理论探索的一个利器。

形式化<->可以消除歧义。

形式化<->可以被程序读取！

形式化<->可以自动分析和推导！

这样，不仅写代码的人可以准确读懂需求，测试人员可以从测试上透视功能！

二、SMT solver 使用

笔者的java SMT代码一览，采用Microsoft Z3 SMT solver

    void prove(Context ctx, BoolExpr f, boolean useMBQI) throws TestFailedException

    {

        BoolExpr[] assumptions = new BoolExpr[0];

        prove(ctx, f, useMBQI, assumptions);

    }

    void prove(Context ctx, BoolExpr f, boolean useMBQI,

            BoolExpr... assumptions) throws TestFailedException

    {

        System.out.println("Proving: " + f);

        Solver s = ctx.mkSolver();

        Params p = ctx.mkParams();

        p.add("mbqi", useMBQI);

        s.setParameters(p);

        for (BoolExpr a : assumptions)

            s.add(a);

        s.add(ctx.mkNot(f));

        Status q = s.check();

        switch (q)

        {

        case UNKNOWN:

            System.out.println("Unknown because: " + s.getReasonUnknown());

            break;

        case SATISFIABLE:

            throw new TestFailedException();

        case UNSATISFIABLE:

            System.out.println("OK, proof: " + s.getProof());

            break;

        }

    }

    void disprove(Context ctx, BoolExpr f, boolean useMBQI)

        throws TestFailedException

    {

        BoolExpr[] a = {};

        disprove(ctx, f, useMBQI, a);

    }

    void disprove(Context ctx, BoolExpr f, boolean useMBQI,

            BoolExpr... assumptions) throws TestFailedException

    {

        System.out.println("Disproving: " + f);

        Solver s = ctx.mkSolver();

        Params p = ctx.mkParams();

        p.add("mbqi", useMBQI);

        s.setParameters(p);

        for (BoolExpr a : assumptions)

            s.add(a);

        s.add(ctx.mkNot(f));

        Status q = s.check();

        switch (q)

        {

        case UNKNOWN:

            System.out.println("Unknown because: " + s.getReasonUnknown());

            break;

        case SATISFIABLE:

            System.out.println("OK, model: " + s.getModel());

            break;

        case UNSATISFIABLE:

            throw new TestFailedException();

        }

    }

跑一个简单的数独验证先测试一下SMT 在本地有效（代码来自官方template，有很多改动）

    void sudokuExample(Context ctx) throws TestFailedException

    {

        System.out.println("SudokuExample");

        Log.append("SudokuExample");

        // 9x9 matrix of integer variables

        IntExpr[][] X = new IntExpr[9][];

        for (int i = 0; i < 9; i++)

        {

            X[i] = new IntExpr[9];

            for (int j = 0; j < 9; j++)

                X[i][j] = (IntExpr) ctx.mkConst(

                        ctx.mkSymbol("x_" + (i + 1) + "_" + (j + 1)),

                        ctx.getIntSort());

        }

        // each cell contains a value in {1, ..., 9}

        BoolExpr[][] cells_c = new BoolExpr[9][];

        for (int i = 0; i < 9; i++)

        {

            cells_c[i] = new BoolExpr[9];

            for (int j = 0; j < 9; j++)

                cells_c[i][j] = ctx.mkAnd(ctx.mkLe(ctx.mkInt(1), X[i][j]),

                        ctx.mkLe(X[i][j], ctx.mkInt(9)));

        }

        // each row contains a digit at most once

        BoolExpr[] rows_c = new BoolExpr[9];

        for (int i = 0; i < 9; i++)

            rows_c[i] = ctx.mkDistinct(X[i]);

        // each column contains a digit at most once

        BoolExpr[] cols_c = new BoolExpr[9];

        for (int j = 0; j < 9; j++)

            cols_c[j] = ctx.mkDistinct(X[j]);

        // each 3x3 square contains a digit at most once

        BoolExpr[][] sq_c = new BoolExpr[3][];

        for (int i0 = 0; i0 < 3; i0++)

        {

            sq_c[i0] = new BoolExpr[3];

            for (int j0 = 0; j0 < 3; j0++)

            {

                IntExpr[] square = new IntExpr[9];

                for (int i = 0; i < 3; i++)

                    for (int j = 0; j < 3; j++)

                        square[3 * i + j] = X[3 * i0 + i][3 * j0 + j];

                sq_c[i0][j0] = ctx.mkDistinct(square);

            }

        }

        BoolExpr sudoku_c = ctx.mkTrue();

        for (BoolExpr[] t : cells_c)

            sudoku_c = ctx.mkAnd(ctx.mkAnd(t), sudoku_c);

        sudoku_c = ctx.mkAnd(ctx.mkAnd(rows_c), sudoku_c);

        sudoku_c = ctx.mkAnd(ctx.mkAnd(cols_c), sudoku_c);

        for (BoolExpr[] t : sq_c)

            sudoku_c = ctx.mkAnd(ctx.mkAnd(t), sudoku_c);

        // sudoku instance, we use '0' for empty cells

        int[][] instance = { { 0, 0, 0, 0, 9, 4, 0, 3, 0 },

                { 0, 0, 0, 5, 1, 0, 0, 0, 7 }, { 0, 8, 9, 0, 0, 0, 0, 4, 0 },

                { 0, 0, 0, 0, 0, 0, 2, 0, 8 }, { 0, 6, 0, 2, 0, 1, 0, 5, 0 },

                { 1, 0, 2, 0, 0, 0, 0, 0, 0 }, { 0, 7, 0, 0, 0, 0, 5, 2, 0 },

                { 9, 0, 0, 0, 6, 5, 0, 0, 0 }, { 0, 4, 0, 9, 7, 0, 0, 0, 0 } };

        BoolExpr instance_c = ctx.mkTrue();

        for (int i = 0; i < 9; i++)

            for (int j = 0; j < 9; j++)

                instance_c = ctx.mkAnd(

                        instance_c,

                        (BoolExpr) ctx.mkITE(

                                ctx.mkEq(ctx.mkInt(instance[i][j]),

                                        ctx.mkInt(0)), ctx.mkTrue(),

                                ctx.mkEq(X[i][j], ctx.mkInt(instance[i][j]))));

        Solver s = ctx.mkSolver();

        s.add(sudoku_c);

        s.add(instance_c);

        if (s.check() == Status.SATISFIABLE)

        {

            Model m = s.getModel();

            Expr[][] R = new Expr[9][9];

            for (int i = 0; i < 9; i++)

                for (int j = 0; j < 9; j++)

                    R[i][j] = m.evaluate(X[i][j], false);

            System.out.println("Sudoku solution:");

            for (int i = 0; i < 9; i++)

            {

                for (int j = 0; j < 9; j++)

                    System.out.print(" " + R[i][j]);

                System.out.println();

            }

        } else

        {

            System.out.println("Failed to solve sudoku");

            throw new TestFailedException();

        }

    }

用SMT solver 很难测试像图论这样的问题，所以我的策略是先测试一个经典的数独问题，如上。

此外我做了两个测试：

验证连通块个数实验

这种验证确实非常高级非常有效，但是写代码还是相当长的，（包括生成代码和模板代码）。

测试用代码如下



	private BoolExpr generate(BinopExpr expr) {

		BoolExpr ret = null;

		if(expr instanceof ConditionExpr){

			//get two sides and the operator

			ConditionExpr condExpr = (ConditionExpr)expr;

			//lhs can either be constant or a local

			//12-29-14, not right now when we

			//have more general formula

			Value lhs = condExpr.getOp1();

			IntExpr lhsExpr = evaluateExpr(lhs);

			//rhs can also be an arithmetic expression

			//from converting assignments to equality

			Value rhs = condExpr.getOp2();

			ArithExpr rhsExpr = null;

			//add conditionals here first to check

			if(rhs instanceof BinopExpr){

				BinopExpr rhsBinop = (BinopExpr) rhs;

				IntExpr lhsArith = evaluateExpr(rhsBinop.getOp1());

				IntExpr rhsArith = evaluateExpr(rhsBinop.getOp2());

				//now determine the operator add, sub, mult

				try {

					if(rhsBinop instanceof AddExpr){

						ArithExpr[] operands = new ArithExpr[]{lhsArith, rhsArith};

						rhsExpr = ctx.MkAdd(operands);

					} else if (rhsBinop instanceof SubExpr){

						ArithExpr[] operands = new ArithExpr[]{lhsArith, rhsArith};

						rhsExpr = ctx.MkSub(operands);

					} else if (rhsBinop instanceof MulExpr){

						ArithExpr[] operands = new ArithExpr[]{lhsArith, rhsArith};

						rhsExpr = ctx.MkMul(operands);

					} else if (rhsBinop instanceof DivExpr){

						rhsExpr = ctx.MkDiv(lhsArith, rhsArith);

					} else if(rhsBinop instanceof RemExpr){

						rhsExpr = ctx.MkMod(lhsArith, rhsArith);

					} else if (rhsBinop instanceof ShrExpr){

						//can only handle when rhs,i.e., y is not a variable

						// x >> y = x / (2^y)

						if(rhsArith.IsArithmeticNumeral()){

							IntNum number = (IntNum)rhsArith;

							rhsArith = ctx.MkInt(1<<number.Int()); // this is 2^y

							rhsExpr = ctx.MkDiv(lhsArith, rhsArith);

						} else {

							System.out.println("Rhs in ShrExpr is not a number " + rhsArith.getClass());

							System.exit(2);

						}

					} else if(rhsBinop instanceof ShlExpr){

						//can only handle when rhs, i.e., u is not a variable

						// x << y = x * (2^y)

						if(rhsArith.IsArithmeticNumeral()){

							IntNum number = (IntNum)rhsArith;

							rhsArith = ctx.MkInt(1<<number.Int()); // this is 2^y

							ArithExpr[] operands = new ArithExpr[]{lhsArith, rhsArith};

							rhsExpr = ctx.MkMul(operands);

						} else {

							System.out.println("Rhs in ShlExpr is not a number " + rhsArith.getClass());

							System.exit(2);

						}

					} else {

						System.out.println("Cannot process rhsBinop " + rhsBinop.getClass());

						System.exit(2);

					}

				} catch (Z3Exception e) {

					e.printStackTrace();

				}

			} else if (rhs instanceof NegExpr){

				try {

					ArithExpr[] operands;

					operands = new ArithExpr[]{ctx.MkInt(0), evaluateExpr(((NegExpr)rhs).getOp())};

					rhsExpr = ctx.MkSub(operands);

				} catch (Z3Exception e) {

					e.printStackTrace();

				}

			} else  {

				rhsExpr = evaluateExpr(rhs);

			}

			//now generate the condition

			try {

				if(expr instanceof EqExpr){

					ret = ctx.MkEq(lhsExpr, rhsExpr);

				} else if (expr instanceof GeExpr){

					ret = ctx.MkGe(lhsExpr, rhsExpr);

				} else if (expr instanceof GtExpr){

					ret = ctx.MkGt(lhsExpr, rhsExpr);

				} else if (expr instanceof LeExpr){

					ret = ctx.MkLe(lhsExpr, rhsExpr);

				} else if (expr instanceof LtExpr){

					ret = ctx.MkLt(lhsExpr, rhsExpr);

				} else if (expr instanceof NeExpr){

					ret = ctx.MkNot(ctx.MkEq(lhsExpr, rhsExpr));

				}

			} catch (Z3Exception e) {

				e.printStackTrace();

			}

		} else if (expr instanceof OrExpr){

			BoolExpr lhs = generate((BinopExpr)expr.getOp1());

			BoolExpr rhs = generate((BinopExpr)expr.getOp2());

			try {

				ret = ctx.MkOr(new BoolExpr[]{lhs, rhs});

			} catch (Z3Exception e) {

				e.printStackTrace();

			}

		} else if (expr instanceof AndExpr){

			BoolExpr lhs = generate((BinopExpr)expr.getOp1());

			BoolExpr rhs = generate((BinopExpr)expr.getOp2());

			try {

				ret = ctx.MkAnd(new BoolExpr[]{lhs, rhs});

			} catch (Z3Exception e) {

				e.printStackTrace();

			}

		} else {

			//something else that we don't handle yet :(

			System.out.println("Cannot process " + expr);

			System.exit(2);

		}

		return ret;

	}

public boolean disjoint_solve(BoolExpr z3Formula){

	boolean ret = true;

	try {

		Solver solver = ctx.MkSolver();

		Params p = ctx.MkParams();

		p.Add("soft_timeout", timeout);

		solver.setParameters(p);

		solver.Assert(z3Formula);

		Status result = solver.Check();

		if(result.equals(Status.SATISFIABLE)){

			ret = true;

		} else if (result.equals(Status.UNSATISFIABLE)){

			ret = false;

		} else {

			//unknown

			System.out.println("Warning: " + result + " for " + z3Formula);

		}

	} catch (Z3Exception e) {

		// TODO Auto-generated catch block

		e.printStackTrace();

	}

	return ret;

}

验证多个最短路算法的等价性

此外，部分代码在python下（验证）^_

三、JML toolchain 用于测试

目前JML的工具有这些：

ESC/Java2 1, an extended static checker which uses JML annotations to perform more rigorous static checking than is otherwise possible.
OpenJML declares itself the successor of ESC/Java2.
Daikon, a dynamic invariant generator.
KeY, which provides an open source theorem prover with a JML front-end and an Eclipse plug-in (JML Editing) with support for syntax highlighting of JML.
Krakatoa, a static verification tool based on the Why verification platform and using the Coq proof assistant.
JMLEclipse, a plugin for the Eclipse integrated development environment with support for JML syntax and interfaces to various tools that make use of JML annotations.
Sireum/Kiasan, a symbolic execution based static analyzer which supports JML as a contract language.
JMLUnit, a tool to generate files for running JUnit tests on JML annotated Java files.
TACO, an open source program analysis tool that statically checks the compliance of a Java program against its Java Modeling Language specification.
VerCors verifier

但是这些工具并不能满足我的开发和证明要求，由于我后续加入，我自行开发了一个命令行工具 Advanced JML check with TesTNG ( AJCT )。（功能很不完善）。

其原理其实是OpenJML + JMLUnitNG + jprofiler + Python + Bash 的一个组合脚本。

根据我自己的类生成的测试代码截图如下：

生成结果如下

.

├── AJCT

├── Main.java

├── Mydisgraph.java

├── Mydisgraph_sssp_int_euler_path_gen.class

├── Mydisgraph_sssp_int_euler_path_gen.java

├── Mydisgraph_sssp_int_general_gen.class

├── Mydisgraph_sssp_int_general_gen.java

├── Mydisgraph_sssp_int_rebuild_gen.class

├── Mydisgraph_sssp_int_rebuild_gen.java

├── Mydisgraph_sssp_int_shortest_path_tree_gen.class

├── Mydisgraph_sssp_int_shortest_path_tree_gen.java

├── MyGraph_containsEdge_int_int.class

├── MyGraph_containsEdge_int_int.java

├── MyGraph_containsNode_int.class

├── MyGraph_containsNode_int.java

├── MyGraph_getnodelabel_int.class

├── MyGraph_getnodelabel_int.java

├── MyGraph_getShortestPathLength_int_int.class

├── MyGraph_getShortestPathLength_int_int.java

├── MyGraph_isConnected_int_int.class

├── MyGraph_isConnected_int_int.java

├── MyGraph.java

├── MyNode.java

├── MyPathContainer.java

├── MyPath.java

├── MyRailwaySystem_getFa_int.class

├── MyRailwaySystem_getFa_int.java

├── MyRailwaySystem_getLeastTicketPrice_int_int.class

├── MyRailwaySystem_getLeastTicketPrice_int_int.java

├── MyRailwaySystem_getLeastTransferCount_int_int.class

├── MyRailwaySystem_getLeastTransferCount_int_int.java

├── MyRailwaySystem_getLeastUnpleasantValue_int_int.class

├── MyRailwaySystem_getLeastUnpleasantValue_int_int.java

├── MyRailwaySystem.java

├── MyRailwaySystem_merge_int_int.class

└── MyRailwaySystem_merge_int_int.java

测试结果截图如下：

性能测试结果如下：

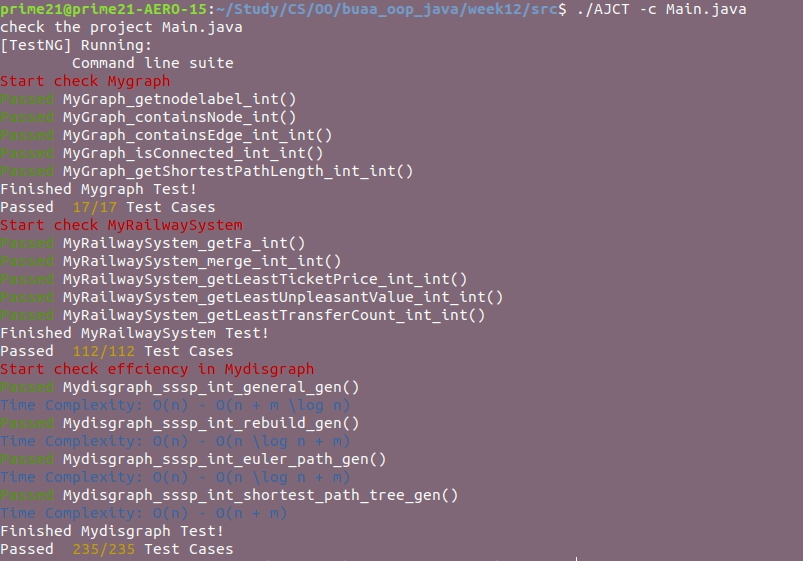
四、规格完善策略

我发现了现有的规格体系的一个缺点：即无法保证描述方法的时空间复杂度，因此，我在此基础上，加入了关于复杂度的描述规格，用于测试我自己的代码。

（目前，我的规格只能测试图的最短路算法和图论其他基本算法。）

我的复杂度规格描述策略如下：

pre-condition: 表示算法中某一些集合，和他们的大小范围。
parameter: 表示参数属于算法中的哪一个集合，和他们的大小范围。
time complexity: 用时间复杂度的标准形式，要求有 online, offline, worst-case几个关键描述。（省略大O记号）
space complexity: 用空间复杂度的标准形式。

这部分的开发过程有很多困难，由于还没有彻底完善，不方便开源（还在做进一步测试）。

引入这个规格的考虑有如下考量：

后续重构要考量该接口是否会丧失原有性能、导致各种问题（进程不同步、需求无法满足）。
对调用者友好，能不用透视代码，而从性能和功能两个层次考量是否调用该方法、调用的条件是什么。
对验证有效，工程问题的正确性和效率（开发效率、测试效率）都和基本的性能要求分不开，能提前做好性能的规格设计，在没有遇到性能问题之前大概率无需顾虑。
性能规格可以做理论推导、可以通过调用方法和后续方法的性能规格推导该规格的bound，做到防御性设计。

关于我的性能测试报告可以看我的优化博客，在此只做简要的叙述。

在性能测试阶段，利用多种输入情况对程序的运行时间情况做拟合，得到的表达式和规格表达式对比，从而得到验证复杂度的效果。

我的验证结果如下

利用

$f(n) - g(n)$ 这样的表达式表达：修改复杂度为$f(n)$，询问复杂度为$g(n)$

algo \ case	general gen	rebuild gen	Euler path gen	shortest path tree gen
A-star-algorithm	$O(n^2)-O(n+m)$	$O(n^2)-O(n+m)$	$O(n^2)-O(n+m)$	$O(n+m)-O(n+m)$
$O(n^2)$ transfer line algorithm	$O(n^2)-O(m)$	$O(n^2)-O(m)$	$O(n^2)-O(m)$	$O(n^2)-O(m)$
my algorithm	$O(n)-O(n + m \log n) $	$O(n)-O(n \log n + m) $	$O(n)-O(n \log n + m) $	$O(n)-O(n + m) $
floyd algorithm	$O(n^3)-O(1) $	$O(n^3)-O(1) $	$O(n^3)-O(1) $	$O(n^3)-O(1) $

五、架构设计

这次的架构设计有助教和老师的经验在里面，我们自己设计的部分不多！老师和助教的前瞻性充分在这个单元体现出来。

第一次的架构，非常基本

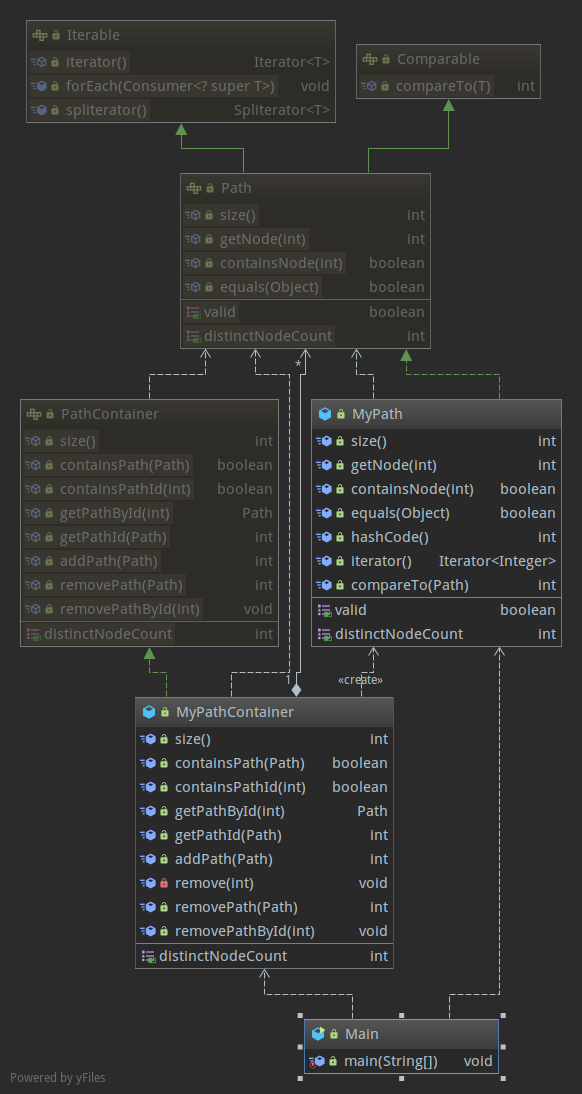
第二次的架构，非常基本

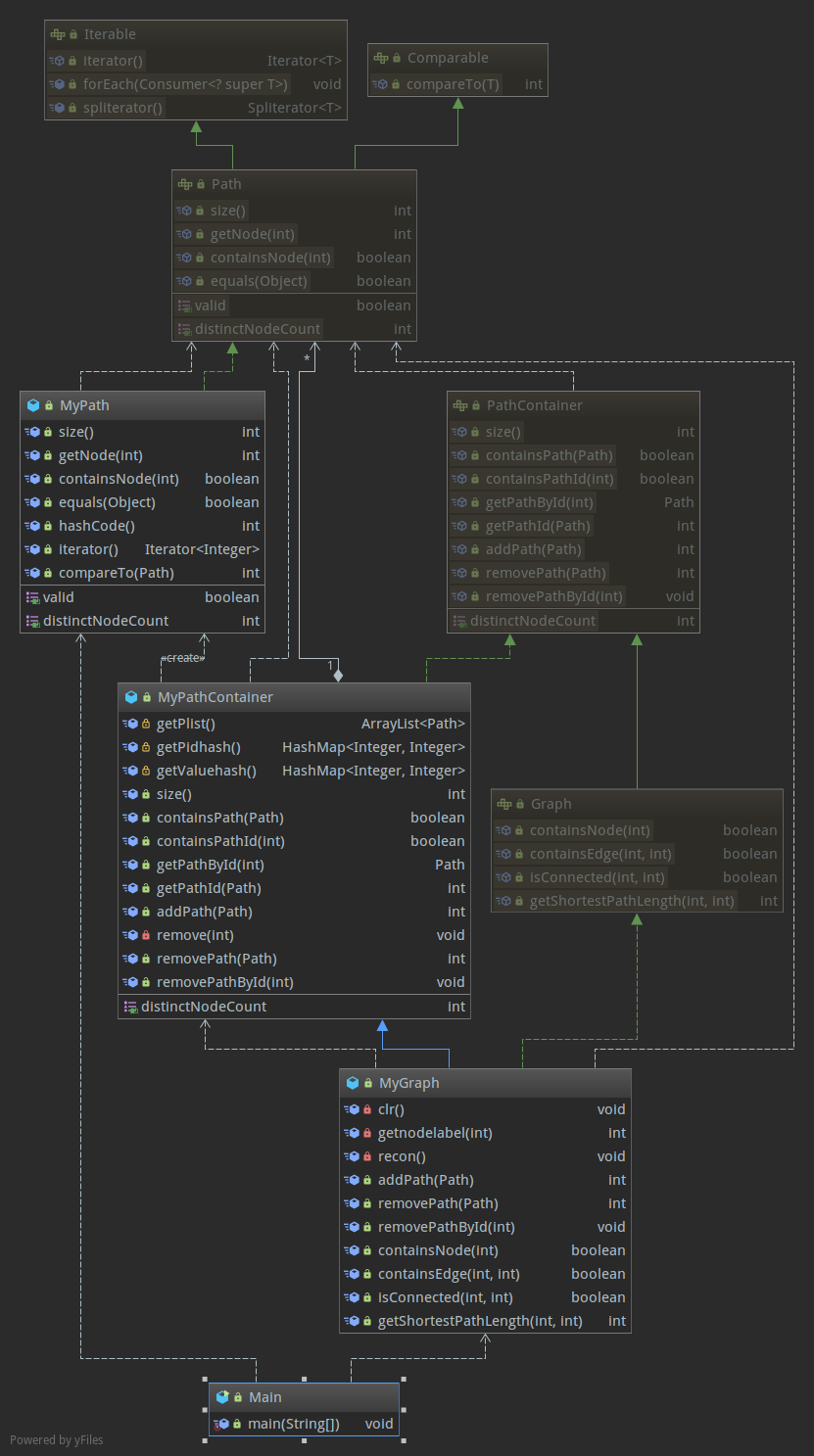
第三次，抽象出了Mydisgraph 封装出了最短路算法

用于：

随时调试性能
随时替换其他算法
封装共性代码

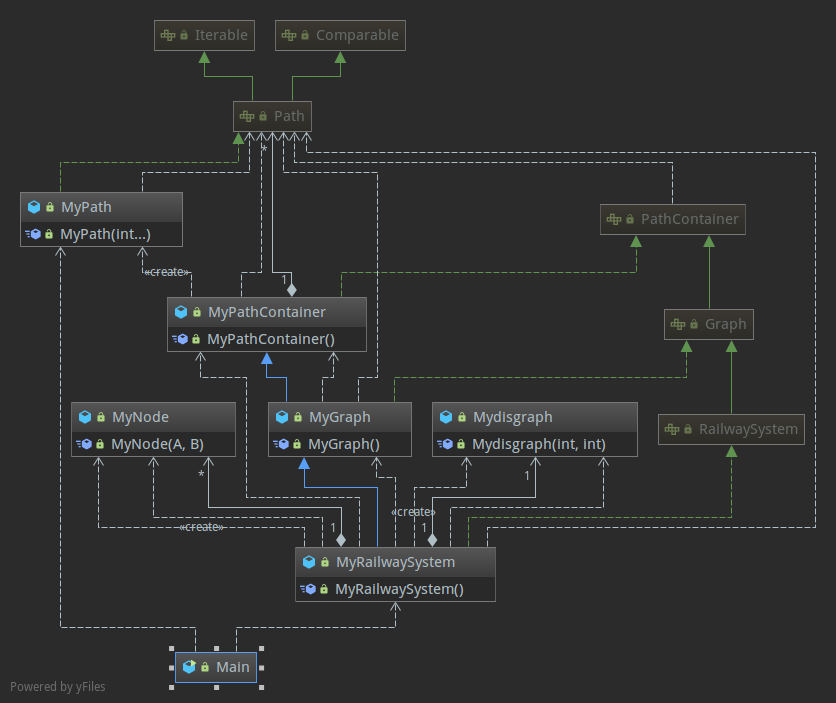
三次的架构一脉相成在架构上我改进了以前的开发策略：

学习相关的模式、接口设计、画流程图（确定如何对象的属性）
模块绑定、避免重构
做头脑风暴，考察多种测试数据和思路，并完成代码
测试数据构造和覆盖性测试
代码回顾和思考

由此我实现了代码的复用和解耦。

六、debug情况

我发现了一个核心bug，滥用hashcode

有同学的第一次代码在equals方法内直接用hashcode判断，我使用了中间相遇的思路攻击了他的hash算法：

示例如下：

PATH_ADD 1 1 1

PATH_ADD 1 29792

这两条路径具有相同的hashcode。

这里其实反映了要如何使用hashcode的问题，hashcode的冲突要用equals去避免，值得同学记忆。

七、心得体会

经过这一段时间对JML规格的阅读以及上次上机时自己真正尝试写JML规格，我深深感受到了JML语言的重要性。只有使用JML语言，在进行程序编写，特别是不同人组队完成一个大型程序的编写时，才可以在最大程度上保证不同人完成在代码可以融合在一起，而不会产生各种各样奇妙的bug。

在这一单元的学习后，对前置条件，后置条件，副作用，有了比较好的理解，这是一个方法行为的核心，有了这样的规范，程序员间可以在架构层面上进行交流，也就可以在编码前期，架构设计时期进行交流，减少实现时的错误。这是我在这一单元最为印象深刻的，之后使用JML，我会在代码的注释中写明前置条件，后置条件，以及副作用，保持一个良好的习惯。

感谢OO感谢OO课程教会了我从规格层次审视代码，从更高的角度去设计去思考，做代码的主人。