Embedding Layer

在深度学习实验中经常会遇Eembedding层,然而网络上的介绍可谓是相当含糊。比如 Keras中文文档中对嵌入层 Embedding的介绍除了一句 “嵌入层将正整数（下标）转换为具有固定大小的向量”之外就不愿做过多的解释。那么我们为什么要使用嵌入层 Embedding呢? 主要有这两大原因:

1、使用One-hot 方法编码的向量会很高维也很稀疏。假设我们在做自然语言处理（NLP）中遇到了一个包含2000个词的字典，当时用One-hot编码时，每一个词会被一个包含2000个整数的向量来表示，其中1999个数字是0，要是我的字典再大一点的话这种方法的计算效率岂不是大打折扣？

2、训练神经网络的过程中，每个嵌入的向量都会得到更新。如果你看到了博客上面的图片你就会发现在多维空间中词与词之间有多少相似性，这使我们能可视化的了解词语之间的关系，不仅仅是词语，任何能通过嵌入层 Embedding 转换成向量的内容都可以这样做。

Eg 1:

对于句子“deep learning is very deep”：

使用嵌入层embedding 的第一步是通过索引对该句子进行编码，这里我们给每一个不同的句子分配一个索引，上面的句子就会变成这样：

"1 2 3 4 1"

接下来会创建嵌入矩阵，我们要决定每一个索引需要分配多少个‘潜在因子’，这大体上意味着我们想要多长的向量，通常使用的情况是长度分配为32和50。在这篇博客中，为了保持文章可读性这里为每个索引指定6个潜在因子。这样，我们就可以使用嵌入矩阵来而不是庞大的one-hot编码向量来保持每个向量更小。简而言之，嵌入层embedding在这里做的就是把单词“deep”用向量[.32, .02, .48, .21, .56, .15]来表达。然而并不是每一个单词都会被一个向量来代替，而是被替换为用于查找嵌入矩阵中向量的索引。

eg 2:

假如我们有一个100W X10W的矩阵，用它乘上一个10W X 20的矩阵，我们可以把它降到100W X 20，瞬间量级降了。。。10W/20=5000倍！！！

这就是嵌入层的一个作用——降维。

然后中间那个10W X 20的矩阵，可以理解为查询表，也可以理解为映射表，也可以理解为过度表；

参考链接：https://blog.csdn.net/weixin_42078618/article/details/82999906

https://blog.csdn.net/u010412858/article/details/77848878

PS: pixel wise metric learning

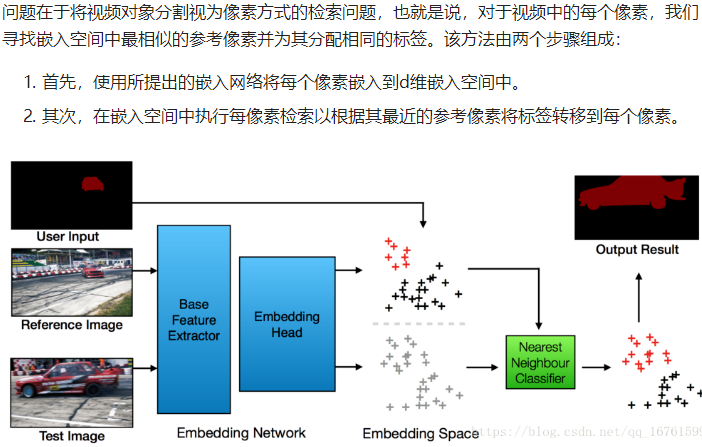
嵌入模型：在所提出的模型f中，其中每个像素x j,i被表示为d维嵌入向量ej,i = f(xj,i)。理想地，属于相同对象的像素在嵌入空间中彼此靠近，并且属于不同对象的像素彼此远离。