Technocup 2020 Elimination Round 3题解
\(A\)
曲明连sb模拟不会做，拖出去埋了算了
//quming
#include<bits/stdc++.h>
#define R register
#define fi first
#define se second
#define fp(i,a,b) for(R int i=(a),I=(b)+1;i<I;++i)
#define fd(i,a,b) for(R int i=(a),I=(b)-1;i>I;--i)
#define go(u) for(int i=head[u],v=e[i].v;i;i=e[i].nx,v=e[i].v)
template<class T>inline bool cmax(T&a,const T&b){return a<b?a=b,1:0;}
template<class T>inline bool cmin(T&a,const T&b){return a>b?a=b,1:0;}
using namespace std;
typedef pair<int,int> pi;
const int N=2005;
char s[N];int n,k,top,T;pi st[N];
void find(int pos,int c){
if(s[pos]==c)return;
fp(i,pos+1,n)if(s[i]==c){
st[++top]=pi(pos,i),reverse(s+pos,s+i+1);
return;
}
}
int main(){
for(scanf("%d",&T);T;--T){
scanf("%d%d",&n,&k),top=0,--k;
scanf("%s",s+1);
fp(i,1,k<<1)find(i,(i&1)?'(':')');
R int sz=n-(k<<1);
fp(i,1,sz)find(i+(k<<1),i<=sz?'(':')');
printf("%d\n",top);
fp(i,1,top)printf("%d %d\n",st[i].fi,st[i].se);
}
return 0;
}
\(B\)
离线之后sort一下依次加入每个元素，每次查询\(k\)大值就行了，我抄了个平衡树板子，实际上二分+树状数组就行了
//quming
#include<bits/stdc++.h>
#define R register
#define pb push_back
#define fp(i,a,b) for(R int i=(a),I=(b)+1;i<I;++i)
#define fd(i,a,b) for(R int i=(a),I=(b)-1;i>I;--i)
#define go(u) for(int i=head[u],v=e[i].v;i;i=e[i].nx,v=e[i].v)
template<class T>inline bool cmax(T&a,const T&b){return a<b?a=b,1:0;}
template<class T>inline bool cmin(T&a,const T&b){return a>b?a=b,1:0;}
using namespace std;
unsigned int aaa=19260817;
inline unsigned int rd(){aaa^=aaa>>15,aaa+=aaa<<12,aaa^=aaa>>3;return aaa;}
const int N=2e5+5;
struct node;typedef node* ptr;
struct node{
ptr lc,rc;int v,sz;unsigned int pr;
inline void init(R int val){v=val,pr=rd(),sz=1;}
inline ptr upd(){return sz=lc->sz+rc->sz+1,this;}
}e[N],*rt=e;int tot;
inline ptr newnode(R int v){return e[++tot].init(v),(e+tot)->lc=(e+tot)->rc=e,e+tot;}
void split(ptr p,int k,ptr &s,ptr &t){
if(p==e)return s=t=e,void();
if(p->v<=k)s=p,split(p->rc,k,p->rc,t);
else t=p,split(p->lc,k,s,p->lc);
p->upd();
}
ptr merge(ptr s,ptr t){
if(s==e)return t;if(t==e)return s;
if(s->pr<t->pr)return s->rc=merge(s->rc,t),s->upd();
return t->lc=merge(s,t->lc),t->upd();
}
void insert(int k){
ptr s,t;
split(rt,k,s,t);
rt=merge(merge(s,newnode(k)),t);
}
void erase(int k){
ptr s,t,p;
split(rt,k,s,t),split(s,k-1,s,p),p=merge(p->lc,p->rc);
rt=merge(merge(s,p),t);
}
int rk(int k){
ptr s,t;int now;
split(rt,k-1,s,t);now=s->sz+1;
return rt=merge(s,t),now;
}
int Kth(ptr p,int k){
if(p->lc->sz==k-1)return p->v;
if(p->lc->sz>=k)return Kth(p->lc,k);
return Kth(p->rc,k-p->lc->sz-1);
}
int Pre(int k){
ptr s,t;int now;
split(rt,k-1,s,t),now=Kth(s,s->sz);
return rt=merge(s,t),now;
}
int nxt(int k){
ptr s,t;int now;
split(rt,k,s,t),now=Kth(t,1);
return rt=merge(s,t),now;
}
int a[N],id[N],ak[N],ad[N],ans[N],n,m;
vector<int>qr[N];
int main(){
scanf("%d",&n);
fp(i,1,n)scanf("%d",&a[i]),id[i]=i;
sort(id+1,id+1+n,[](const int &x,const int &y){return a[x]==a[y]?x<y:a[x]>a[y];});
scanf("%d",&m);
fp(i,1,m)scanf("%d%d",&ak[i],&ad[i]),qr[ak[i]].pb(i);
fp(i,1,n){
insert(id[i]);
for(auto v:qr[i])ans[v]=Kth(rt,ad[v]);
}
fp(i,1,m)printf("%d\n",a[ans[i]]);
return 0;
}
\(C\)
曲明连sb二分都不会做，可以拖出去埋了
//quming
#include<bits/stdc++.h>
#define R register
#define fp(i,a,b) for(R int i=(a),I=(b)+1;i<I;++i)
#define fd(i,a,b) for(R int i=(a),I=(b)-1;i>I;--i)
#define go(u) for(int i=head[u],v=e[i].v;i;i=e[i].nx,v=e[i].v)
template<class T>inline bool cmax(T&a,const T&b){return a<b?a=b,1:0;}
template<class T>inline bool cmin(T&a,const T&b){return a>b?a=b,1:0;}
using namespace std;
const int N=1e6+5;
char s[N];
vector<int>sm[N],a[N],d[N],g[N];
int n,m,cnt,h,t,l,r,mid,ans;
inline void init(){
fp(i,0,n+1){
sm[i].resize(m+2),
a[i].resize(m+2),
d[i].resize(m+2),
g[i].resize(m+2);
}
}
inline int calc(R int x,R int y,R int xx,R int yy){
return sm[xx][yy]+sm[x-1][y-1]-sm[x-1][yy]-sm[xx][y-1];
}
inline bool ok(R int i,R int j,R int mid){
return calc(i-mid,j-mid,i+mid,j+mid)==(mid<<1|1)*(mid<<1|1);
}
bool ck(){
fp(i,0,n+1)fp(j,0,m+1)g[i][j]=0;
fp(i,mid+1,n-mid)fp(j,mid+1,m-mid)
if(ok(i,j,mid)){
++g[i-mid][j-mid],++g[i+mid+1][j+mid+1];
--g[i-mid][j+mid+1],--g[i+mid+1][j-mid];
}
R int fl=1;
fp(i,1,n)fp(j,1,m){
g[i][j]+=g[i-1][j]+g[i][j-1]-g[i-1][j-1];
if((g[i][j]>0)!=a[i][j])fl=0;
}
return fl;
}
int main(){
// freopen("testdata.in","r",stdin);
scanf("%d%d",&n,&m);init();
fp(i,1,n){
scanf("%s",s+1);
fp(j,1,m){
a[i][j]=(s[j]=='X');
sm[i][j]=sm[i-1][j]+sm[i][j-1]-sm[i-1][j-1]+a[i][j];
}
}
l=0,r=min(n+1,m+1)>>1,ans=0;
while(l<=r){
mid=(l+r)>>1;
ck()?(ans=mid,l=mid+1):r=mid-1;
}
printf("%d\n",ans);
fp(i,1,n)fp(j,1,m)d[i][j]=0;
fp(i,ans+1,n-ans)fp(j,ans+1,m-ans)d[i][j]=ok(i,j,ans);
fp(i,1,n){
fp(j,1,m)putchar(d[i][j]?'X':'.');
putchar('\n');
}
return 0;
}
\(D\)
记一个\(c\)，考虑每个\(i\)，如果\(a_i=h_i\)令\(--c\)，如果\(a_i=h_{i+1}\)令\(++c\)，相当于求最终\(c>0\)的方案，那么根据\(h_i\)和\(h_{i+1}\)是否相等判断一下\(a_i\)对\(c\)的贡献写出生成函数，手动多项式快速幂就行了
//quming
#include<bits/stdc++.h>
#define R register
#define fp(i,a,b) for(R int i=(a),I=(b)+1;i<I;++i)
#define fd(i,a,b) for(R int i=(a),I=(b)-1;i>I;--i)
#define go(u) for(int i=head[u],v=e[i].v;i;i=e[i].nx,v=e[i].v)
template<class T>inline bool cmax(T&a,const T&b){return a<b?a=b,1:0;}
template<class T>inline bool cmin(T&a,const T&b){return a>b?a=b,1:0;}
using namespace std;
const int P=998244353;
inline void upd(R int &x,R int y){(x+=y)>=P?x-=P:0;}
inline int inc(R int x,R int y){return x+y>=P?x+y-P:x+y;}
inline int dec(R int x,R int y){return x-y<0?x-y+P:x-y;}
inline int mul(R int x,R int y){return 1ll*x*y-1ll*x*y/P*P;}
int ksm(R int x,R int y){
R int res=1;
for(;y;y>>=1,x=mul(x,x))(y&1)?res=mul(res,x):0;
return res;
}
const int N=(1<<19)+5;
int rt[2][N],r[21][N],inv[21],lg[N],lim,d;
void init(){
fp(d,1,19){
fp(i,1,(1<<d)-1)r[d][i]=(r[d][i>>1]>>1)|((i&1)<<(d-1));
inv[d]=ksm(1<<d,P-2),lg[1<<d]=d;
}
for(R int t=(P-1)>>1,i=1,x,y;i<524288;t>>=1,i<<=1){
x=ksm(3,t),y=ksm(332748118,t),rt[0][i]=rt[1][i]=1;
fp(k,1,i-1){
rt[0][i+k]=mul(rt[0][i+k-1],x);
rt[1][i+k]=mul(rt[1][i+k-1],y);
}
}
}
void NTT(int *A,int ty){
int t;
fp(i,0,lim-1)if(i<r[d][i])swap(A[i],A[r[d][i]]);
for(R int mid=1;mid<lim;mid<<=1)
for(R int j=0;j<lim;j+=(mid<<1))
fp(k,0,mid-1){
A[j+k+mid]=inc(A[j+k],P-(t=mul(A[j+k+mid],rt[ty][mid+k])));
upd(A[j+k],t);
}
if(!ty){
t=inv[d];
fp(i,0,lim-1)A[i]=mul(A[i],t);
}
}
int A[N],a[N];
int n,k,res,coef,cnt;
int main(){
// freopen("testdata.in","r",stdin);
init();
scanf("%d%d",&n,&k);
fp(i,1,n)scanf("%d",&a[i]);
a[n+1]=a[1];
fp(i,1,n)++(a[i]==a[i+1]?coef:cnt);
if(coef==n)return puts("0"),0;
coef=ksm(k%P,coef);
A[0]=A[2]=1,A[1]=(k-2)%P;
lim=1,d=0;while(lim<=(cnt<<1))lim<<=1,++d;
NTT(A,1);
fp(i,0,lim-1)A[i]=ksm(A[i],cnt);
NTT(A,0);
fp(i,cnt+1,(cnt<<1))upd(res,A[i]);
printf("%d\n",mul(res,coef));
return 0;
}
\(E\)
首先默认\(a_i\leq a_{i+1}\)，并且默认\(a_i\leq n-1\)
这样的话我们就可以有一种放法，对于一个\(n\times n\)的网格，强制副对角线上所有格子不能放元素，然后每一列都从这一列的副对角线格子上方开始放起，这样由于\(a_i\leq a_{i+1}\)，所以相邻两列的放了元素的格子的顶端一定不同
大概长这样，红色表示不能放，黑色表示放了的格子，\(a_2=a_3=a_4=2\)，但它们的顶端各不相同
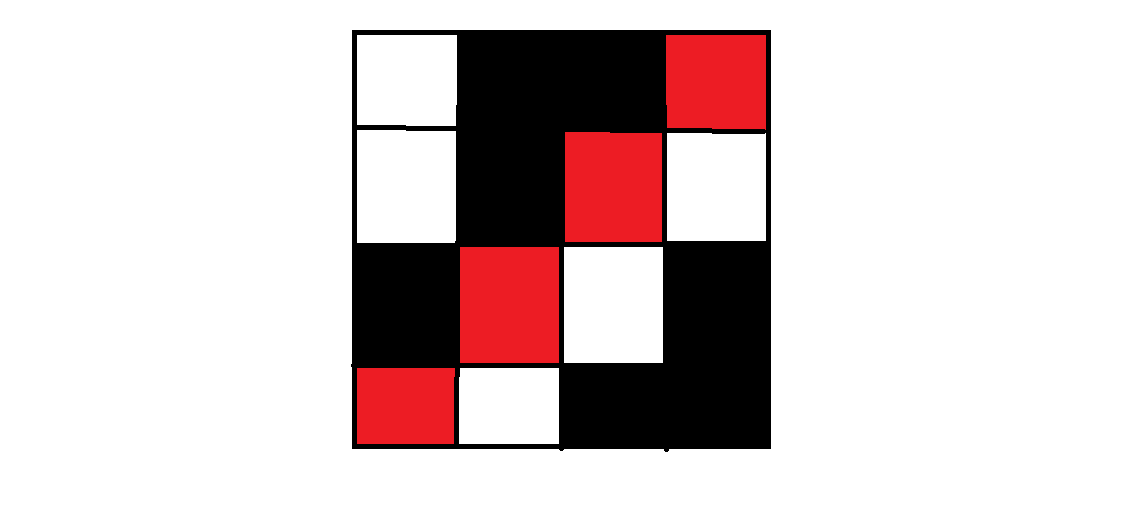
这样的话我们可以证明任意两行一定不同
如果有的元素满足\(a_i=n\)，然后我们直接把它的第\(n\)个元素扔到第\(n+1\)行，有可能出现的一个问题就是第\(n\)行和第\(n+1\)行相等。一种解决办法就是我们找到第\(n+1\)行的黑格子的左边界，记为\(i\)，由于\(i\)是左边界，那么第\(n\)行里第\(i-1\)个格子一定是白的，我们把第\(n+1\)行第\(i\)个格子和第\(i\)列副对角线上那个格子交换，容易证明这样之后依然是合法的
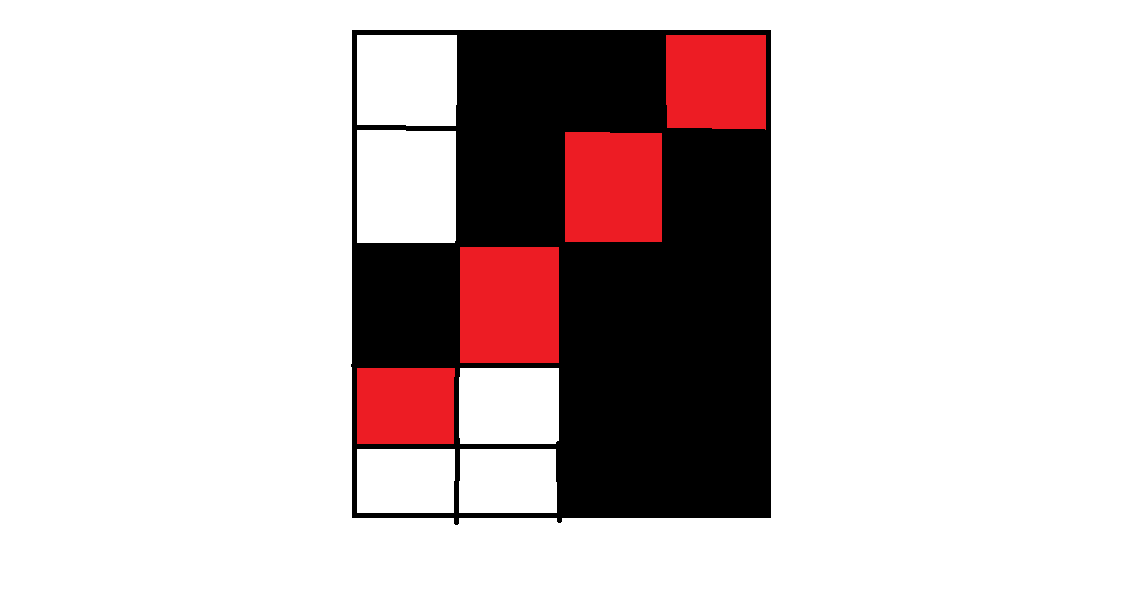
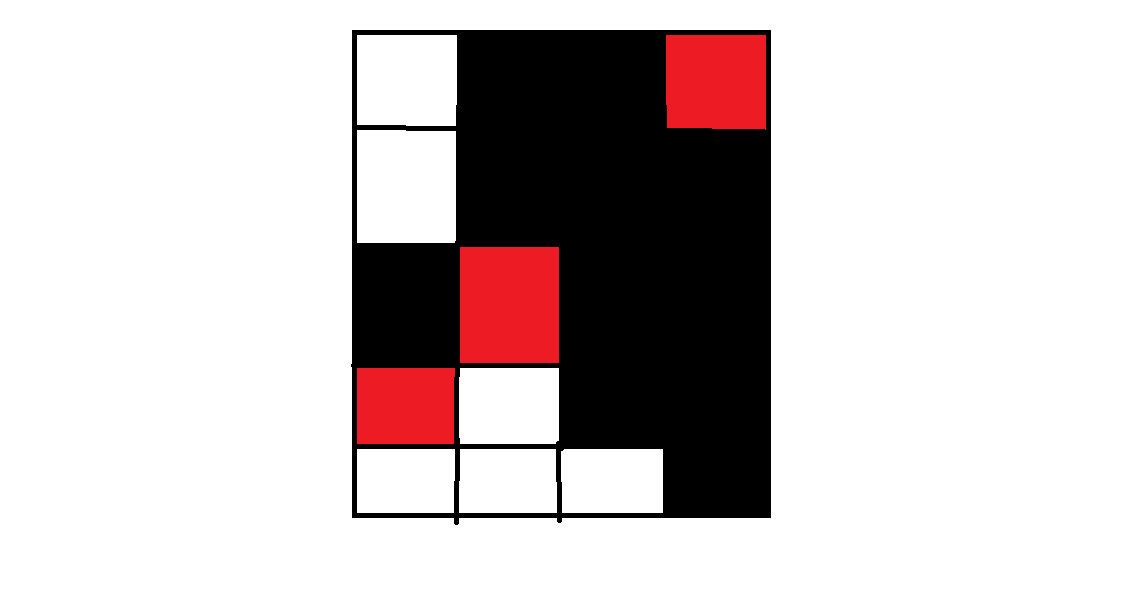
//quming
#include<bits/stdc++.h>
#define R register
#define fp(i,a,b) for(R int i=(a),I=(b)+1;i<I;++i)
#define fd(i,a,b) for(R int i=(a),I=(b)-1;i>I;--i)
#define go(u) for(int i=head[u],v=e[i].v;i;i=e[i].nx,v=e[i].v)
template<class T>inline bool cmax(T&a,const T&b){return a<b?a=b,1:0;}
template<class T>inline bool cmin(T&a,const T&b){return a>b?a=b,1:0;}
using namespace std;
const int N=1005;
int mp[N][N],a[N],id[N],n;
int main(){
// freopen("testdata.in","r",stdin);
scanf("%d",&n);
fp(i,1,n)scanf("%d",&a[i]),id[i]=i;
sort(id+1,id+1+n,[](const int &x,const int &y){return a[x]<a[y];});
fd(i,n,1)for(R int j=n-i,k=1;k<=min(n-1,a[id[i]]);++k,--j){
if(!j)j=n;
mp[j][id[i]]=1;
}
fp(i,1,n)if(a[i]==n)mp[n+1][i]=1;
R bool fl=1;
fp(i,1,n)if(mp[n][i]!=mp[n+1][i]){fl=0;break;}
if(fl){
// puts("QAQ");
fd(i,n,1)if(a[id[i]]==n&&a[id[i-1]]!=n){
mp[n+1][id[i]]=0,mp[n-i+1][id[i]]=1;
break;
}
}
printf("%d\n",n+1);
fp(i,1,n+1){
fp(j,1,n)putchar(mp[i][j]+'0');
putchar('\n');
}
return 0;
}
\(F\)
我们把所有的线段都拆成形如\([x,x+2^k-1]\)的样子，其中\(x\)的二进制的\(0\)到\(k-1\)位全都为\(0\)，对于一条原来的线段，拆掉它之后产生的所有线段其实就是\(l\)和\(r\)的trie树上的路径的所有儿子，所以我们可以证明拆完之后总线段数是\(O(n\times 60)\)的
对于两条形如\([x,x+2^k-1]\)和\([y,y+2^g-1]\)的线段，假设\(k<g\)，并设\(p=x\oplus y\)的前\(59-g\)位，我们发现这两条线段可以异或出\([p,p+2^g-1]\)之间的所有数字，而且\(p\)是一个固定的前缀。所以我们可以枚举所有合法的线段，而最终的贡献就相当于trie树的一个子树全部合法，打上标记就行了，最后在trie树上dfs一遍就行了，总复杂度\(O(n^260^3)\)，卡一卡就能过
//quming
#include<bits/stdc++.h>
#define R register
#define fi first
#define se second
#define fp(i,a,b) for(R int i=(a),I=(b)+1;i<I;++i)
#define fd(i,a,b) for(R int i=(a),I=(b)-1;i>I;--i)
#define go(u) for(int i=head[u],v=e[i].v;i;i=e[i].nx,v=e[i].v)
template<class T>inline bool cmax(T&a,const T&b){return a<b?a=b,1:0;}
template<class T>inline bool cmin(T&a,const T&b){return a>b?a=b,1:0;}
using namespace std;
const int P=998244353;
inline void upd(R int &x,R int y){(x+=y)>=P?x-=P:0;}
inline int inc(R int x,R int y){return x+y>=P?x+y-P:x+y;}
inline int dec(R int x,R int y){return x-y<0?x-y+P:x-y;}
inline int mul(R int x,R int y){return 1ll*x*y-1ll*x*y/P*P;}
int ksm(R int x,R int y){
R int res=1;
for(;y;y>>=1,x=mul(x,x))(y&1)?res=mul(res,x):0;
return res;
}
typedef long long ll;
typedef pair<ll,int> pi;
typedef pair<ll,ll> ppi;
const int N=200005;
int n,na,nb,top;pi sa[N],sb[N];ppi st[N];
void get(){
scanf("%d",&n);
fp(i,1,n)scanf("%lld%lld",&st[i].fi,&st[i].se);
sort(st+1,st+1+n,[](const ppi &a,const ppi &b){return a.fi<b.fi;});
top=1;
fp(i,2,n)if(st[i].fi<=st[top].se+1)cmax(st[top].se,st[i].se);
else st[++top]=st[i];
}
void build(pi *s,int &n,ll l,ll r){
for(R ll i=l,p=0;i<=r;i+=(1ll<<p)){
while((i>>p&1^1)&&(i+(1ll<<(p+1))-1)<=r)++p;
while(p&&(i+(1ll<<p)-1)>r)--p;
s[++n]=pi(i,p);
}
}
const int M=1e7+5;
int ch[M][2],vis[M],bin[233],nd,res;
void ins(R ll x,int k){
R int p=0,c;
fd(i,59,k){
c=(x>>i&1);
if(!ch[p][c])ch[p][c]=++nd;
if(vis[p=ch[p][c]])return;
}
vis[p]=1;
}
void dfs(int p,int pos,int coef){
if(vis[p]){
upd(res,mul(coef,bin[pos+1]));
upd(res,mul(bin[pos+1]-1,bin[pos]));
return;
}
if(ch[p][0])dfs(ch[p][0],pos-1,coef);
if(ch[p][1])dfs(ch[p][1],pos-1,inc(coef,bin[pos]));
}
int main(){
// freopen("testdata.in","r",stdin);
get();
fp(i,1,top)build(sa,na,st[i].fi,st[i].se);
get();
fp(i,1,top)build(sb,nb,st[i].fi,st[i].se);
bin[0]=1;fp(i,1,60)bin[i]=mul(bin[i-1],2);
sort(sa+1,sa+1+na,[](const pi &a,const pi &b){return a.se>b.se;});
sort(sb+1,sb+1+nb,[](const pi &a,const pi &b){return a.se>b.se;});
fp(i,1,na)fp(j,1,nb)ins(sa[i].fi^sb[j].fi,max(sa[i].se,sb[j].se));
dfs(0,59,0);
printf("%lld\n",res);
return 0;
}
Technocup 2020 Elimination Round 3题解的更多相关文章
- Codeforces Round #606 (Div. 2, based on Technocup 2020 Elimination Round 4) 题解
Happy Birthday, Polycarp! Make Them Odd As Simple as One and Two Let's Play the Words? Two Fairs Bea ...
- Codeforces Round #591 (Div. 2, based on Technocup 2020 Elimination Round 1) 题解
A..B略 C 对当前的值排序,再二分答案,然后对于(i%x==0 && i%y==0)放入大的,再放其他的贪心解决即可. #include<iostream> #incl ...
- Codeforces Round #596 (Div. 2, based on Technocup 2020 Elimination Round 2)
A - Forgetting Things 题意:给 \(a,b\) 两个数字的开头数字(1~9),求使得等式 \(a=b-1\) 成立的一组 \(a,b\) ,无解输出-1. 题解:很显然只有 \( ...
- 20191214 Codeforces Round #606 (Div. 2, based on Technocup 2020 Elimination Round 4)
概述 切了 ABCE,Room83 第一 还行吧 A - Happy Birthday, Polycarp! 题解 显然这样的数不会很多. 于是可以通过构造法,直接求出 \([1,10^9]\) 内所 ...
- Codeforces Round #602 (Div. 2, based on Technocup 2020 Elimination Round 3) F2. Wrong Answer on test 233 (Hard Version) dp 数学
F2. Wrong Answer on test 233 (Hard Version) Your program fails again. This time it gets "Wrong ...
- Codeforces Round #602 (Div. 2, based on Technocup 2020 Elimination Round 3) E. Arson In Berland Forest 二分 前缀和
E. Arson In Berland Forest The Berland Forest can be represented as an infinite cell plane. Every ce ...
- Codeforces Round #602 (Div. 2, based on Technocup 2020 Elimination Round 3) D2. Optimal Subsequences (Hard Version) 数据结构 贪心
D2. Optimal Subsequences (Hard Version) This is the harder version of the problem. In this version, ...
- Codeforces Round #602 (Div. 2, based on Technocup 2020 Elimination Round 3) C. Messy 构造
C. Messy You are fed up with your messy room, so you decided to clean it up. Your room is a bracket ...
- Codeforces Round #602 (Div. 2, based on Technocup 2020 Elimination Round 3) B. Box 贪心
B. Box Permutation p is a sequence of integers p=[p1,p2,-,pn], consisting of n distinct (unique) pos ...
随机推荐
- wps金山文档在线编辑--.Net 接入指南
一.申请成为服务商,对金山文档在线服务进行申请 ①进入官网 https://open.wps.cn/ ②申请后如下图,点击右下角的进入服务 ③申请成功后 ④数据回调URL一定是服务器地址,本次我使用的 ...
- 18 java I/O 系统
流的类继承结构 我们首先看看流的类继承结构,有助于理解下个标签的内容 InputStream OutputStream Reader Writer File类 File类技能表示一个特定文件的名称,又 ...
- English--五大基本句型基本概念
English|五大基本句型基本概念 英语的基本句型是整个英语的框架体系,所以,祝愿看到此文的伙伴们,都可以牢牢掌握! 前言 目前所有的文章思想格式都是:知识+情感. 知识:对于所有的知识点的描述.力 ...
- C# 后台服务器端 Get 请求函数封装
请求参数封装 /// <summary> /// 拼接 Get请求参数 /// </summary> /// <param name="parames" ...
- 老生常谈之js深拷贝与浅拷贝
前言 经常会在一些网站或博客看到"深克隆","浅克隆"这两个名词,其实这个很好理解,今天我们就在这里分析一下js深拷贝和浅拷贝. 浅拷贝 我们先以一个例子来说明 ...
- CRM BP函数
REPORT ZCRM_BP_TEST. """""""""""""& ...
- springboot-发布jar包
其他参考链接: https://www.cnblogs.com/blog5277/p/5920560.html 环境变量配置: 新建系统变量MAVEN_HOME: 在path中添加: ;%MAVEN_ ...
- 记录SQLAlchemy的基本使用
代码 # -*- coding: utf-8 -*- from sqlalchemy import Column, String, create_engine from sqlalchemy.orm ...
- linux初始化shell脚本
#!/bin/bash # this is a init script ping -c 1 -i 0.1 -W 1 baidu.com a=`echo $?` if [ ${a} == 0 ];the ...
- 第十二周LINUX学习笔记
zabbix zabbix-server: 监听的端口10051 zabbix-agent: 10050 Zabbix: Item, Key(键) ethercard.traffic[eth0] ac ...