JS数据结构第一篇---算法之复杂度判断

1、算法：算法是解决特定问题求解步骤的描述，在计算机中表现为指令的有限序列，并且每条指令表示一个或多个操作。

那么一个怎样的算法才能称得上是好算法，也就是说有没有什么标准来评判一个算法的好坏？

在此之前，咱们先来做个试验：

　　用两种方式来实现求裴波那契数列第n项的值，一种方式用递归方式，第二种方式用普通循环方式。

　　在得到结果之前，你猜猜那种方式计算结果更快一些，还是一样快？

　　测试代码如下（JavaScript）：

/**
 * 1、递归实现斐波那契数列：
 * 1,1,2,3,5...  第n项 = 第n-1项 + 第n-2项
 * */
function recursionFbi(n){
    if (n < 3) return 1;
    if (n == 3) return 2;
    // console.log("递归n: ", n);
    return recursionFbi(n-1) + recursionFbi(n-2);
}
 
/**
 * 2、循环实现裴波那契数列
 * 1,1,2,3,5... 第n项 = 第n-1项 + 第n-2项
 * */
function circleFbi(n){
 
    if (n < 3) return 1;
    var a = 1, b = 1, c = 0;
    for (var i = 0; i < n; i++){
        if (i > 1){
            c = a + b;
            a = b;
            b = c;
        }
        console.log("循环i: ", i, ", c: ", c);
    }
    return c;
}

这里输入几个数字做测试，大致记录下结果作对比。

当然每次测试同一个数字的计算时间不一定都相同，跟当前测试的电脑硬件配置，和其他应用同开有一定关系。

当输入n=51的时候，测试结果截图如下：

还有输入其他一些n值的统计数据：

　　上面通过两种方式求裴波那契数列，表现出来的时间损耗值相差惊人！为什么会有这么大的差别？这体现了一个好的算法能让程序的运行效率事半功倍，一个糟糕的算法对于程序来说简直就是灾难！刚才这两种算法方式的区别，等下再分析。

2、现在，我们来说说如何来粗略的估算一个算法的好坏。

　　我们对于算法的设计要求是：正确性、可读性、健壮性、时间效率高、存储量低。

　　因此对于一个算法，我们在运行前，可以从这五个角度来进行判断分析，下面主要从时间效率和存储量角度来细说下：

• 时间复杂度（time complexity）：估算程序指令的执行次数（执行时间）
• 控件复杂度（space complexity）：估算所需占用的存储空间

　　

　　大O表示法是一种粗略的分析模型，能帮助我们快速估算一个算法的执行效率，我们用它来描述算法的时间复杂度。

　　常见的时间复杂度有这些：

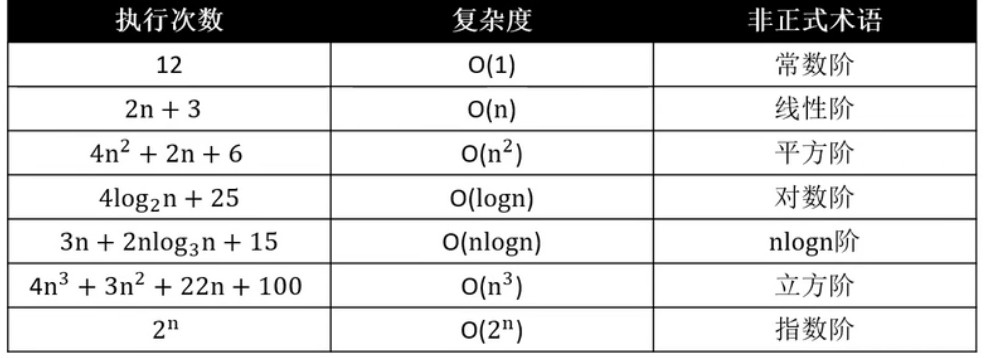
　　在使用大O推导法时，对于常数阶，我们用常数1代替；有多阶项则只保留最高阶项；最高阶项的常数去除。如图：

　　

这里贴上几个示例用来练习时间复杂度的计算（JavaScript）：

//算法复杂度：O(n)
function testCount1(n){
    //指令计数：多个if算作一个指令
    if (n > 10){
        console.log("n > 10")
    }
    else if(n > 5){
        console.log("n > 5")
    }
    else{
        console.log("n <= 5")
    }
 
    //指令计数：1 + n + n + n = 3n + 1
    for (var i = 0; i < n; i++){
        console.log("...testCount1...")
    }
}
 
//算法复杂度：O(logn)
function testCount3(n){
    //指令计数：n/2 = log2(n)
    //n=2 -> 1;  n=4->2;    n = 8->3;   n = 16->4;  n = 32->6
    //1=log2(2); 2=log2(4); 3=log2(8);  4=log2(16);  6=log2(32)
    while((n = n / 2) > 0){
        console.log("***testCount3***");
    }
}
 
//算法复杂度：O(nlogn)
function testCount4(n){
    //指令计数：1 + 2*log2(n) + log2(n) * (1+3n) = 1 + 3log2(n) + 3n*log2(n)
    for (var i = 1; i < n; i = i * 2){
        //1 + 3n
        for (var j = 0; j < n; j++){
            console.log(">>>testCount4>>>")
        }
    }
}
 
//算法复杂度：O(n^2)
function testCount2(n){
    //指令计数：1 + 2n + n * (1+3n) = 1 + 3n + 3n^2 = 3n^2 + 3n + 1
    for (var i = 0; i < n; i++){
        for (var j = 0; j < n; j++){
            console.log("...testCount2...")
        }
    }
}

常见的时间复杂度所耗时间的大小排列如下：

3、掌握了大O推导法，我们用大O表示法来论证本文最开始计算裴波那契数列的两种算法的区别：

　3.1 递归方式算法，先看下图：

　　

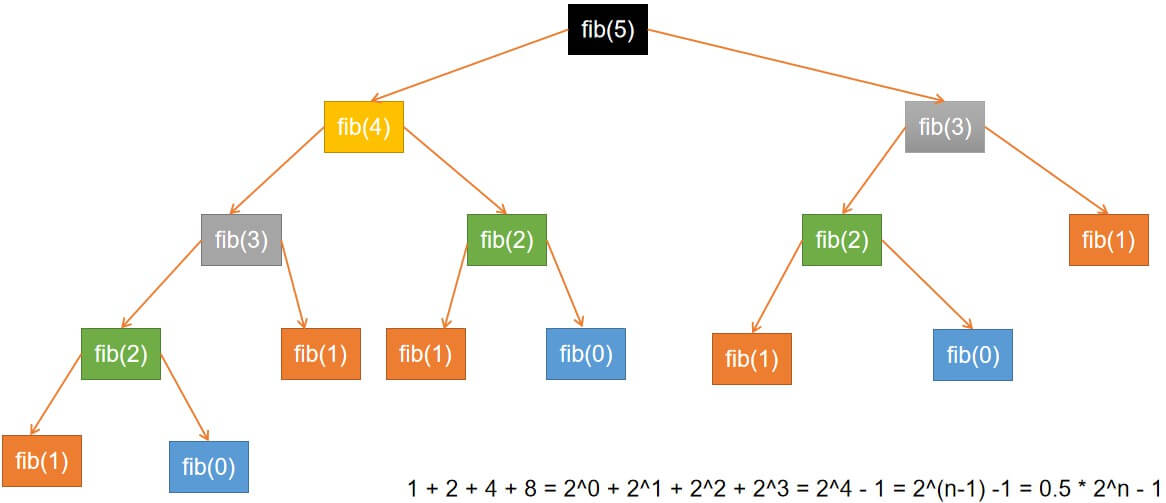
　　可以得出，这里的递归方式算法用大O表示法来表示，它属于指数阶，可以粗略表示为：O(n) = 2^n

　　3.2 而第二种循环方式算法为线性阶的，用大O表示法为：O(n) = n

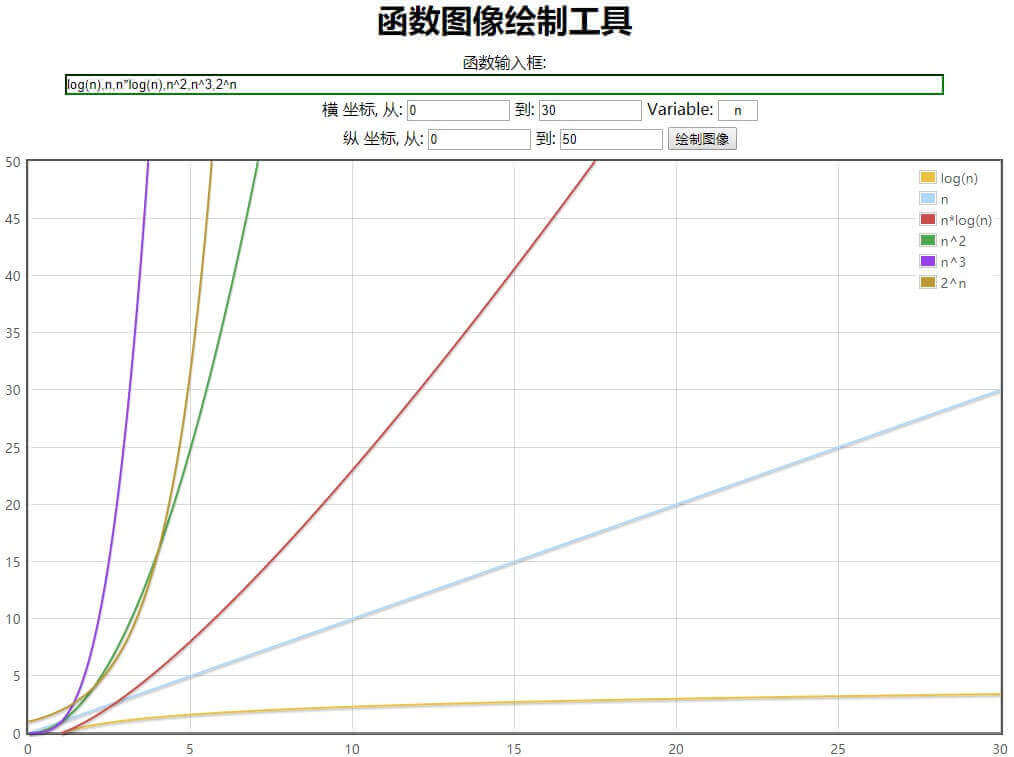
　　3.3 我们对比一下指数阶和线性阶的函数曲线图就知道，n系数越大，这两种方式的最后的结果相差越大。

　　　　所以当n越大时，递归方式算法的计算次数呈指数级上升，最后次数结果越大，时间损耗数也就越多。

测试Demo地址：https://github.com/xiaotanit/Tan_DataStruct