图论 --- 骑士周游问题,DFS

A Knight's Journey

 

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 28630		Accepted: 9794

Description

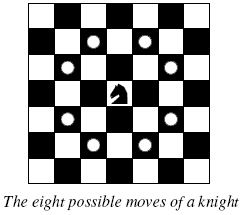
Background
The knight is getting bored of seeing the same black and white squares again and again and has decided to make a journey

around the world. Whenever a knight moves, it is two squares in one
direction and one square perpendicular to this. The world of a knight is
the chessboard he is living on. Our knight lives on a chessboard that
has a smaller area than a regular 8 * 8 board, but it is still
rectangular. Can you help this adventurous knight to make travel plans?

Problem

Find a path such that the knight visits every square once. The knight can start and end on any square of the board.

Input

The
input begins with a positive integer n in the first line. The following
lines contain n test cases. Each test case consists of a single line
with two positive integers p and q, such that 1 <= p * q <= 26.
This represents a p * q chessboard, where p describes how many different
square numbers 1, . . . , p exist, q describes how many different
square letters exist. These are the first q letters of the Latin
alphabet: A, . . .

Output

The
output for every scenario begins with a line containing "Scenario #i:",
where i is the number of the scenario starting at 1. Then print a
single line containing the lexicographically first path that visits all
squares of the chessboard with knight moves followed by an empty line.
The path should be given on a single line by concatenating the names of
the visited squares. Each square name consists of a capital letter
followed by a number.

If no such path exist, you should output impossible on a single line.

Sample Input

3
1 1
2 3
4 3

Sample Output

Scenario #1:
A1

Scenario #2:
impossible

Scenario #3:
A1B3C1A2B4C2A3B1C3A4B2C4

【题目背景】
我们知道，在国际象棋中, 骑士的移动路线是 L 型的, (在水平和垂直两个方向上, 一个方向上走两格, 另一个方向上走一格). 因此, 在一个空棋盘中间的方格上, 骑士
可以有 8 种不同的移动方式.
这题的问题是：如果马从[0,0]出发，能否将棋盘中的每一个格子走遍并且保证每个格子直走一次，如果可以的话，按照字典序输出路径。

【题目分析】
这题其实就是一个简单的DFS，难点在于按照字典序来输出路径，这就需要自己画图分析了。

下面是我的AC代码：

#include<iostream>
#include<cstring>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
using namespace std;
bool vis[][];  //标记是否走过
int path[][];   //记录走过路径
bool Find;
int a,b;
int dir[][]={-,-,  -,,  -,-,  -,,  ,-,  ,,  ,-,  ,};  //实际是一个闭合的环
void dfs(int i,int j,int k)
{
    if(a*b==k)
    {
        for(int i=;i<k;i++)
        {
            printf("%c%d",path[i][]+'A',path[i][]+);
        }
        puts("");
        Find=;
    }
    else
    {
        for(int x=;x<;x++)
        {
            int n=i+dir[x][];
            int m=j+dir[x][];
            if(n>=&&n<b&&m>=&&m<a&&!vis[n][m]&&!Find)
            {
                vis[n][m]=;
                path[k][]=n;
                path[k][]=m;
                dfs(n,m,k+);
                vis[n][m]=;
            }
        }
    }
}
int main()
{
    int kase=;
    int T;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d%d",&a,&b);
        Find=;
        memset(vis,,sizeof(vis));
        vis[][]=;
        path[][]=;
        path[][]=;
        printf("Scenario #%d:\n",kase++);
        dfs(,,);
        if(!Find)
           printf("impossible\n");
        puts("");
    }
    return ;
}