移相器——K波段有源移相器设计

博主之前在做一款K波段有源移相器，所用工艺为smic55nmll工艺，完成了几个主要模块的仿真，现对之前的工作做个总结。

K波段的频率范围是18G——27GHz，所设计移相器的工作频率范围是19G——24GHz。其基本结构和我前面发布的一篇随笔类似，只不过用了45nm的工艺。

首先是正交信号产生电路，分别仿真了两种结构，即RC结构（图1）和RLC结构（图2）。

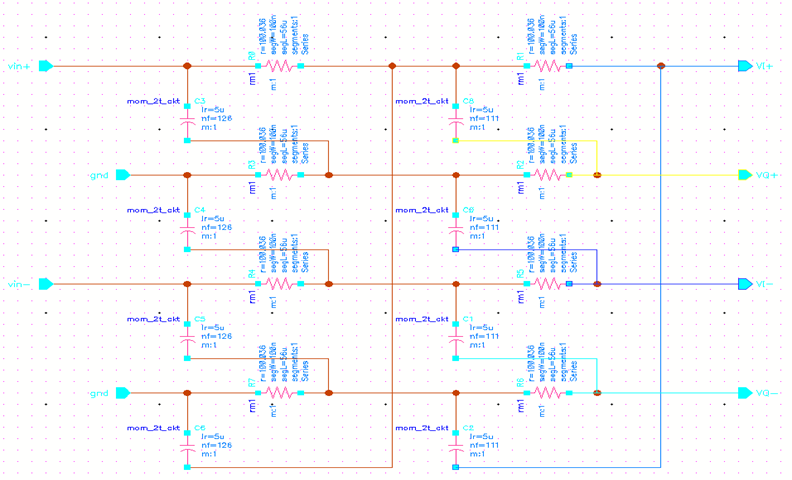
图1 RC结构正交信号产生电路

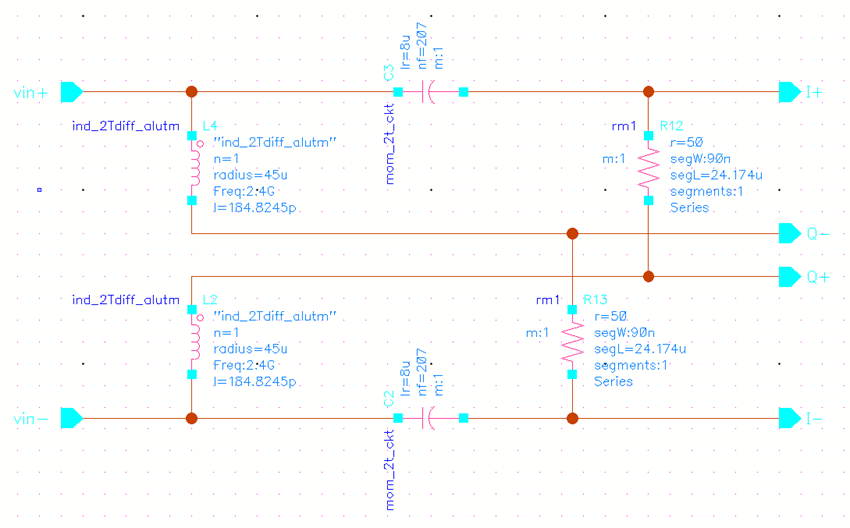
图2 RLC结构正交信号产生电路

经过仿真发现，RC电路和RLC电路都能产生近乎无误差的四路正交信号，如图3和图4 所示。

图3 RC结构相位仿真

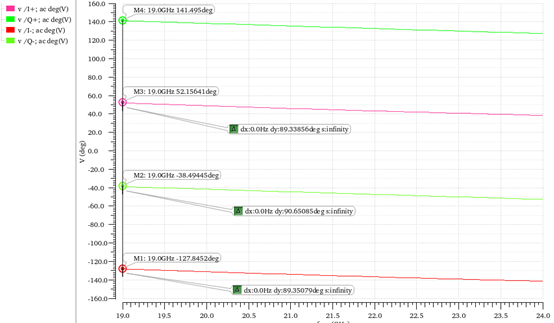
图4 RLC结构相位仿真

但是，RC结构的增益损失交大，RLC增益损失较小，增益曲线如图5和图6所示。

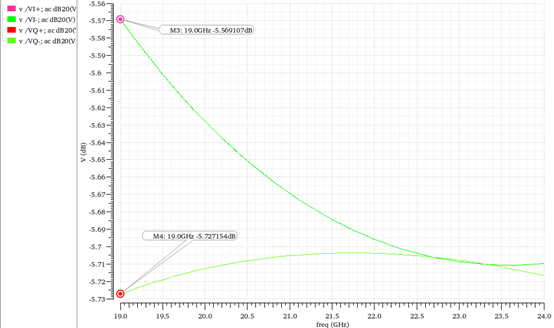
图5 RC结构增益仿真

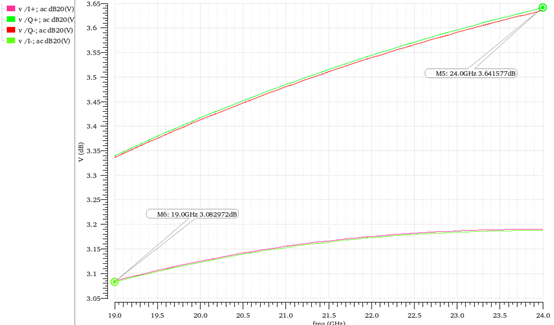
图6 RLC结构增益仿真

我们的指标要求里还有温度范围的要求，即-50°C——125°C的范围，经仿真发现，RC结构的正交信号精度受温度影响较小，RLC结构的正交信号精度受温度影响较大，故本设计采用RC结构，其瞬态仿真如图7。

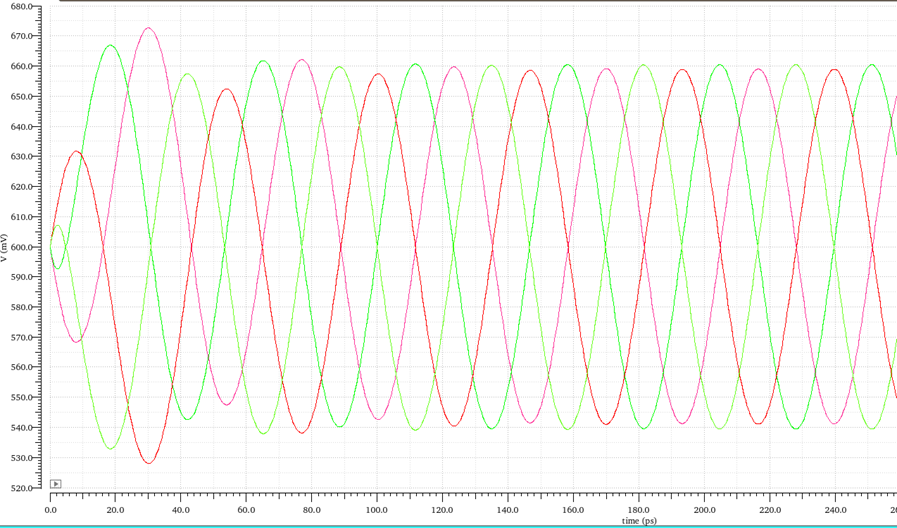
图7 RC结构瞬态仿真结果

接下来是吉尔伯特单元，即矢量合成单元，电路结构如图8所示，其中为了扩大带宽，采用了电感峰化技术。

图8 吉尔伯特单元电路结构

目前用理想的电流源代替DAC幅度调制部分的电流镜，方便仿真，真实结构如图9所示。

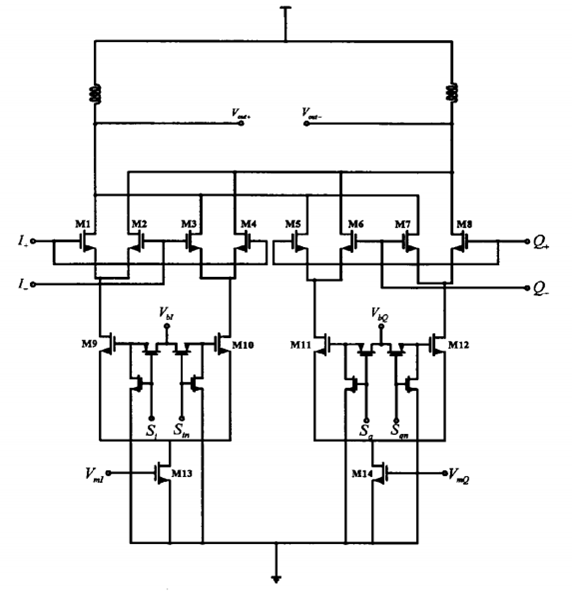
图9 吉尔伯特单元电路结构（加MOS开关）

对于DAC幅度调制模块，设计如图10所示。其中电流由NMOS入，传到PMOS，采用共源共栅电流镜，可以减小衬偏效应。通过开关选择电流流入到I通路还是Q通路，从而控制输出信号幅度。尾部的NMOS开关用来选择极性，即四个象限，11代表第一象限，01代表第二象限，00代表第三个象限，10代表第四个象限。

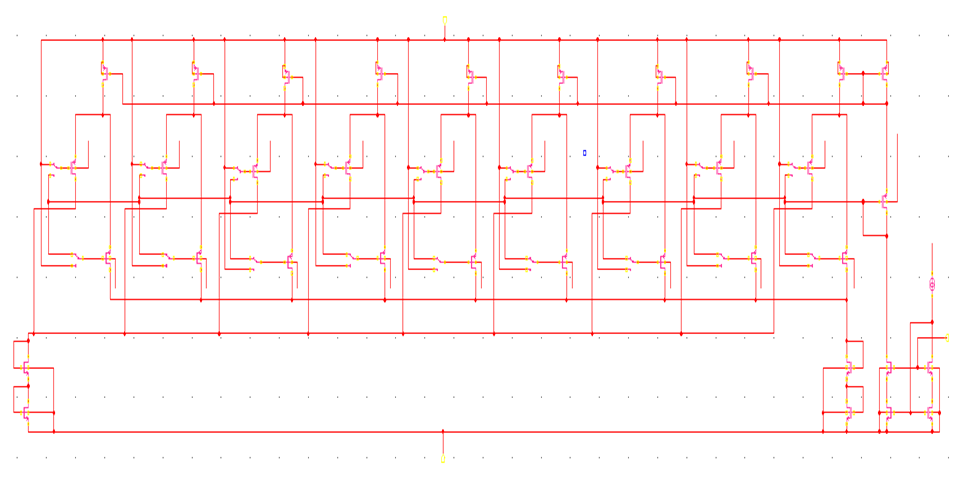
图10 DAC幅度调制模块

首先，通过吉尔伯特单元的带宽，如图11所示，可以看到带宽远远满足要求，接着仿真了第一象限的相位，如图12所示，最后，仿真了360°的相位变化，如图13所示。

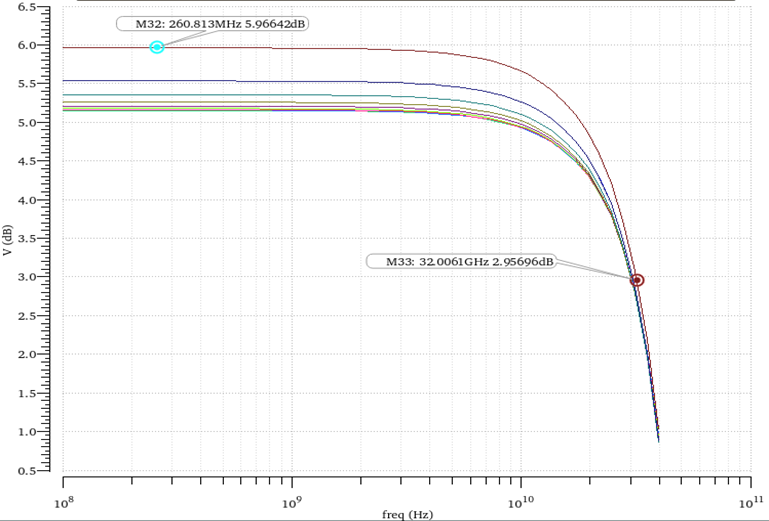
图11 吉尔伯特单元的带宽

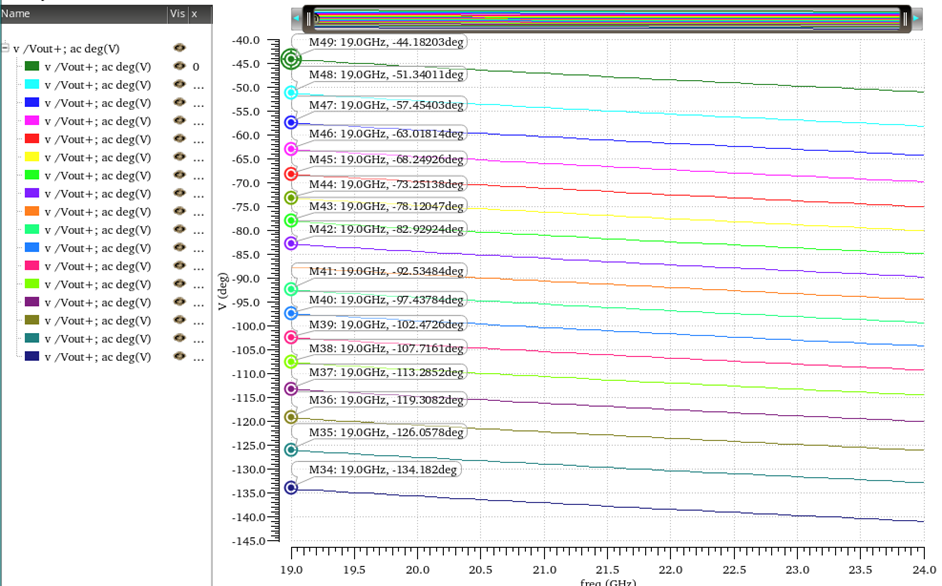
图12 第一象限相位仿真

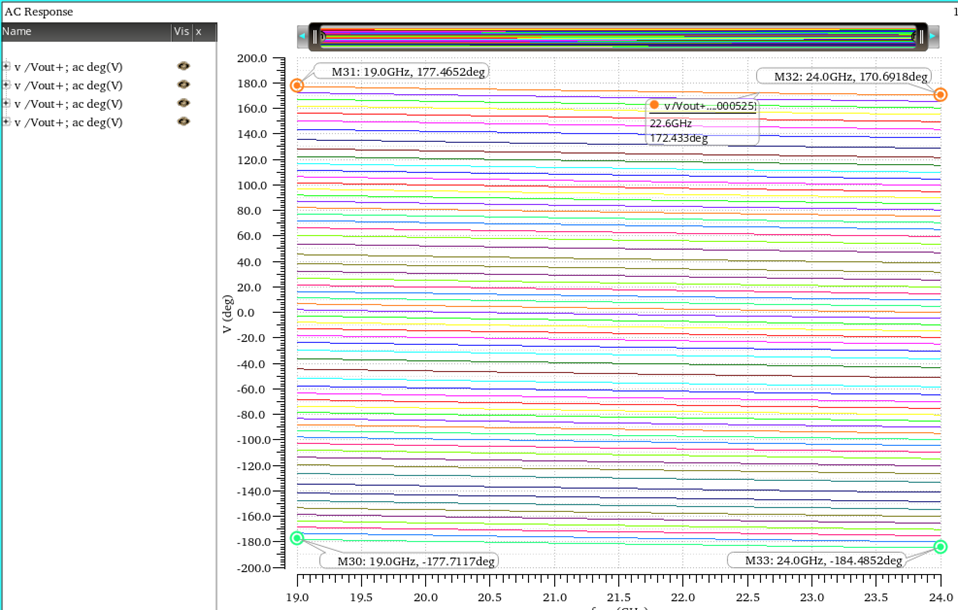
图13 360°相位仿真

现在基本的模块已经搭建完毕，360°的相移也可以实现，基本功能完成，但是还要考虑输入输出巴伦，其作用是匹配和单端差分的转换，在这里不作考虑。

最后要给出的是开关的真值表，利用该真值表可以完成数字控制，如表1和表2所示。真值表基本采用one-hot编码方式（忽略转变极性的开关）。

表1 0到180°的开关控制真值表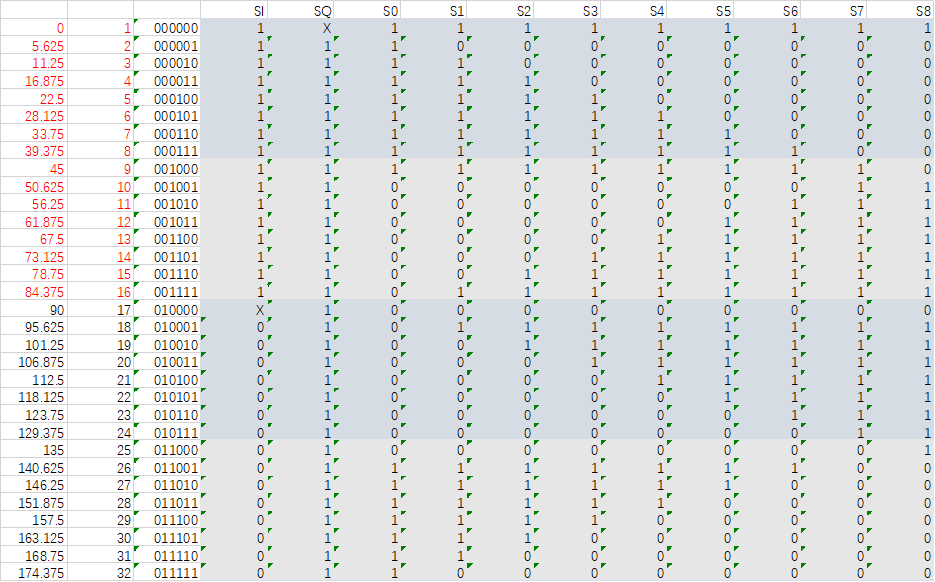

表2 180°到360°的开关控制真值表

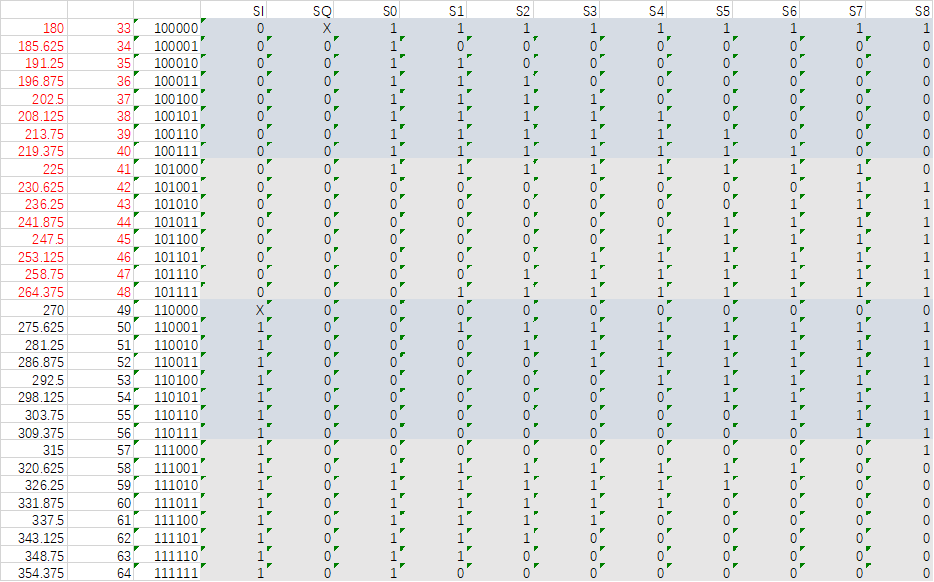
考虑到每次开关切换，如果按照上述真值表，那么每次可能会改变两个相位及以上相位，造成移相误差及不必要的功耗，故采用格雷码完成开关电路设计。真值表如表3和表4所示。

表3 0到180°的开关控制真值表（格雷码）

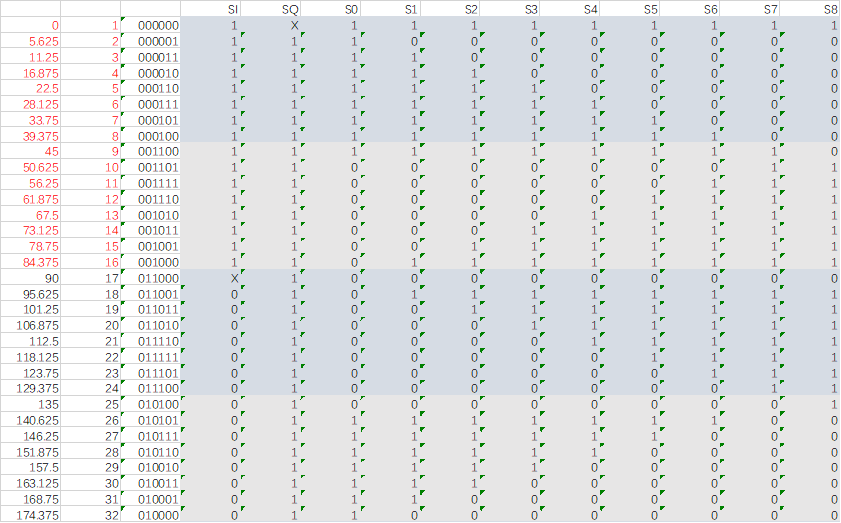
表4 180°到360°的开关控制真值表（格雷码）

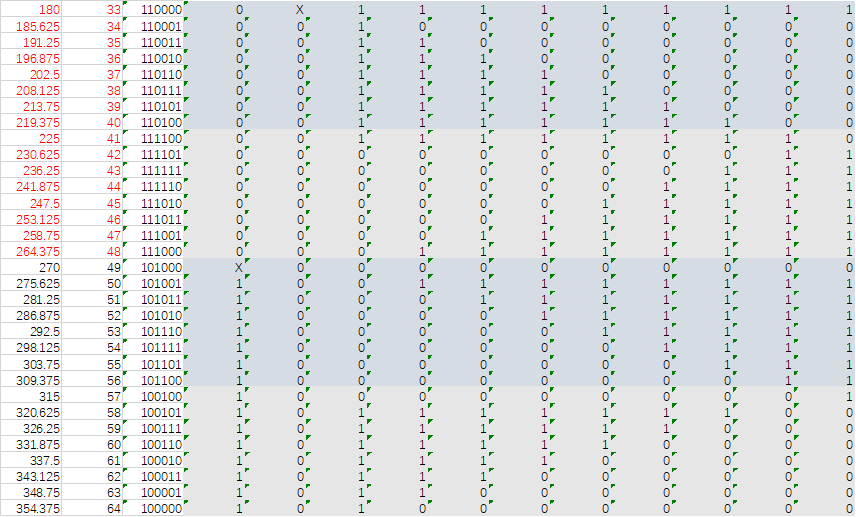
　　基本模块搭建完成。以上便是我的工作总结。