Matlab:Toeplitz矩阵-向量乘法的快速傅里叶(FFT)算法

一、$\tt Toeplitz$矩阵与循环（$\tt Circulant$）矩阵

定义

为$n\times n$阶循环矩阵。

定义 $T_n(i,j)=t_{j-i} $  为$n\times n$ 阶$\tt Toeplitz$矩阵

通过令矩阵$B_n＝$

从而构造出$2n\times 2n$阶循环矩阵

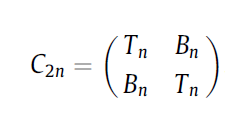
假设有一$n\times 1$阶列向量$\bf u$

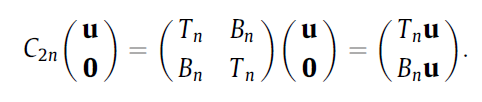
其中，$C_{2n}$可以由快速傅里叶对角化

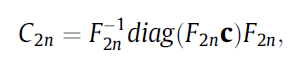
其中$\bf c$表示$C_{2n}$矩阵的第一列元素，$\bf F$ 表示快速傅里叶($\tt fft$)变换，$\bf F^{-1}$ 表示快速傅里叶($\tt ifft$)逆变换。进一步可写成

因此，计算$\bf T_n u$等价于计算

查阅文献我们知道，直接计算$\bf T_n u$的存储量和计算量分别为$O(n^2)$和$O(n^3)$,但是利用快速傅里叶计算可以将存储量和计算量分别降为$O(n)$和$O(n \log_2 n)$.

从以下数据可以更直观的看出FFT显著的优点

 二、数值应用

• 考虑一维椭圆方程

$$－\Delta u=f(x),\qquad a<x<b,\tag{1}$$

满足齐次$Dirichlet$边界条件。

对$x\in [a,b]$一致网格剖分：$a=x_0<x_1,\cdots,x_M=b$,$h=\frac{b-a}{M}$。$U,u$分别表示数值解和真解。应用二阶中心差分逼近二阶导数

$$\Delta u(x_i)= \frac{u(x_{i-1})-2u(x_i)+u(x_{i+1}) }{h^2}+O(h^2).\tag{2}$$

由(2)式可得求解方程(1)的数值格式的矩阵形式

$$A{\bf U}＝\widehat{f}.\tag{3}$$

其中

$$A=\tt －\frac{1}{h^2}toeplitz([-2,1,zeros(1,M-3)]),$$

$$\widehat{f}=(   f(x_1),f(x_2),\cdots,f(x_{M-1})   )^T.$$

$${\bf U}=(u_1,u_2,\cdots,u_{M-1})^T.$$

• 考虑二维椭圆方程

$$－\Delta u=f({\bf x,y}),\qquad {(\bf x,y)}\in (a,b)\times (c,d),\tag{4}$$

对$x\in [a,b]$一致网格剖分：$a=x_0<x_1,\cdots,<x_{M_1}=b$,$h_1=\frac{b-a}{M_1}$，$c=y_0<y_1,\cdots,<y_{M_2}=d$,$h_2=\frac{d-c}{M_2}$。$U,u$分别表示数值解和真解。应用二阶中心差分逼近二阶导数

$$\Delta u(x_i,y_j)= \frac{u(x_{i-1},y_j)-2u(x_i,y_j)+u(x_{i+1},y_j) }{h_1^2}+ \frac{u(x_i,y_{j-1})-2u(x_i,y_j)+u(x_i,y_{j+1}) }{h_2^2}+O(h_1^2+h_2^2).\tag{5}$$

由(5)式可得求解方程(4)的数值格式的矩阵形式

$$A{\bf U}＝\widehat{f}.\tag{6}$$

其中

$$A_1=\tt toeplitz([-2,1,zeros(1,M_1-3)]),$$

$$A_2=\tt toeplitz([-2,1,zeros(1,M_2-3)]),$$

$$ A_x = -\tt \frac{1}{h_1^2} I_{M_2-1}  \bigotimes  A_1 ,\mbox{(非toeplitz矩阵)}$$

注意到：

$$  I_{M_2-1}  \bigotimes  A_1U = reshape\Big( A_1 reshape( U,M_1-1,M_2-1 ),( M_1-1 )(M_2-1),1 \Big). $$

$$ A_y = -\tt \frac{1}{h_2^2}  A_2 \bigotimes I_{M_1-1} ,$$

$$A = A_x+A_y,$$

$$\widehat{f}=(   f(x_1,y_1),f(x_2,y_1),\cdots,f(x_{M_1-1},y_1) , f(x_1,y_2),f(x_2,y_2),\cdots,f(x_{M_1-1},y_2), \cdots\cdots, f(x_1,y_{M_2-1}),f(x_2,,y_{M_2-1}),\cdots,f(x_{M_1-1},,y_{M_2-1}) )^T.$$

$${\bf U}=(u_{1,1},u_{2,1},\cdots,u_{M_1-1,1},u_{1,2},u_{2,2},\cdots,u_{M_1-1,2},\cdots\cdots,u_{1,M_2-1},u_{2,M_2-1},\cdots,u_{M_1-1,M_2-1})^T.$$

 由数值格式（3），（6）显然可知，当空间网格剖分很大时，矩阵乘法的计算量将会十分昂贵，因此利用FFT算法是很有必要的。接下来介绍一种有效的线性迭代法-共轭梯度法（CGS）

三、数值例子

• case $I$(1D) ： 真解：

$$ u = \sin(x),\qquad x\in( 0,\pi ), $$

分别应用直接法和FFT方法的实验结果见下图

• case $II$(2D) ： 真解：

$$ u = \sin(x)\sin(y),\qquad (x,y)\in( 0,\pi )^2, $$

分别应用直接法和FFT方法的实验结果见下图

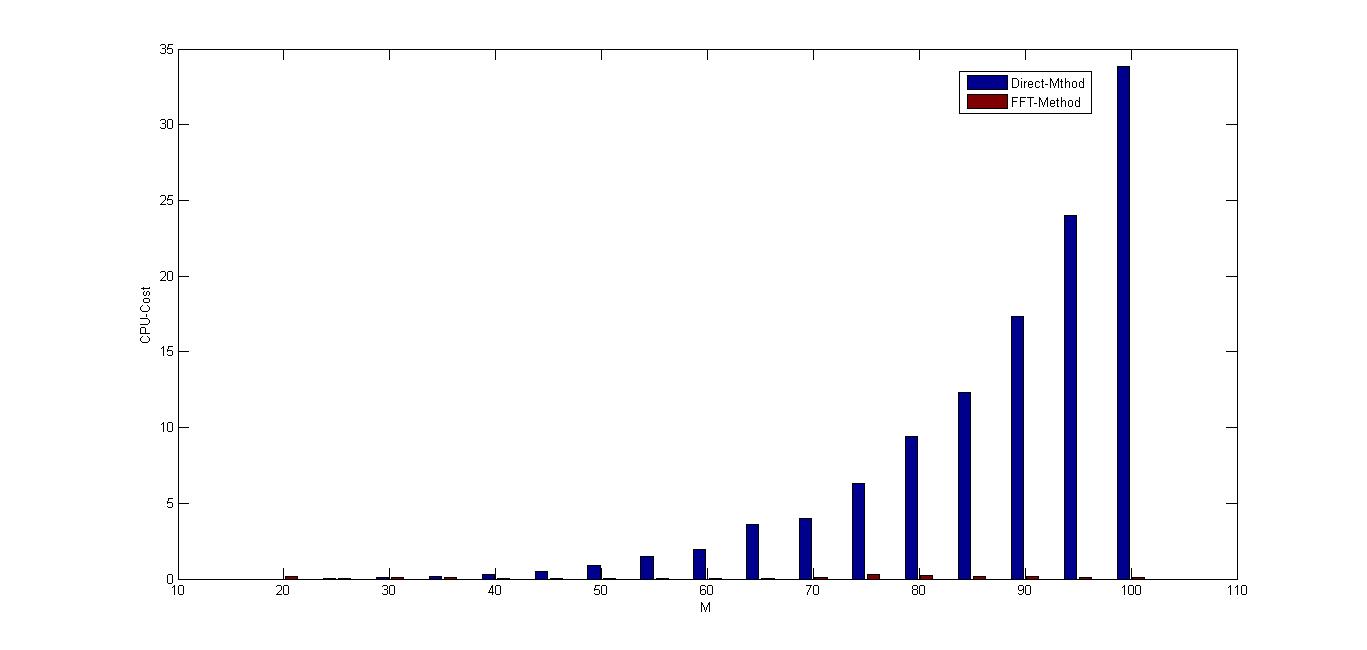
从数值实验结果可以直观的看出，FFT的计算效率是惊人的！