CF98C Help Greg the Dwarf 题解

CF98C Help Greg the Dwarf 题解

为什么不三分？

首先我们考虑如何求出答案。

如图，考虑设夹角为 \(\theta\)，那么可以得到表达式：

\[[\cfrac a {\tan \theta} - (l \cos \theta - b)] \sin \theta
\]

整理可得：

\[a \times \cos\theta + b \times \sin\theta - l \times \sin \theta \cos \theta
\]

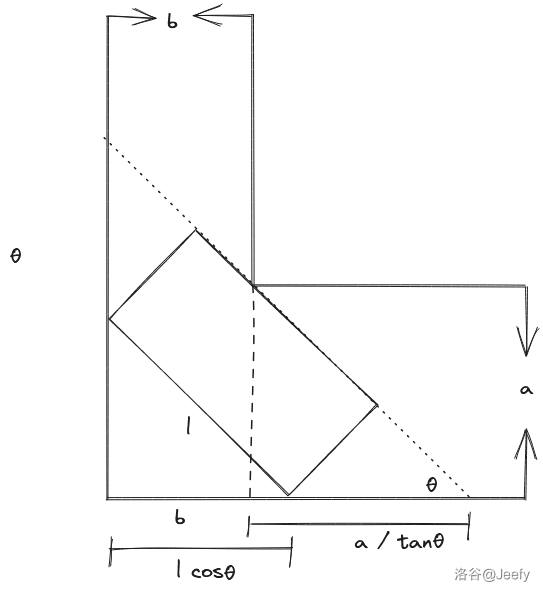
于是可以考虑观察这个函数的单调性：

明显这是个单峰函数。

考虑合法的大小即是此函数的最小值。

特判掉 \(l \le b\) 或者 \(l \le a\) 的情况：

• \(l \le b \implies w = \min(a, l)\)

• \(l \le a \implies w = \min(b, l)\)

所以考虑三分答案求最小即可。

不过需要判断无解的情况！

注意一下 CF 上似乎不能使用 long double……亦或是我写法的问题 QwQ

#include <stdio.h>
#include <math.h>
#define ldb double

int a, b, l;
ldb calc(ldb theta) {
    ldb c = cos(theta), s = sin(theta);
    return a * s - l * c * s + b * c;
}

int main() {
    scanf("%d %d %d", &a, &b, &l);

    if (l <= b) {
        printf("%.10lf\n", (ldb)(a < l ? a : l));
        return 0;
    }

    if (l <= a) {
        printf("%.10lf\n", (ldb)(b < l ? b : l));
        return 0;
    }

    ldb L = 0, R = acos(-1) / 2;
    const ldb eps = 1e-10;
    while (L + eps < R) {
        ldb ml = (L + L + R) / 3, mr = (L + R + R) / 3;
        ldb vl = calc(ml), vr = calc(mr);

        if (vl < vr) R = mr;
        else L = ml;
    }

    ldb ans = calc(L);

    if (l < ans) ans = l;

    if (ans < eps) puts("My poor head =(");
    else printf("%.10lf\n", ans);

    return 0;
}