虹科案例｜虹科Visokio商业智能平台在疫后帮酒店业打好翻身仗！

疫后时代以来，报复性度假呈爆炸式增长，首先点燃的就是酒店行业。面对疫后更为理性“挑剔”的客户以及酒店行业复苏节点：

如何提升酒店管理效率？

怎么准确判断流量变化趋势，拓展线上客源？

有没有可能通过云科技手段，加强互联网深度使用，实现酒店智能化、互联化？

类似问题似乎是当下无数酒店行业企业亟需解答的困惑。虹科Visokio Omniscope绝不能容忍任何酒店企业在疫后复苏黄金期掉队！下面虹科将以酒店行业为例，以其相关数据为基础，主要从数据探索、数据预处理、数据分析三个部分，为大家详细介绍虹科提供的Visokio，作为一款商业智能和数据分析平台，可以如何从数据到分析再到可视化，为企业提供一套完整的解决方案，帮助企业抢得先机，跑得更快！

一．数据探索

该表共包含119390条数据，含32个字段。由于源数据表字段是英文的，不太符合国人的阅读需求，因此需要先进行数据探索，将其转换为中文，以便于更好地理解各字段的含义。

将数据集导入到MySQL数据库后，各字段的名字、类型、长度等性质都被做了重新整理，设计后的表结构如下图所示：

编辑搜图

请点击输入图片描述（最多18字）

编辑搜图

请点击输入图片描述（最多18字）

二．数据预处理

1.输入数据

首先，在虹科Visokio Omniscope中构建一个新的项目，用于处理酒店预订数据的工作流。然后，添加一个数据库输入块，通过JDBC，将MySQL数据库中的“酒店预订源数据”表连接到虹科Visokio Omniscope。最后，查看表中数据的分布情况：

我们可以发现`下单公司`该字段值存在明显缺失，NULL值比例达到了94.31%。其次，“旅行社”字段也存在大量NULL值，比例达到13.69%。

因此，我们之后需要着重对这两个字段值进行处理。另外，由于客户抵达酒店的日期被切分为年、月、周、日四个字段进行存储，所以为方便后续的使用，需要将其合并起来形成一个完整的日期。

2.重复值处理

由于数据源已经做了脱敏处理，所以没有包含任何客户或酒店的敏感信息，原始数据表中也不存在主键或订单ID等标识，即使2条记录完全一样，也不一定就是重复的。因此该处不对“重复记录”进行删除。

3.缺失值处理

（1）“下单公司”字段

由于该字段缺失率达到了94%，并且值的分布较为零散，不存在分布趋势，因此可以认为该字段参考价值较低，可直接将其删除。

（2）“旅行社”字段

该字段值已经作了脱敏处理，使用ID代表各个旅行社。虽然字段存在大量缺失，但存在合理性，因为客户可以自行预订酒店，并不一定需要通过旅行社进行预订。于是，使用ID=0填充空值，代表该记录没有旅行社ID。

（3）“儿童数”字段

浏览全表，发现在将近12万条记录中，只有4条记录的“儿童数”字段值缺失。作为int数值型变量，可采用中位数进行补齐。

（4）“旅客国籍”字段

在该字段的所有值中，旅客国籍都用了国家的三字母代码表示，不过可以发现其中有488条记录值为NULL，故采用众数PRT进行填充。

4.异常值处理

（1）“餐类型”字段

该字段虽然没有缺失值，但是观察数据分布，发现有1169条数据字段值为“Undefined”，即未定义，占比0.98%。另外，该分类字段有一个类别是’SC’，即无餐。因此，可以把“Undefined”修正为“SC”。

（2）“市场细分”字段和“分销渠道”字段

与用餐类型相似，通过数据分布情况发现`市场细分`字段存在2条记录字段值为“Undefined”，分销渠道`字段存在5条记录字段值为“Undefined”。作为分类字段，此处使用众数来进行修正。

（3）入住人数统计

在一个订单中，入住人数必须大于0，因此筛选出订单入住总人数为0的记录，即成人数、儿童数、婴儿数均为0，共180条记录，将其进行删除。不同地方有不同规定，此处不考虑未成年人订酒店的问题，因此不对成年人数为0的记录做处理。

（4）“平均每日费用”字段

该字段不存在缺失值，但是存在异常值。对于每日的开销，数据范围应是大于等于0，因此需要删除开销为负的记录，共1条。其次，所有的记录中数据均分布在0-520之间，存在一条值为5400的记录，可以认为这是离群值，会严重影响后期的聚合统计，因此将离群记录删除。

（5）入住天数为0

在一个订单中，客人预订房间入住的天数应大于0，否则认定为没有预订房间。因此入住总天数为0的异常记录需要被删除，即删除周末和工作日入住天数均为0的记录，此处共删除645条记录。

（6）“旅客国籍”字段

在该字段中，同时存在两个表示中国的值，即CN和CHN，为方便后续表连接，此处将CN修正为CHN。此外，该字段还存在值TMP，在国家代码记录表中查询不到，为错误值，并且占比较小，仅为3条记录，因此直接将其删除。

5.字段值汉化

数据表中的分类字段，值均为英文，为便于阅读，将字段值替换为中文。

6.日期值处理

（1）入住日期处理

前面提到在该数据表中，客人预订的入住时间被切分为了年、月、周、日四个字段。为方便后续的操作和阅读，在此处需要将年、月、日三个字段合并起来，形成一个日期形式的字段值，新字段命名“预订入住日期”，输出模式设置为“yyyy-MM-dd”。

（2）“订单最后更新日期”

原始数据表中订单最后更新日期为字符型，需将其改为日期型，输出模式设置为“yyyy-MM-dd”。

在便于阅读Visokio Omniscope中完成上述所有的数据预处理，形成工作流如下：

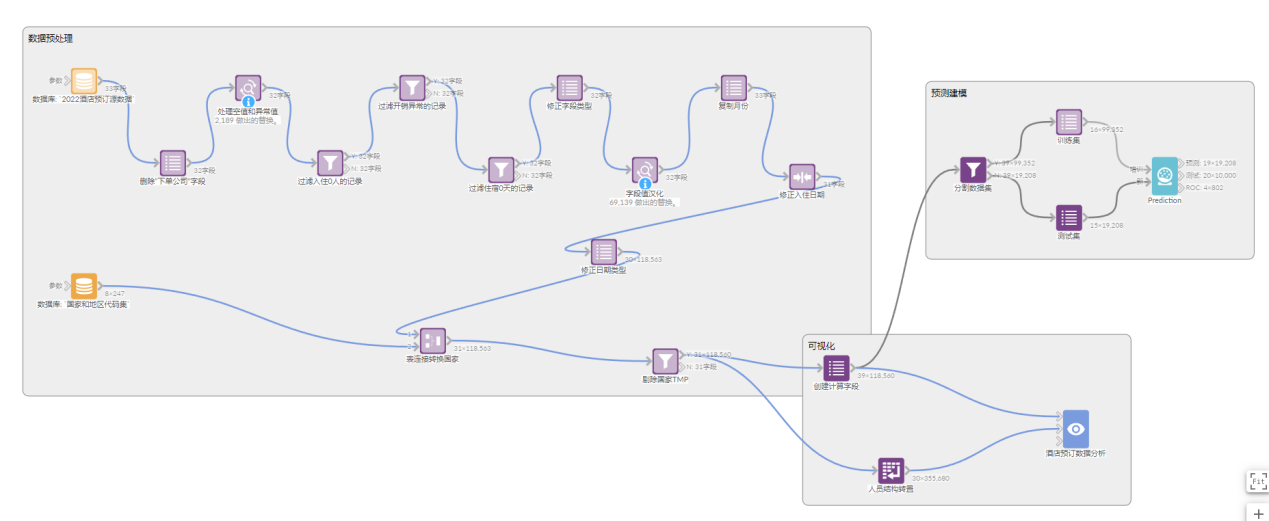编辑搜图

请点击输入图片描述（最多18字）

三．数据分析

1.数据分布情况

首先可以对原始数据集中比较重要的字段数据分布做一个可视化处理，以便大家快速知道数据集中包含的信息以及各字段数据的分布情况，构建出第一个仪表板-数据的分布情况，如下图所示：

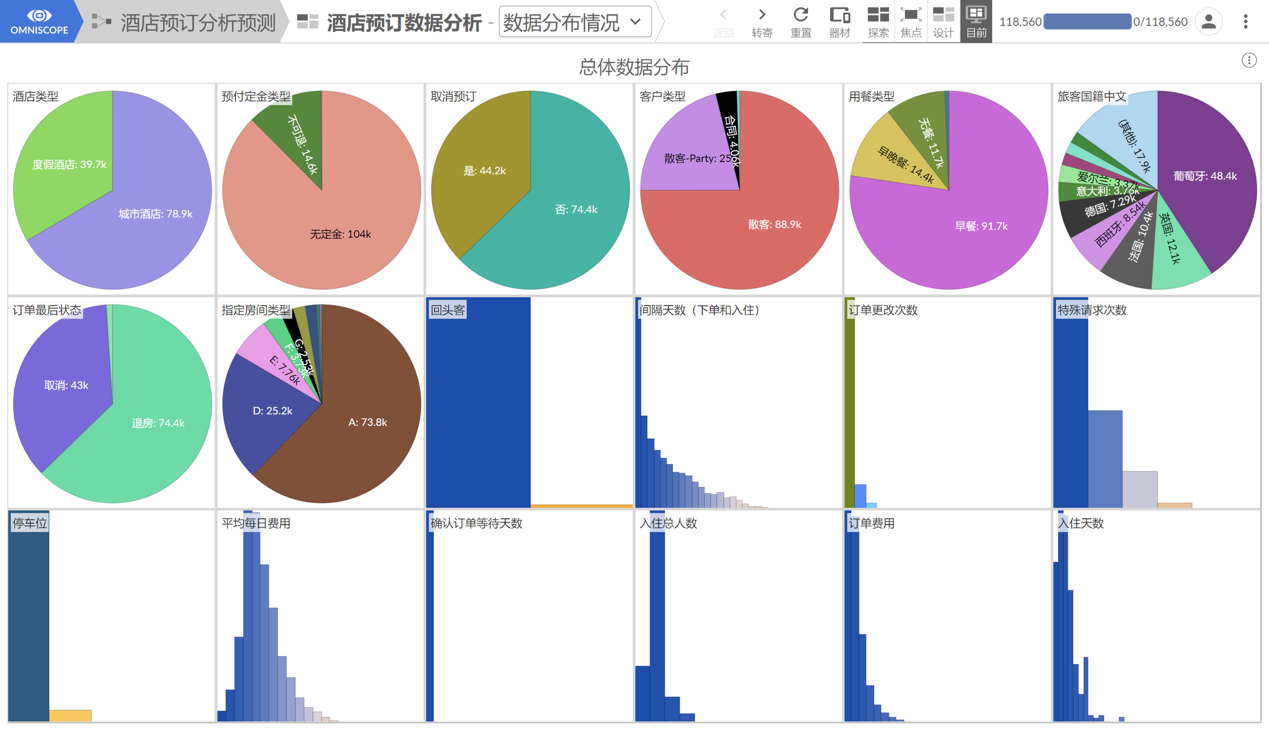编辑搜图

请点击输入图片描述（最多18字）

从上图可以了解到，在总体数据中，城市酒店和度假酒店的订单记录约为2：1，相差较大。因此在之后分析的过程中，应注重特征分布和比率，而不是值的大小。

其次，绝大多数的订单都不需要提前交定金，但在需要交定金的14.6k个订单中，只有162条订单定金是可退的，这暗示了消费者为避免造成不必要的损失，在预付定金时需要慎重考虑。

再者，对于订单的取消情况，总体的取消率达到了37%，后期需要对取消情况进行着重分析。

对于数值型变量，通过直方图可以了解到：

大部分旅客都不会有特殊请求，约有94%的订单显示旅客不需要停车位。此外，在入住总人数上，基本在1-4人的区间内，显示入住2人的比例最高，达到了68.87%。而入住天数大多在1-4天的区间内，显示预订入住2天的比例最高，达到了23.31%。

2.酒店数据分析

源数据中的酒店类型有两种：度假酒店和城市酒店。考虑到这两个酒店类型本身性质不同，且记录数相差较大，因此在分析过程中将数据分为两个类别进行独立分析，并且在仪表板中设置了过滤器，通过过滤器可以筛选出对应类别的数据。

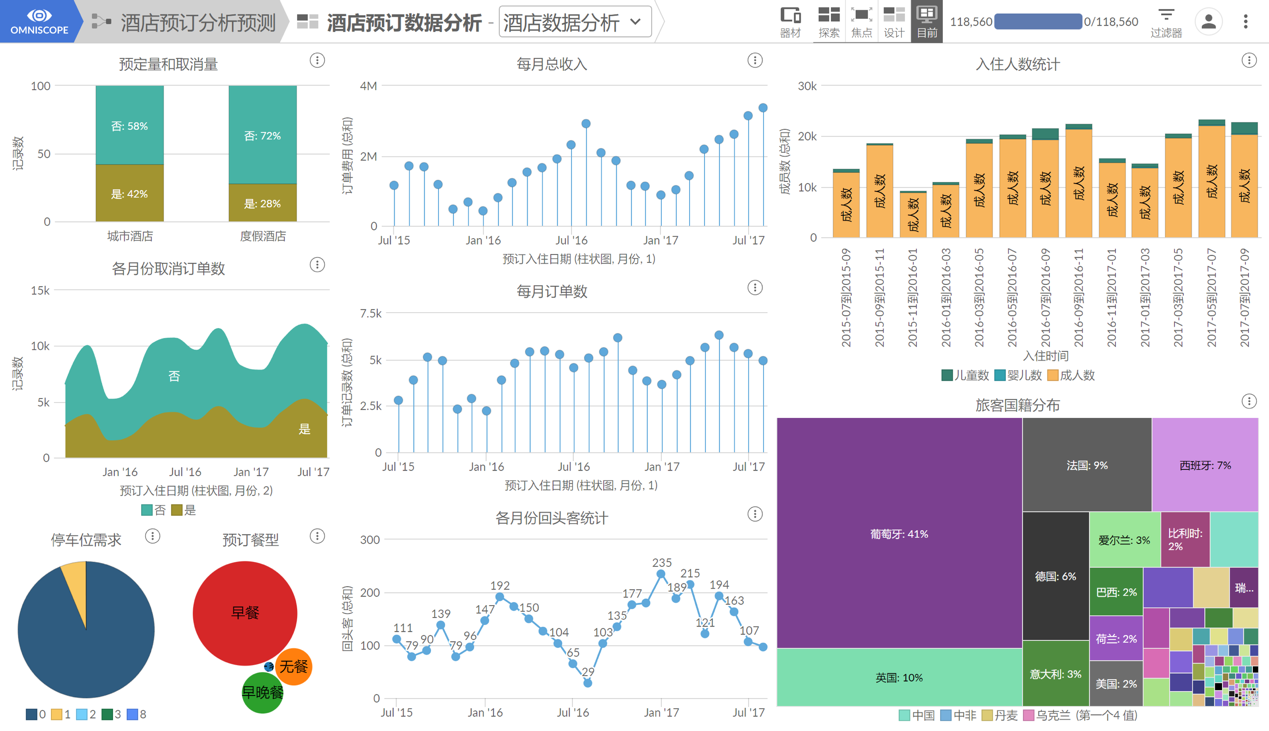编辑搜图

请点击输入图片描述（最多18字）

为提升订单的入住率，酒店需要不断优化自己的服务，给顾客提供更舒服的体验。因此，从酒店运营角度考虑，主要研究:整体的订单情况、订单的取消率、以及可能造成订单取消的因素等等，并做出以下分析（以城市酒店数据为例）：

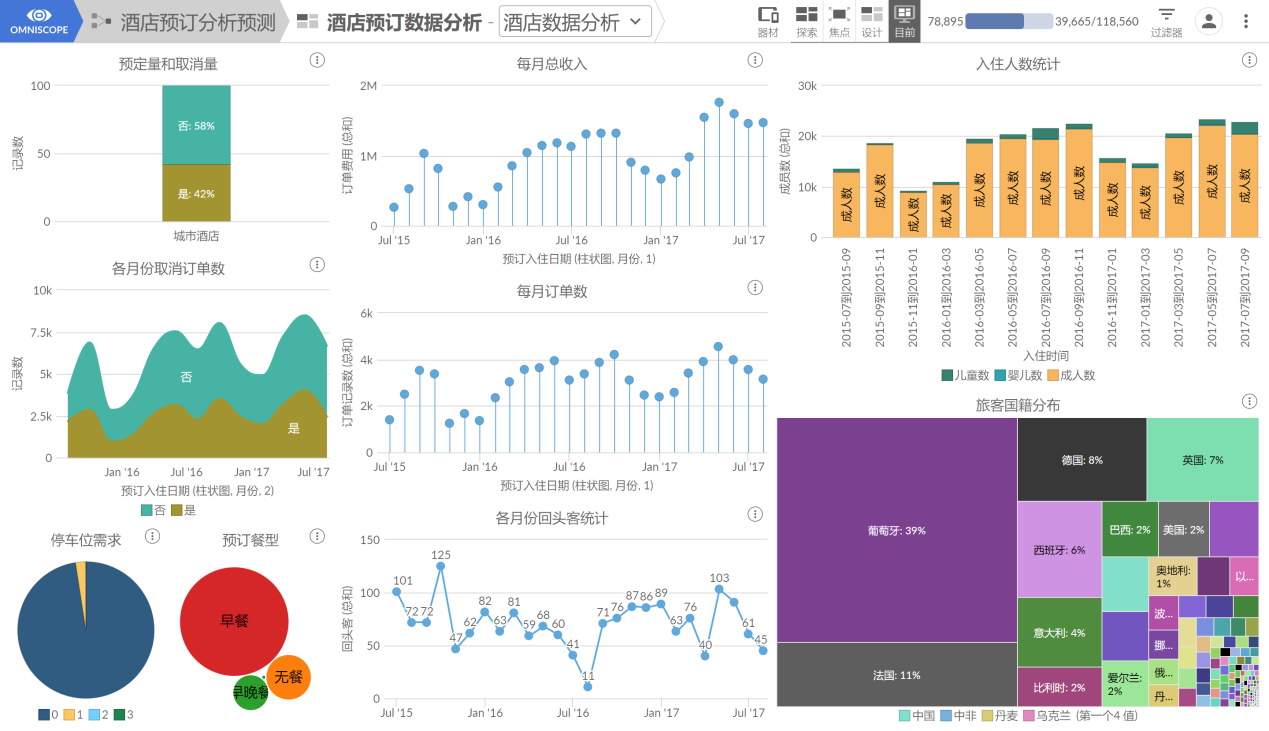编辑搜图

请点击输入图片描述（最多18字）

第一，处理后的数据集中，共有78895条城市酒店的预订数据。通过100%堆叠条形图可以看到，城市酒店的所有订单取消率为42%，这说明客户预订订单后，行程还是存在很大的不确定性。

在此基础上，对各个月份的订单量和取消情况进行分析，绘制“各月份取消订单数”面积图。可以发现，订单取消量随时间变化的趋势与总体订单数量走向基本相同，因此可以判断，季节因素对于旅客取消订单的影响较小。

第二，根据酒店各月份的收入和订单数绘制棒棒糖图。结果显示，两图不仅呈现趋势相同，且变化程度也非常类似，这说明降价促销或者急剧涨价的情况并不明显，高订单量同时也带来了高收入。而对于各月份老客户的订单统计，并未从中发现明显规律。2015年10月的回头客订单最多，为125条记录，其次是2017年5月，为103条记录。

第三，对入住人数的统计。对订单的入住人员结构进行分析，可以发现，各月份的订单主体都是以成人为主，儿童和婴儿的比例极低。在大多数月份，几乎看不到婴儿的占比情况，这是符合我们的常理的。

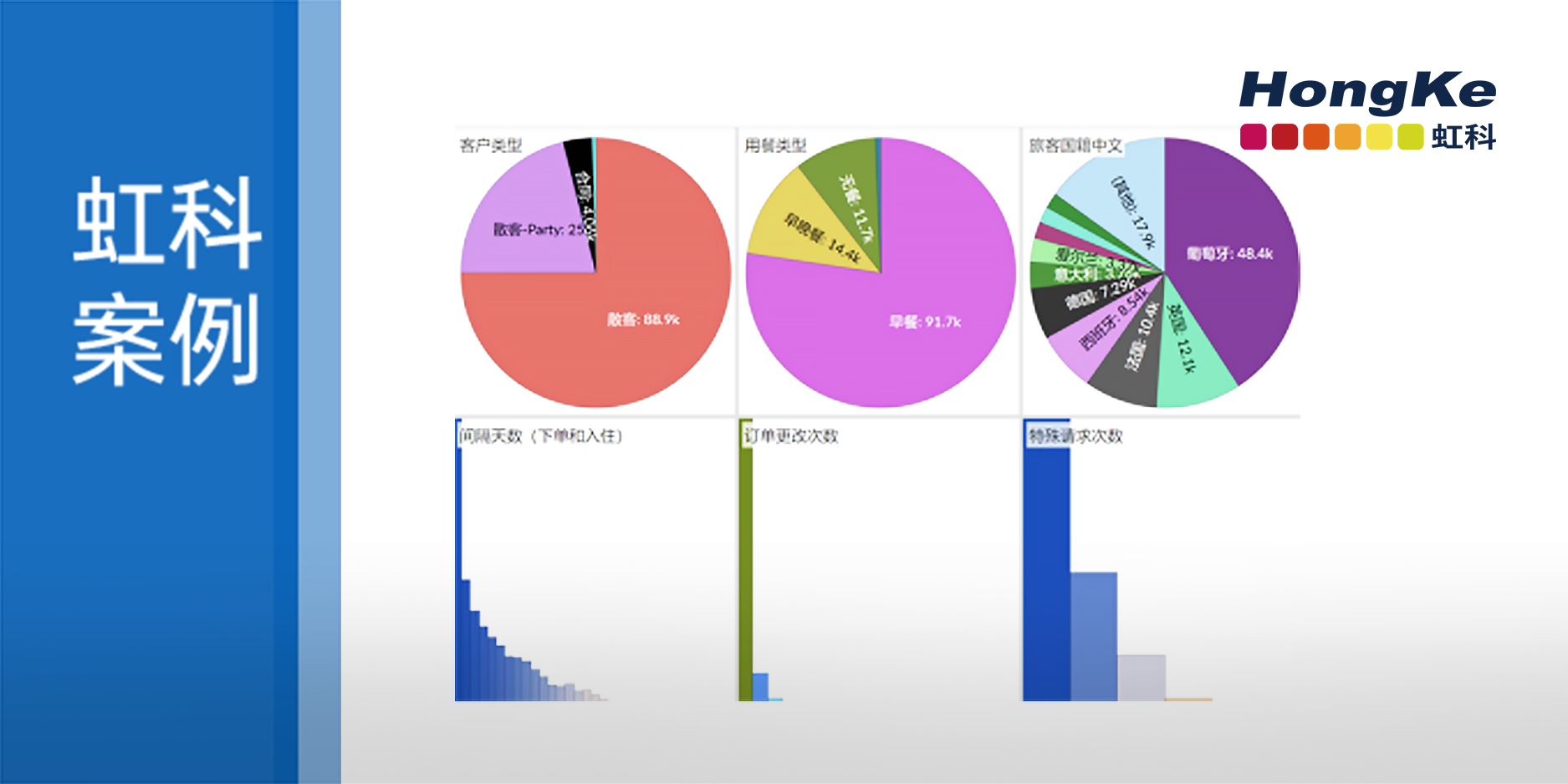
第四，对于旅客国籍分布，绘制树状图进行分析。其中来自葡萄牙、法国和德国的旅客最多，占比分别达到了39%、11%和8%。对于停车位的需求，图中显示，98%的旅客不需要停车位，2%的旅客只需要1个停车位，停车位需求数大于1的订单记录数仅为5条，几乎可以忽略不记，因此记为占比为0%。

第五，对于餐型的需求。绝大部分旅客只预订了早餐，占比第二高的是无餐，即不需要预订任何餐型，三餐都需要预订的订单占比是最小的。

3.取消预订分析

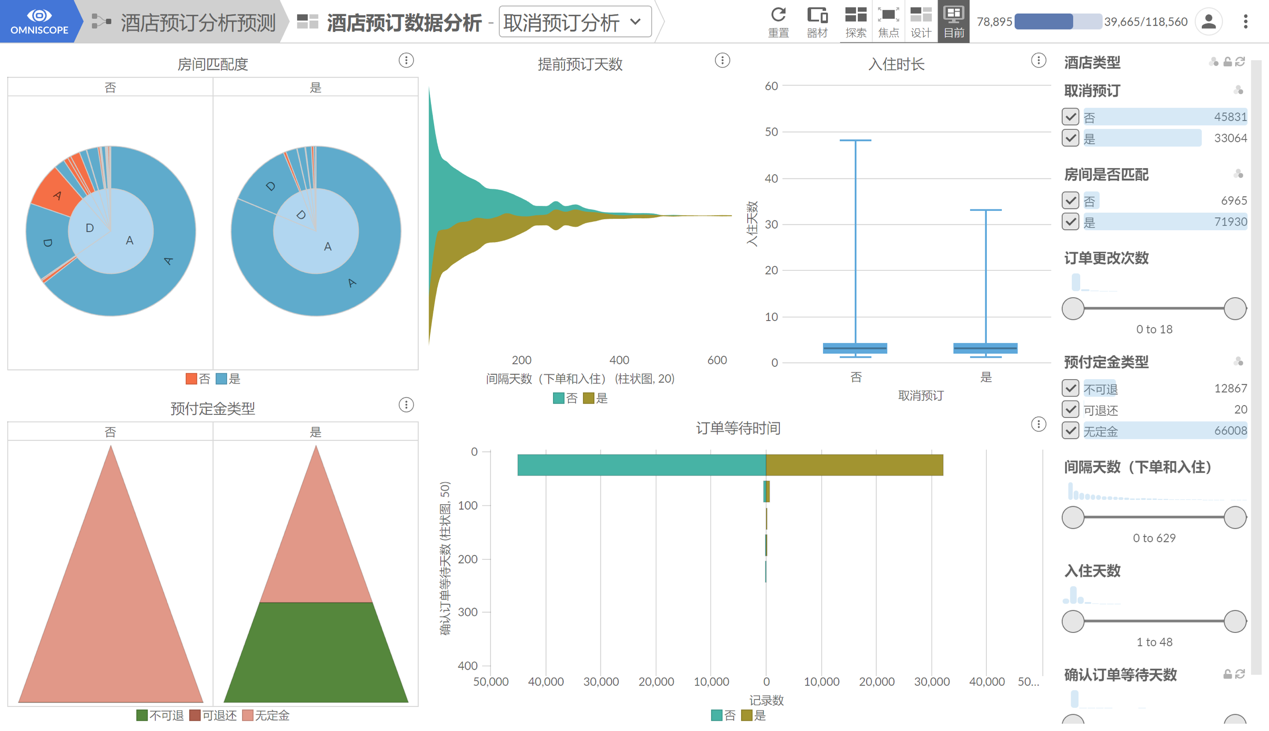
通过上述分析可以了解到，城市酒店的订单取消率达到了42%，这个数据不太理想。为提高酒店的盈利，对订单取消原因进行分析十分必要，从而可以有针对性的优化酒店运营，降低订单取消率。对此，我们找出5个可能导致旅客取消订单的因素，绘制了下面的仪表板：

编辑搜图

请点击输入图片描述（最多18字）

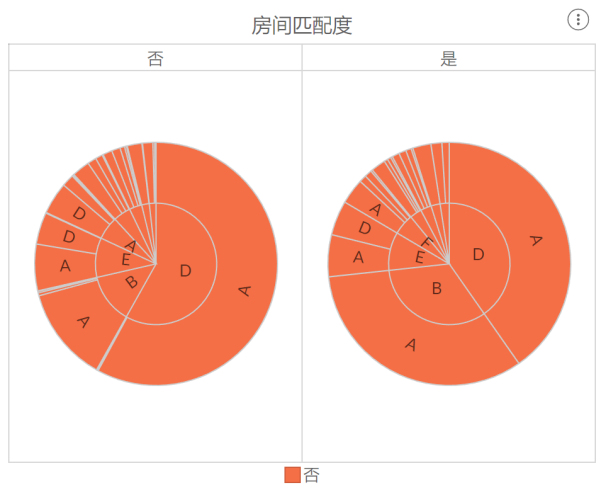
（1）房间匹配度

在78895条城市酒店数据中，有6965个订单的房间与旅客最初预订的房间不同，占比达到了8.83%。将这些房间匹配度为否的数据筛选出来，可以发现未取消订单和取消订单的二级饼图分布情况产生明显变化。

当旅客指定房间类型与最终预留房间类型为B-A或F-A时，更容易导致旅客取消订单。因此酒店在面临房源不足需要为旅客更改房间类型时，应该尽量避免这两种更改方案，以减少旅客订单取消率。

编辑搜图

请点击输入图片描述（最多18字）

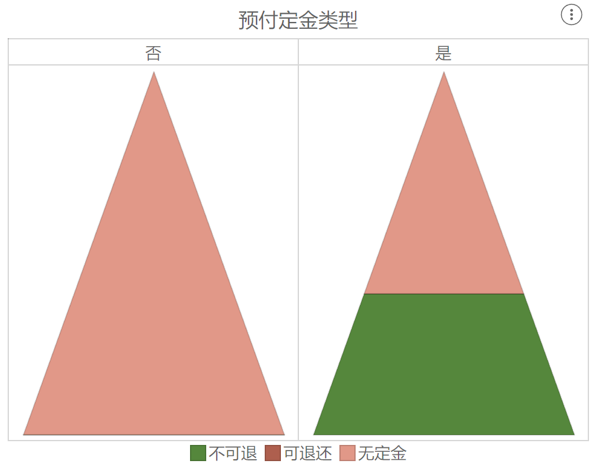
（2）预付定金类型

在所有城市酒店中，定金类型共有三种：不可退、可退还和无定金。据此可以分别绘制未取消订单和取消订单的金字塔图，从中发现未取消的订单几乎都属于无定金类型。而在所有的取消订单中，有12843条订单定金显示为不可退，占取消订单原因的比例高达38.86%。

据此可知，原本酒店设置定金不可退就是为了防止旅客取消订单，但很明显，这个操作并没有得到很好的防范效果，反而还很可能导致不良的口碑，因此酒店后期在设置定金规则时需更加谨慎。

编辑搜图

请点击输入图片描述（最多18字）

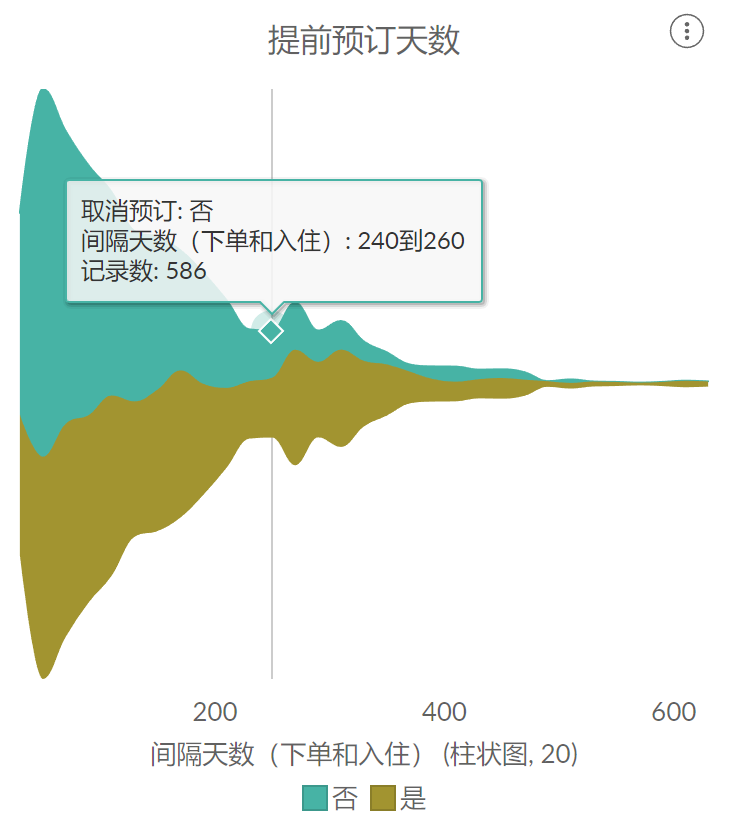
（3）提前预订天数

在所有城市酒店数据中，下单和入住间隔天数字段值的范围为0-629。绘制提前预订天数统计流图，发现不论订单是否取消，提前1个月预订的占比都是较高的。因为时间越长，旅客行程变化的可能性越大，也就更可能取消订单，所以为判断提前预订天数对取消订单的影响，可以将数据范围缩小到30以上，即30-629。

结果显示，当在提前240天以上预订订单时，旅客取消订单的可能性会大于不取消订单。因此酒店在计划开放提前预约服务时，可以考虑适当的缩短预约周期。

编辑搜图

请点击输入图片描述（最多18字）

（4）入住时长分析

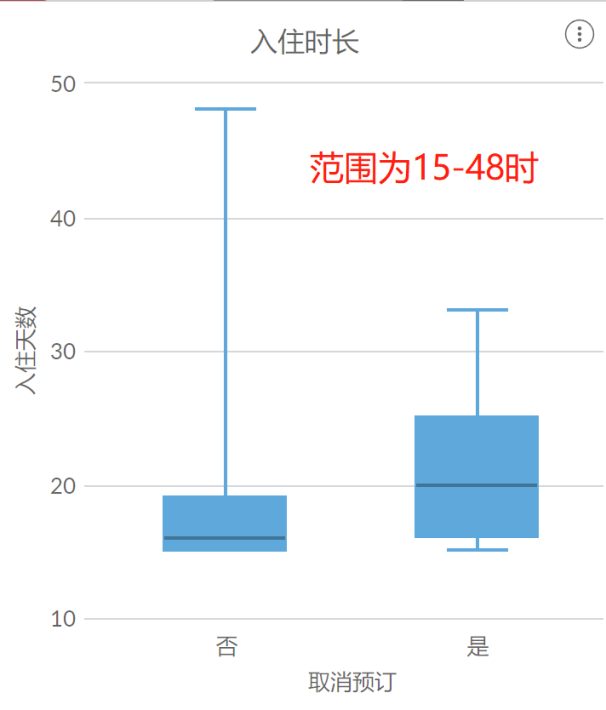
从上文我们已经知道，旅客预订的入住天数普遍在1-4天。以是否取消订单为类别，绘制两者的箱线图，发现两者中位数均为3，上四分位数均为4。

为了更好的分析入住时长对旅客取消订单的影响，将入住时长大于4天的数据筛选出来。结果发现，订单的取消率由最初的41.9%下降到40.71%，似乎入住时长对取消订单的影响并不大。然而，当我们把入住时长范围缩短到5-48天时，取消率达到了45.48%。当缩短到10-48天时，取消率达到了64.65%。当缩短到15-48时，取消率甚至到了76.97%。

这说明，入住时长在一定程度上确实是影响了订单的取消，这也可能和旅客个人的时间安排有关。酒店在这方面的优化措施可以是对大额订单给予一些优惠，以吸引旅客预订。

编辑搜图

请点击输入图片描述（最多18字）

（5）订单等待时间

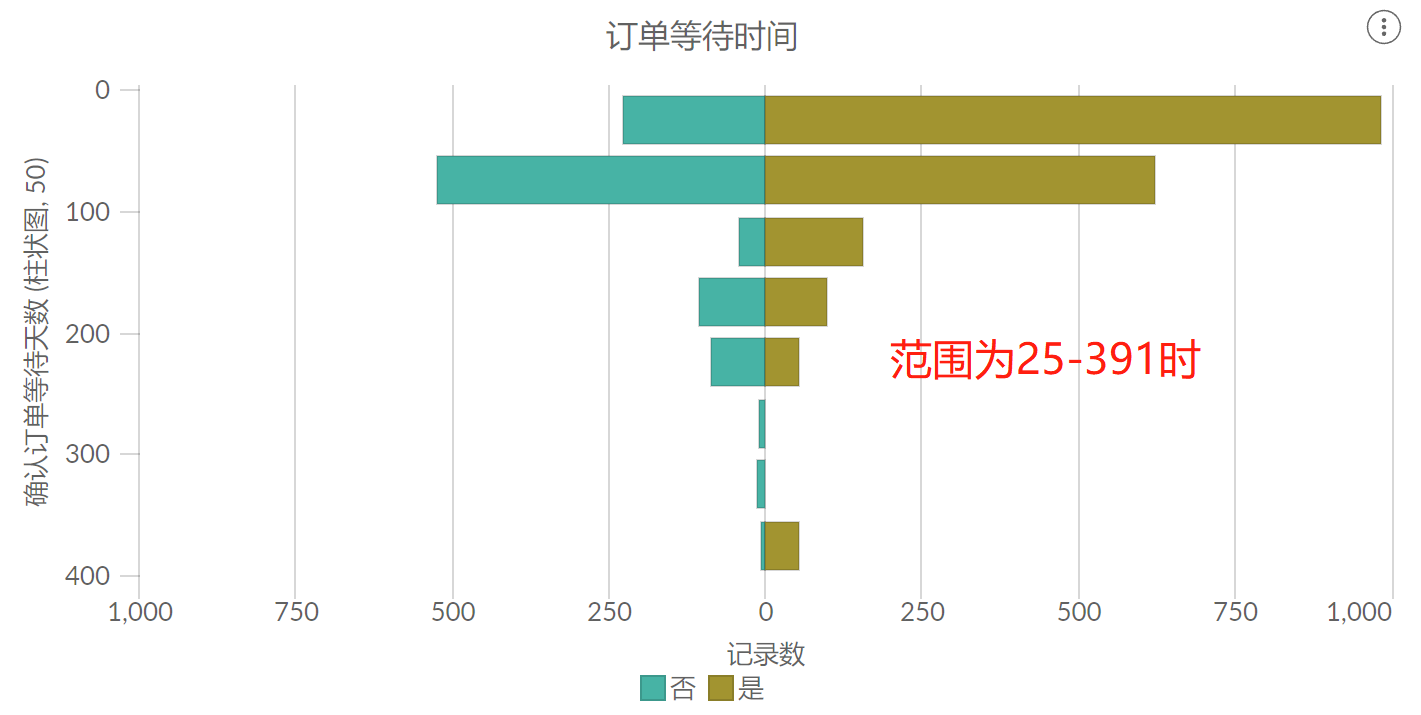
对于订单等待时间，即酒店确认订单的响应时间，值范围为0-391。不论订单最终是否取消，两个类别中0-25的响应时间占比都是最高的。

将数据范围缩短到25-391，发现数据的分布情况发生了非常大的变化。几乎各个区间，订单的取消量都超过了未取消的订单数，总体的订单取消率高达66%。如果将数据范围缩短到365-391，即订单等待时间超过1年时，订单取消率达到了96.7%。

这说明，酒店对客户的响应时间将在很大程度上决定订单是否成交。因此，酒店应优化内部的软硬件设施和员工培训，尽可能的缩短客户的等待时间。

编辑搜图

请点击输入图片描述（最多18字）

“关于虹科Visokio Omniscope你了解多少？”

请听题：

1. 虹科Visokio Omniscope支持哪些浏览器？(多选）

A.谷歌           B.Edge          C. Internet Explore          D.Safari            E.Firefox

2. 虹科Visokio Omniscope是否支持私有化部署？

是【】           否【】

记得点赞收藏转发，关注我们哦~不要错过下一期文末正确答案揭晓！当然，也欢迎评论区告诉我们你的观点，或者前往虹科云科技官网提前查看答案以及了解更多虹科Visokio相关资讯...

虹科提供的Visokio 是一套集ETL、分析、可视化、数据管理员、数据科学家、数据分析师等多重功能身份为一体的完美工具，是具备十足兼容性，开放性、可扩展性、协作性、自动化、和安全性于一身的自助式商业智能平台。

虹科是Visokio的中国区战略合作伙伴，虹科持续关注各行业当下急切需求，专注于为企业解答疑问，制定专属服务，一站式解决问题！为企业的数据分析与决策提供定制化方案！是无数企业实现商业智能的最佳合作选择！