P1543 [POI2004] SZP 题解

P1543 [POI2004] SZP 题解

传送门。

题目简述

有 \(n\) 个人，每个人都会监视另一个人，要求选出尽可能多的同学，使得选出的每一名同学都必定会被监视到。且选出的同学不可再监视其他人。

思路简述

因为任意一个人只能被另一个人管，那么就想到，如果没人管的同学就不能被选（不被监视）。

若某个人有多个人监视，且监视他的有至少一个专门监视（监视他的那个人没人监视）则他不得不去。

那么再看看如果出现环咋办。

不如画个图理解。

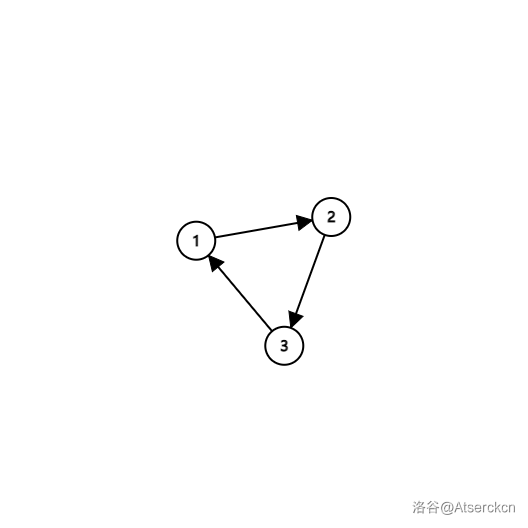
上图即为一个环：\(1\) 监视 \(2\)，\(2\) 监视 \(3\)，\(3\) 监视 \(1\)。

那么不妨枚举一下。

如果派出 \(1\)，则 \(3\) 可以监视到，而 \(2\) 也可以监视到 \(3\)，完美符合题意。

但是，若取出了 \(1\) 和 \(2\)，\(2\) 则会没人监视（本来监视他的 \(1\) 号走了）。

所以可以得出结论：若遇到环，设 \(s\) 为环的节点个数，则取出的个数为 \(\lfloor\frac{s}{2}\rfloor\)。

代码实现

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5;
int n,to[N],ans,cnt_ring,in[N];
bool gone[N]/*被选中了吗*/,vis_ring[N]/*遍历过了吗*/;
queue<int > q;//注意：这里的q可不是说进队列了就得被选中
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	{
		scanf("%d",&to[i]);
		++in[to[i]];//入度+1
	}
	for(int i=1;i<=n;i++)
		if(!in[i])//拓扑排序老板子
			q.push(i);
	while(!q.empty())
	{
		int t=q.front();q.pop();
		vis_ring[t]=true;//判断是否遍历过
		if(gone[t])//他走了，他监视的同学就看看情况
		{
			if((--in[to[t]])==0)
				q.push(to[t]);
		}
		else//他没走，他监视的孩子可就遭老罪喽
		{
			if(!gone[to[t]])//孩子没走
			{
				++ans;
				gone[to[t]]=true;//给我走
				q.push(to[t]);
			}
		}
	}
	for(int i=1;i<=n;i++)//开始判环
	{
		if(!vis_ring[i]&&in[i])
		{
			cnt_ring=0;//作用如其名
			for(int j=i;!vis_ring[j];j=to[j])
			{
				++cnt_ring;
				vis_ring[j]=true;
			}
			ans+=cnt_ring/2;//刚说的，不过C++自动向下取整
		}
	}
	printf("%d\n",ans);
	return 0;
}