多层感知机及其BP算法（Multi-Layer Perception）

Deep Learning 近年来在各个领域都取得了 state-of-the-art 的效果，对于原始未加工且单独不可解释的特征尤为有效，传统的方法依赖手工选取特征，而 Neural Network 可以进行学习，通过层次结构学习到更利于任务的特征。得益于近年来互联网充足的数据，计算机硬件的发展以及大规模并行化的普及。本文主要简单回顾一下 MLP ，也即为Full-connection Neural Network ，网络结构如下，分为输入，隐层与输出层，除了输入层外，其余的每层激活函数均采用 $sigmod$ ，MLP 容易受到局部极小值与梯度弥散的困扰，如下图所示：

MLP 的 Forward Pass

MLP 的 BP 算法基于经典的链式求导法则，首先看前向传导，对于输入层有 $I$ 个单元， 对于输入样本 $(x,z)$ ，隐层的输入为：

\[a_h = \sum_{i=1}^I w_{ih}x_i\]

\[b_h = f(a_h)\]

这里函数 $f$  为 非线性激活函数，常见的有$sigmod$ 或者是 $tanh$，本文选取 $sigmod$ 作为激活函数。计算完输入层向第一个隐层的传导后，剩下的隐层计算方式类似，用 $h_l$ 表示第 $l$ 层的单元数：

\[a_h = \sum_{h'=1}^{h_{l-1}}w_{h'h}b_{h'}\]

\[b_h = f(a_h)\]

对于输出层，若采用二分类即 $logistic  \ regression$ ，则前向传导到输出层：

\[a = \sum_{h'}w_{h'h}b_{h'}\]

\[y = f(a)\]

这里   $y$ 即为 MLP 的输出类别为 1 的概率，输出类别为 0 的概率为 $1-y$，为了训练网络，当 $z=1$ 时，$y$ 越大越好，而当 $z=0$ 时， $1-y$越大越好 ，这样才能得到最优的参数 $w$ ，采用 MLE 的方法，写到一起可以得到 $y^z(1-y)^{1-z}$ ,这便是单个样本的似然函数，对于所有样本可以列出 $log$ 似然函数  $O = \sum_{(x,z)} zlogy + (1-z)log(1-y) $ ，直接极大化该似然函数即可，等价于极小化以下的 $-log$ 损失函数：

\[O = - \left [ \sum_{(x,z)}  zlogy + (1-z)log(1-y)  \right ] \]

对于多分类问题，即输出层采用   $softmax$ ，假设有 $K$ 个类别，则输出层的第 $k$ 个单元计算过程如下:

\[a_k =\sum_{h'} w_{h'k}b_{h'} \]

\[y_k = f(a_k)\]

则得到类别 k 的概率可以写作 $ \prod_ky_k^{z_k}$ ，注意标签 $z$ 中只有第 $k$ 维为 1，其余为 0，所以现在只需极大化该似然函数即可:

\[O =\prod_{(x,z)} \prod_{k}y_k^{z_k}\]

同理等价于极小化以下损失：

\[ O = -\prod_{(x,z)} \prod_{k}y_k^{z_k}\]

以上便是 $softmax$ 的损失函数，这里需要注意的是以上优化目标 $O$ 均没带正则项，而且 $logistic$ 与 $softmax$ 最后得到的损失函数均可以称作交叉熵损失，注意和平方损失的区别。

Backward Pass

有了以上前向传导的过程，接下来看误差的反向传递，对于 $sigmod$ 来说，最后一层的计算如下：$a =\sum_h w_h \cdot b_h$ ，$y = f(a) = \sigma(a) $ ，这里 $b_h$ 为倒数第二层单元 $h$ 的输出，$\sigma$  为 $sigmod$ 激活函数，且满足  $\sigma '(a) = \sigma(a) (1-\sigma(a))$ ，对于单个样本的损失 ：

\[O = -\left [z log(\sigma(a) +(1-z)log(1-\sigma(a))  \right ]\]

可得到如下的链式求导过程：

\[\frac{\partial O}{\partial w_h} =   \frac{\partial O}{\partial a} \cdot \frac{\partial a}{\partial w_h}\]

显而易见对于后半部分 $\frac{\partial a}{\partial w_h}$ 为  $b_h$ ，对于前半部分 $\frac{\partial O}{\partial a} $ ：

\begin{aligned}
\frac{\partial O}{\partial a}
&=-\frac{\partial \left [z \ log(\sigma(a)) +(1-z)log(1-\sigma(a)) \right ] }{\partial a}\\
&=-\left [ \frac{z}{\sigma(a)} - \frac{1 - z}{1 - \sigma(a)} \right ]\sigma'(a) \\
&=-\left [ \frac{z}{\sigma(a)} - \frac{1 - z}{1 - \sigma(a)} \right ]\sigma(a)(1-\sigma(a))\\
&= \sigma(a) -z\\
&= y - z
\end{aligned}

以上，便得到了 $logistic$ 的残差，接下来残差反向传递即可，残差传递形式同 $softmax$ ，所以先推倒 $softmax$ 的残差项，对于单个样本， $softmax$ 的 $log$ 损失函数为：

\[O = -\sum_iz_i logy_i\]

其中：

\[y_i = \frac{e^{a_i}}{\sum_je^{a_j}}\]

根据以上分析，可以得到 $y_{k'}$ 关于 $a_k$ 的导数:

\[\frac{\partial y_{k'}}{\partial a_k}=\left\{
\begin{aligned}
\frac{\sum_{i \ne k}e^{a_j} \cdot e^{a_k}}{\sum_je^{a_j} \cdot \sum_je^{a_j} } &=y_k (1-y_k)\ \ \ \ k'=k\\
\frac{e^{a_{k'}} \cdot e^{a_k}}{\sum_je^{a_j} \cdot \sum_je^{a_j} } &=-y_{k'}y_k \ \ \ \ \ \ \ \ \ k \neq k
\end{aligned}
\right.\]

现在能得到损失函数 $O$ 对于 $a_k$ 的导数：

\[\begin{aligned}
\frac{\partial O}{\partial a_k} &= \frac{\partial\left [ -\sum_iz_ilogy_i \right ]}{\partial a_k} \\
&= -\sum_iz_i \cdot \frac{\partial logy_i}{\partial a_k} \\
&= -\sum_iz_i \frac{1}{y_i} \frac{\partial y_i}{\partial a_k} \\
&= -z_k(1-y_k) - \sum_{i \ne k} z_i \frac{1}{y_i}(-y_i y_k) \\
&= -z_k + z_ky_k + \sum_{i \ne k} z_i y_k \\
&= -z_k + y_k(\sum_iz_i) \\
&=y_k-z_k
\end{aligned}\]

这里有  $\sum_iz_i = 1$ ，即只有一个类别。  到这一步， $softmax$ 与 $sigmod$  的残差均计算完成，可以用符号 $\delta$ 来表示，对于单元 $j$ ，其形式如下：

\[\delta_j = \frac{\partial O}{\partial a_j}\]

这里可以得到 $softmax$  层向倒数第二层的残差反向传递公式：

\[  \delta_h = \frac{\partial O}{\partial b_h} \cdot \frac{\partial b_h}{\partial a_h} = \frac{\partial b_h}{\partial a_h} \sum_{k}\frac{\partial O}{\partial a_k} \cdot \frac{\partial a_k}{\partial b_h} = f'(a_h) \sum_k w_{hk}\delta_k\]

其中 $ a_k = \sum_hw_{hk}b_h $ ，对于 $sigmod$ 层，向倒数第二层的反向传递公式为：

\[  \delta_h = \frac{\partial O}{\partial b_h} \cdot \frac{\partial b_h}{\partial a_h} = \frac{\partial b_h}{\partial a_h} \cdot \frac{\partial O}{\partial a} \cdot \frac{\partial a}{\partial b_h} = f'(a_h) w_h\delta\]

以上公式的 $\delta$ 代表 $sigmod$ 层唯一的残差，接下来就是残差从隐层向前传递的传递过程，一直传递到首个隐藏层即第二层（注意，残差不会传到输入层，因为不需要，对输入层到第二层的参数求导，其只依赖于第二层的残差，因为第二层是这些参数的放射函数）：

\[ \delta_h =   f'(a_h) \sum_{h'=1}^{h_{l+1}} w_{hh'}\delta_{h'}\]

整个过程可以看下图：

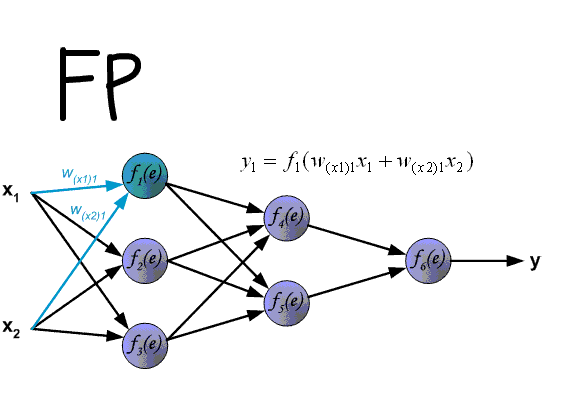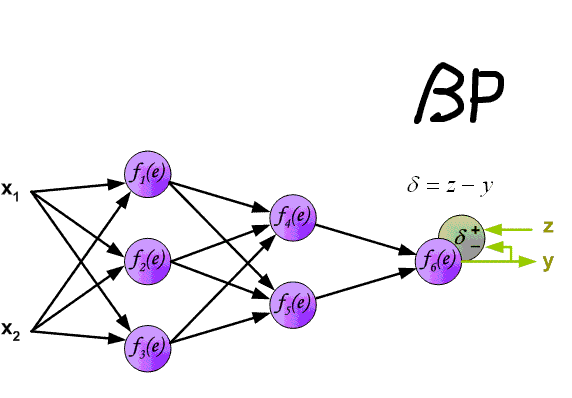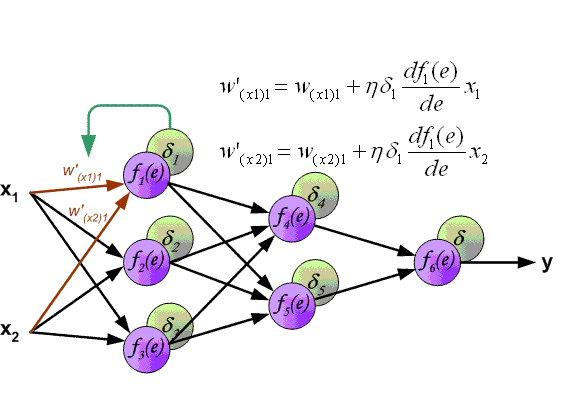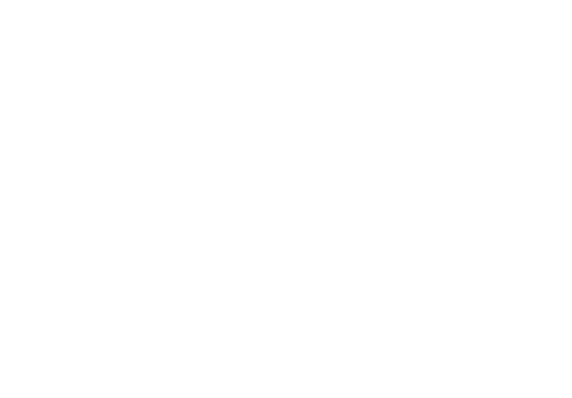
最终得到关于权重的计算公式：

\[\frac{\partial O}{\partial w_{ij}} = \frac{\partial O}{\partial a_{j}} \frac{\partial a_j}{\partial w_{ij}} = \delta_jb_i\]

至此完成了backwark pass 的过程，注意由于计算比较复杂，有必要进行梯度验证。对函数  $O$ 关于参数 $w_{ij}$ 进行数值求导即可，求导之后与与上边的公式验证差异，小于给定的阈值即认为我们的运算是正确的。