洛谷P3195||bzoj1010 [HNOI2008]玩具装箱TOY

洛谷P3195

bzoj1010

设s数组为C的前缀和

首先$ans_i=min_{j<i}\{ans_j+(i-j-1+s_i-s_j-L)^2\}$

（斜率优化dp）参考(复读)https://www.cnblogs.com/orzzz/p/7885971.html

设j不比k劣，则$ans_j+(i-j-1+s_i-s_j-L)^2 <= ans_k+(i-k-1+s_i-s_k-L)^2$

化简，与i相关的放到一边，（由于要除法，设$k+s_k-j-s_j>0$）

得$2(i+s_i)<=\frac{x_k-x_j+(k+s_k)^2-(j+s_j)^2+2(k+s_k)(L+1)-2(j+s_j)(L+1)}{k+s_k-j-s_j}$

设$f(k)=x_k+(k+s_k)^2+2(k+s_k)(L+1)$，$g(k)=k+s_k$，则$2(i+s_i)<=\frac{f(k)-f(j)}{g(k)-g(j)}$

也就是说，当$g(k)>g(j)$时，当且仅当满足这个条件时，j不比k劣

对于每个j，都表示为二维平面上一个点$(g(j),f(j))$

如果有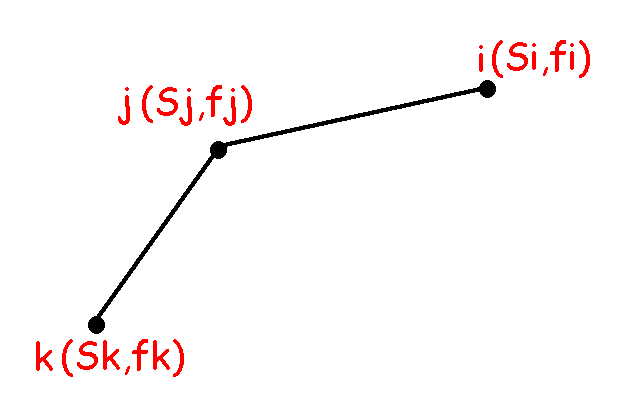这样三个点i,j,k（图中横坐标分别改成g(i),g(j),g(k)），

那么$\frac{f(i)-f(j)}{g(i)-g(j)}<\frac{f(j)-f(k)}{g(j)-g(k)}$

可以发现，不管$2(i+s_i)$会插入到与这两者有关的什么位置（比两者都小，夹在中间，比两者都大），j都不可能是最优解

因此，只有下凸壳上面的点才可能是最优解，可以在算出i的答案并加入i的同时维护一下下凸壳（此处$g(i)=i+s_i$是单调的，直接栈维护即可）

怎么样在下凸壳找到这个最优解呢？

考虑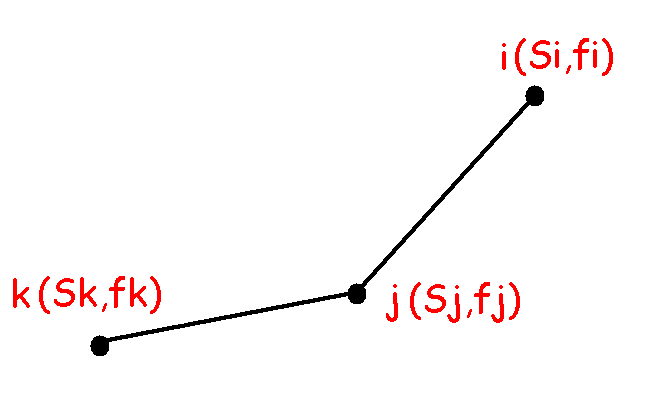这样三个点i,j,k（图中横坐标分别改成g(i),g(j),g(k)），

那么$\frac{f(i)-f(j)}{g(i)-g(j)}>\frac{f(j)-f(k)}{g(j)-g(k)}$

可以发现，如果$2(i+s_i)$比两者都大，那么i最优；如果夹在中间，则j最优；如果比两者都小，则k最优

把3个点扩展到很多个点，可以发现如果搞出一个线段集合，表示下凸壳相邻两点间连线的集合，在这个集合中取出一条斜率>$2(i+s_i)$并且最小的线段，这条线段靠前(靠左)的那个点就是最优解（意会一下）（下凸壳边界点可能要特判）

由于此处$2(i+s_i)$是单调的，可以用一个指针直接维护这个最优解的位置

 #include<cstdio>
 #include<algorithm>
 #include<cstring>
 #include<vector>
 using namespace std;
 #define fi first
 #define se second
 #define mp make_pair
 #define pb push_back
 typedef long long ll;
 typedef unsigned long long ull;
 struct P
 {
     ll x,y,n;
 };
 P operator-(const P &a,const P &b)
 {
     return (P){a.x-b.x,a.y-b.y,};
 }
 ll cross(const P &a,const P &b)
 {
     return a.x*b.y-b.x*a.y;
 }
 inline ll sqr(ll x){return x*x;}
 P tmp[];int l,r;
 int n;ll L;
 ll s[],ans[];
 int main()
 {
     int i;ll t1;P tn;
     scanf("%d%lld",&n,&L);
     for(i=;i<=n;++i)
     {
         scanf("%lld",s+i);
         s[i]+=s[i-];
     }
     l=;r=;
     tmp[++r]=(P){,,};
     for(i=;i<=n;++i)
     {
         t1=*(i+s[i]);
         while(l<r && tmp[l+].y-tmp[l].y <= t1*(tmp[l+].x-tmp[l].x))    ++l;
         if(l>r)    l=r;
         ans[i]=ans[tmp[l].n]+sqr(i-tmp[l].n-+s[i]-s[tmp[l].n]-L);
         tn=(P){i+s[i],ans[i]+(i+s[i])*(i+s[i]+*L+),i};
         while(r>= && cross(tn-tmp[r-],tmp[r]-tmp[r-])>=)    --r;
         tmp[++r]=tn;
     }
     printf("%lld\n",ans[n]);
     return ;
 }

---

为什么是凸包呢？好像还有一种解释方法

化简一下$ans_j+(i-j-1+s_i-s_j-L)^2$=$(i+s_i)^2-2(i+s_i)(j+s_j+L+1)+(j+s_j+L+1)^2+x_j$

其中$(i+s_i)^2$只与i有关，先提出去，

剩下$-2(i+s_i)(j+s_j+L+1)+(j+s_j+L+1)^2+x_j$

设其为z，现在要求z的最小值

发现这个过程类似线性规划，等式为$z=-2(i+s_i)(j+s_j+L+1)+(j+s_j+L+1)^2+x_j$

即$(j+s_j+L+1)^2+x_j=2(i+s_i)(j+s_j+L+1)+z$

设$x=j+s_j+L+1$，$y=(j+s_j+L+1)^2+x_j$，$a=2(i+s_i)$，则$y=ax+z$

对于每个j<i，可以看做平面上一个点(x,y)，得到点集S

现在有直线$y=ax+z$，a是定值，z不确定，要使得它经过S中一个点，且截距z最小，就拿这条直线从右往左移，碰到第一个点时停下来

显然，只有点集的下凸壳上的点有可能被靠到（也有可能靠到下凸壳的一条边上，这时边的两个端点都是最优解）

下凸壳的性质是：形成它的各条线段的斜率递增

因此，要找到这条直线会靠到什么地方，维护下凸壳，在上面按斜率二分一下就行（这题有特殊性质，也可以用一个指针维护）

话说推出来的式子跟上面不一样，但是仍然可以A？

 #include<cstdio>
 #include<algorithm>
 #include<cstring>
 #include<vector>
 using namespace std;
 #define fi first
 #define se second
 #define mp make_pair
 #define pb push_back
 typedef long long ll;
 typedef unsigned long long ull;
 struct P
 {
     ll x,y,n;
 };
 P operator-(const P &a,const P &b)
 {
     return (P){a.x-b.x,a.y-b.y,};
 }
 ll cross(const P &a,const P &b)
 {
     return a.x*b.y-b.x*a.y;
 }
 inline ll sqr(ll x){return x*x;}
 P tmp[];int l,r;
 int n;ll L;
 ll s[],ans[];
 int main()
 {
     int i;ll t1;P tn;
     scanf("%d%lld",&n,&L);
     for(i=;i<=n;++i)
     {
         scanf("%lld",s+i);
         s[i]+=s[i-];
     }
     l=;r=;
     tmp[++r]=(P){L+,sqr(L+),};
     for(i=;i<=n;++i)
     {
         t1=*(i+s[i]);
         while(l<r && tmp[l+].y-tmp[l].y <= t1*(tmp[l+].x-tmp[l].x))    ++l;
         if(l>r)    l=r;
         ans[i]=ans[tmp[l].n]+sqr(i-tmp[l].n-+s[i]-s[tmp[l].n]-L);
         tn=(P){i+s[i]+L+,ans[i]+sqr(i+s[i]+L+),i};
         while(r>= && cross(tn-tmp[r-],tmp[r]-tmp[r-])>=)    --r;
         tmp[++r]=tn;
     }
     printf("%lld\n",ans[n]);
     return ;
 }

---

其他资料（未看，咕咕咕）

https://www.cnblogs.com/MashiroSky/p/6009685.html

https://blog.csdn.net/lxc779760807/article/details/51366552

https://codeforces.com/blog/entry/63823

https://www.cnblogs.com/flashhu/p/9480669.html