机器学习 Support Vector Machines 1

引言

这一讲及接下来的几讲，我们要介绍supervised learning 算法中最好的算法之一：Support Vector Machines (SVM,支持向量机)。为了介绍支持向量机，我们先讨论“边界”的概念，接下来，我们将讨论优化的边界分类器，并将引出拉格朗日数乘法。我们还会给出 kernel function 的概念，利用 kernel function，可以有效地处理高维(甚至无限维数)的特征向量，最后，我们会介绍SMO算法，该算法说明了如何高效地实现SVM。

Margin 边界

我们的SVM之旅，从边界的讨论开始，我们要讨论边界的概念以及预测的置信度等概念。

考虑 logistic regression， 其概率 p(y=1|x;θ) 由函数 hθ(x)=g(θTx) 估计，我们预测一个输入向量的输出为 “1” 当且仅当其概率 hθ(x)⩾0.5,或者 θTx⩾0, 考虑一个正样本(y=1)。如果 θTx 越大，意味着其概率 hθ(x)=p(y=1|x;w,b) 也越大，因此我们有更高的置信度将该样本判定为正样本(y=1)。一般情况下，当 θTx≫0, 我们非常确信该样本的输出为 1, 同样地，当 θTx≪0，我们非常确信该样本为负样本，y=0。给定一组训练样本，我们希望可以找到这样一组参数 θ，使得对于任何的正样本 y(i)=1，满足 θTx(i)≫0；而对于任何的负样本y(i)=0, 满足θTx(i)≪0，如果能找到这样一组参数，那对于分类器来说，它可以有很高的置信度区分正负样本，这是分类问题的非常理想的结果。我们将在后面用 function margin (函数边界)的概念描述这个想法。

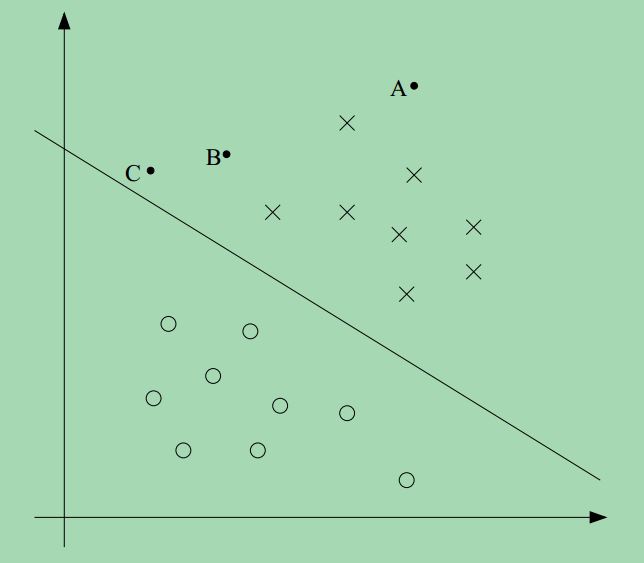
我们先来考虑如下一张图，其中 × 表示正样本，∘ 表示负样本。决策边界 (在图中就是那条直线，由 θTx=0 定义，这条线也称为分界面。图上三个点分别标为：A,B,C.

我们注意到点A离决策边界非常远，如果要我们判断点A，我们有很高的置信度判断点A为正样本，其y=1。但是对于点C，我们发现它离决策边界很近，在图上所示的情况下，我们知道点C是正样本，我们预测其输出y=1，但是我们也注意到，如果决策边界稍微有点改变，则点C有可能被判断为负样本，预测的输出为y=0。因此，从图上各点的分布以及决策边界的位置，我们可以说我们对于点A的预测比对点C的预测更加自信，换句话说，点A的置信度比点C高。我们看到，如果一个点离决策边界越远，那么分类器判断的时候置信度也会更高。因此，给定一组训练样本，我们试着找到这样一个决策边界，使得分类器对所有训练样本的判断都有一个很高的置信度(意味着所有的点都要尽可能地远离决策边界)，我们稍后将用 geometric margin (几何边界)的概念去实现这个想法。

在介绍函数边界和几何边界之前，我们要先定义一些符号。我们考虑用线性分类器解决二分类问题，其输出为y，输入的特征向量为x，现在我们要用{−1,1}而不是{0,1}来表示样本的输出。我们不再用向量θ来表示我们需要求的参数，现在换成了参数w,b，而线性分类器的表达式为：

hw,b(x)=g(wTx+b)

其中，函数g满足，g(z)=1 当 z>0，反之 g(z)=−1当，z<0。w 还是一个向量，而b相当于截距。

从分类器的函数表达式可以看出，我们将直接预测样本的输出为1或者-1，而不再像logistic regression那样，先判断其概率，然后再判断样本的输出。

函数边界和几何边界

接下来，我们探讨函数边界和几何边界，给定一组训练样本(x(i),y(i))，我们定义某个样本的函数边界为：

γ^(i)=y(i)(wTx+b)

如果y(i)=1，那么为了使得函数边界尽可能地大，我们需要wTx+b是一个很大的正数，相反得，如果y(i)=−1，我们希望wTx+b是一个绝对值很大的负数。

进一步的，如果 y(i)(wTx+b)>0，那么我们的预测就是对的(这个应该很容易验证)。因此，一个大的函数边界意味着一个可靠的，正确的预测。

对于线性分类器，其函数为g，我们发现如果函数g的参数w，b变成2w，2b，由于g(wTx+b)=g(2wTx+2b)，因此hw,b(x)不会有任何改变，因为hw,b(x) 取决于 wTx+b的符号而不是大小。虽然如此，但是(w,b)变成(2w,2b)还是使得函数边界乘以了2. 从中可以看出，我们可以通过任意改变w,b的尺度，使得函数边界取任意的值而不会使hw,b(x)有任何变化。直观上，我们可以引入如下的归一化，即∥w∥2=1，我们可以将w,b替换成(w/∥w∥2,b/∥w∥2)，我们考虑参数(w/∥w∥2,b/∥w∥2) 所表示的函数边界。我们稍后将会回到这个问题。

给定一组训练样本，S={(x(i),y(i));i=1,2...m},我们定义参数w,b关于训练集S的函数边界为所有样本的函数边界的最小值，称为γ^,可以定义为：

γ^=mini=1,2,...mγ^(i)

因此，一个训练集的\textbf{函数边界}，就是该训练集中所有样本的函数边界的最小值。

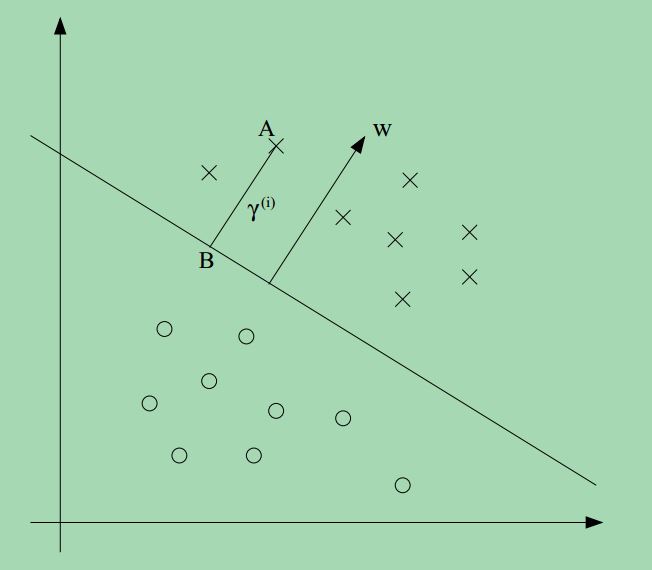
接下来，我们讨论几何边界，考虑如下的一张图：

w,b对应的决策边界已经给出，沿着w的方向，请注意，w是垂直于分界面的(这一点应该容易证明)。考虑点A，表示某个正样本，点A到决策边界的距离 γ(i)，由线段AB表示。

如何确定γ(i)的值?w/∥w∥是一个与w方向相同的单位长度的向量，点A表示特征向量x(i)，点B可以表示为：x(i)−γ(i)⋅w/∥w∥, 我们知道这点在决策边界上，所有在决策边界上的点满足wTx+b=0. 因此：

wT(x(i)−γ(i)w∥w∥)+b=0

进而可以求得γ(i)为：

γ(i)=wTx(i)+b∥w∥=(w∥w∥)Tx(i)+b∥w∥

上式给出的是正样本的情况，更一般地，我们定义一个样本关于参数w,b的几何边界为：

γ(i)=y(i)⎛⎝(w∥w∥)Tx(i)+b∥w∥⎞⎠

我们可以发现如果 ∥w∥=1，那么函数边界和几何边界相等，这个表达式提供了一种将两种边界联系起来的渠道。同样可以看到几何边界具有尺度不变性，如果将w,b 替换成2w,2b，可以看到几何边界不会改变。稍后我们将会看到，正是这种尺度不变性，让我们在拟合训练样本的时候，可以任意寻找参数w,b，而不会对函数性质产生多大的变化。

最后，我们给出几何边界的定义, 与函数边界的定义类似，给定一组训练样本，S={(x(i),y(i));i=1,2...m},我们定义参数w,b关于训练集S的几何边界为所有样本的几何边界的最小值，称为γ^,可以定义为：

γ=mini=1,2,...mγ(i)

因此，一个训练集的几何边界，就是该训练集中所有样本的几何边界的最小值。

参考文献

Andrew Ng, “Machine Learning”, Stanford University.