自顶向下归并排序（Merge Sort）

一、自顶向下的归并排序思路：

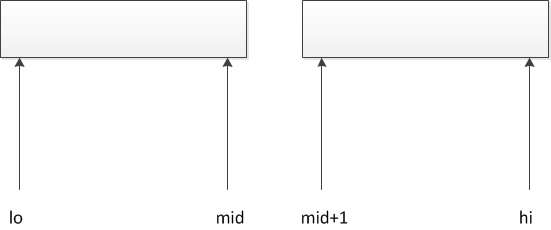
1、先把数组分为两个部分。

2、分别对这两个部分进行排序。

3、排序完之后，将这两个数组归并为一个有序的数组。

重复1-3步骤，直到数组的大小为1，则直接返回。

这个思路用递归函数来实现最方便，其中mid的计算公式：mid = lo + (hi-lo)/2，lo初始化为0，hi初始化为input.length - 1。

二、代码实现

package com.qiusongde;

import edu.princeton.cs.algs4.In;
import edu.princeton.cs.algs4.StdOut;

public class Merge {

    private static Comparable[] aux;

    public static void sort(Comparable[] input) {
        int N = input.length;
        aux = new Comparable[N];
        sort(input, 0, N-1);
    }

    private static void sort(Comparable[] input, int lo, int hi) {

        if(lo >= hi)//just one entry in array
            return;

        int mid = lo + (hi-lo)/2;
        sort(input, lo, mid);
        sort(input, mid+1, hi);
        merge(input, lo, mid, hi);

    }

    private static void merge(Comparable[] input, int lo, int mid, int hi) {

        //copy input[lo,hi] to aux[lo,hi]
        for(int i = lo; i <= hi; i++) {
            aux[i] = input[i];
        }

        int i = lo;
        int j = mid + 1;
        for(int k = lo; k <= hi; k++) {
            if(i > mid)
                input[k] = aux[j++];
            else if(j > hi)
                input[k] = aux[i++];
            else if(less(aux[j], aux[i]))
                input[k] = aux[j++];
            else
                input[k] = aux[i++];
        }

        StdOut.printf("merge(input, %4d, %4d, %4d)", lo, mid, hi);
        show(input);//for test

    }

    private static boolean less(Comparable v, Comparable w) {

        return v.compareTo(w) < 0;

    }

    private static void show(Comparable[] a) {

        //print the array, on a single line.
        for(int i = 0; i < a.length; i++) {
            StdOut.print(a[i] + " ");
        }
        StdOut.println();

    }

    public static boolean isSorted(Comparable[] a) {

        for(int i = 1; i < a.length; i++) {
            if(less(a[i], a[i-1]))
                return false;
        }

        return true;

    }

    public static void main(String[] args) {

        //Read strings from standard input, sort them, and print.
        String[] input = In.readStrings();
        show(input);
        sort(input);
        assert isSorted(input);
        show(input);

    }

}

测试数据：M E R G E S O R T E X A M P L E

输出结果：

M E R G E S O R T E X A M P L E
merge(input,    0,    0,    1)E M R G E S O R T E X A M P L E
merge(input,    2,    2,    3)E M G R E S O R T E X A M P L E
merge(input,    0,    1,    3)E G M R E S O R T E X A M P L E
merge(input,    4,    4,    5)E G M R E S O R T E X A M P L E
merge(input,    6,    6,    7)E G M R E S O R T E X A M P L E
merge(input,    4,    5,    7)E G M R E O R S T E X A M P L E
merge(input,    0,    3,    7)E E G M O R R S T E X A M P L E
merge(input,    8,    8,    9)E E G M O R R S E T X A M P L E
merge(input,   10,   10,   11)E E G M O R R S E T A X M P L E
merge(input,    8,    9,   11)E E G M O R R S A E T X M P L E
merge(input,   12,   12,   13)E E G M O R R S A E T X M P L E
merge(input,   14,   14,   15)E E G M O R R S A E T X M P E L
merge(input,   12,   13,   15)E E G M O R R S A E T X E L M P
merge(input,    8,   11,   15)E E G M O R R S A E E L M P T X
merge(input,    0,    7,   15)A E E E E G L M M O P R R S T X
A E E E E G L M M O P R R S T X 

三、性能分析

结论1：对于长度为N的任意数组，自顶向下归并排序需要1/2NlgN至NlgN次比较（less(aux[j], aux[i])）。

分析：见P272

结论2：对于长度为N的任意数组，自顶向下归并排序所需要的数组访问最大次数为6NlgN。

分析：每调用merge函数一次，2N次数组访问用于复制，2N次用于将排好序的元素移动回去，还有最多2N次用于比较。

四、算法改进

1、切换为插入排序

对于小数组来说，快速排序比插入排序慢。

2、测试数组是否已经有序

添加一个判断条件，如果a[mid]小于等于a[mid+1]，我们就认为数组是有序的了，并跳过merge函数。

    private static void sort(Comparable[] input, int lo, int hi) {

        if(lo >= hi)//just one entry in array
            return;

        int mid = lo + (hi-lo)/2;
        sort(input, lo, mid);
        sort(input, mid+1, hi);

        if(!less(input[mid+1],input[mid]))//input[mid+1] >= input[mid]
            return;

        merge(input, lo, mid, hi);

    }

3、不将元素复制到辅助数组

这种方法需要在递归调用的每个层次交换输入数组和辅助数组的角色。

　　public static void sort(Comparable[] input) {
        int N = input.length;
        aux = input.clone();//must be clone(the same as input)
//        StdOut.println("input:" + input + " aux:" + aux);//for test
        sort(aux, input, 0, N-1);
    }

    //this level takes source as input(need to be sorted)
    //and destination as auxiliary, and put the result in destination
    private static void sort(Comparable[] source, Comparable[] destination, int lo, int hi) {//avoid copy

        if(lo >= hi)//just one entry in array
            return;

        int mid = lo + (hi-lo)/2;
        sort(destination, source, lo, mid);//down level switch the roles of the input array and auxiliary array
        sort(destination, source, mid+1, hi);
        merge(source, destination, lo, mid, hi);//merge sorted source to destination

    }

    private static void merge(Comparable[] source, Comparable[] destination, int lo, int mid, int hi) {

        int i = lo;
        int j = mid + 1;
        for(int k = lo; k <= hi; k++) {
            if(i > mid)
                destination[k] = source[j++];
            else if(j > hi)
                destination[k] = source[i++];
            else if(less(source[j], source[i]))
                destination[k] = source[j++];
            else
                destination[k] = source[i++];
        }
//        StdOut.println("source:" + source + " destination:" + destination);//for test
//        StdOut.printf("merge(source, destination, %4d, %4d, %4d)", lo, mid, hi);//for test
//        show(destination);//for test

    }