51nod 1781 Pinball（线段树）

题面

Pinball的游戏界面由m+2行、n列组成。第一行在顶端。一个球会从第一行的某一列出发，开始垂直下落，界面上有一些漏斗，一共有m个漏斗分别放在第2_{m+1行，第i个漏斗的作用是把经过第i+1行且列数在Ai}Bi之间的球，将其移到下一行的第Ci列。 使用第i个漏斗需要支付Di的价钱，你需要保留一些漏斗使得球无论从第一行的哪一列开始放，都只可能到达第m+2行的唯一 一列，求花费的最少代价。

(样例的图)

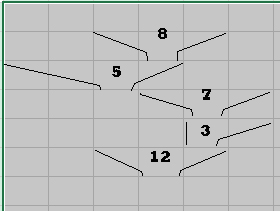
(我们保留2，4，5即可，代价为5+3+12=20)

Input

第一行两个数，m和n。m<=100000,2<=n<=1000000000

接下来m行，第i+1行描述第i个漏斗的属性，Ai,Bi,Ci,Di (1<=Ai<=Ci<=Bi<=n, 1<=Di<=1000000000)。

Output

若不存在一种方案能满足条件则输出-1，否则输出最小花费

Input示例

5 6

3 5 4 8

1 4 3 5

4 6 5 7

5 6 5 3

3 5 4 12

Output示例

20

题解

首先发现，对于一个漏斗来说，不管它上面的怎么选，它能贡献的肯定是一个区间

那么只要能够到\(1\)，又能够到\(n\)，那么就可以了

我们枚举最下面的漏斗是哪个，那么不难发现它需要两个满足\(C_i\)在\(A_i\)和\(B_i\)之间的漏斗，且一个能使它够到左边，一个能使它够到右边

简单来说，就是设\(lmn_i\)为必选第\(i\)个漏斗，且范围包含\([1,C_i]\)时的最小代价，\(rmn_i\)为必选第\(i\)个漏斗，且范围包含\([C_i,n]\)时的最小代价

然后我们枚举最下面的漏斗，答案即为满足\(A_i\leq C_j\leq B_i\)的最小的\(lmn_j\)和最小的\(rmn_j\)（两个不是同一个）

那么用线段树维护就好了

感觉比较难讲清楚，看代码比较好

//minamoto
#include<bits/stdc++.h>
#define R register
#define ll long long
#define ls (p<<1)
#define rs (p<<1|1)
#define inf 0x3f3f3f3f3f3f3f3f
#define fp(i,a,b) for(R int i=a,I=b+1;i<I;++i)
#define fd(i,a,b) for(R int i=a,I=b-1;i>I;--i)
#define go(u) for(int i=head[u],v=e[i].v;i;i=e[i].nx,v=e[i].v)
template<class T>inline bool cmax(T&a,const T&b){return a<b?a=b,1:0;}
template<class T>inline bool cmin(T&a,const T&b){return a>b?a=b,1:0;}
using namespace std;
char buf[1<<21],*p1=buf,*p2=buf;
inline char getc(){return p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++;}
int read(){
	R int res=1,f=1;R char ch;
	while((ch=getc())>'9'||ch<'0')(ch=='-')&&(f=-1);
	for(res=ch-'0';(ch=getc())>='0'&&ch<='9';res=res*10+ch-'0');
	return res*f;
}
const int N=1e5+5;
int l[N],r[N],c[N],d[N],b[N];
ll lmn[N<<2],rmn[N<<2],lx,rx,res;
int n,m,lim;
void update(int p,int l,int r,int x){
	cmin(lmn[p],lx),cmin(rmn[p],rx);
	if(l==r)return;
	int mid=(l+r)>>1;
	x<=mid?update(ls,l,mid,x):update(rs,mid+1,r,x);
}
void query(int p,int l,int r,int ql,int qr){
	if(ql<=l&&qr>=r)return cmin(lx,lmn[p]),cmin(rx,rmn[p]),void();
	int mid=(l+r)>>1;
	if(ql<=mid)query(ls,l,mid,ql,qr);
	if(qr>mid)query(rs,mid+1,r,ql,qr);
}
int main(){
	freopen("pinball.in","r",stdin);
	freopen("pinball.out","w",stdout);
	n=read(),m=read();
	fp(i,1,n)l[i]=read(),r[i]=read(),c[i]=b[i]=read(),d[i]=read();
	sort(b+1,b+1+n),lim=unique(b+1,b+1+n)-b-1;
	memset(lmn,0x3f,sizeof(lmn));
	memset(rmn,0x3f,sizeof(rmn));
	res=inf;
	fp(i,1,n){
		lx=(l[i]==1)?0:inf;
		rx=(r[i]==m)?0:inf;
		l[i]=lower_bound(b+1,b+1+lim,l[i])-b;
		r[i]=upper_bound(b+1,b+1+lim,r[i])-b-1;
		c[i]=lower_bound(b+1,b+1+lim,c[i])-b;
		query(1,1,lim,l[i],r[i]);
		cmin(res,lx+rx+d[i]);
		lx+=d[i],rx+=d[i];
		update(1,1,lim,c[i]);
	}
	printf("%lld\n",res==inf?-1:res);
	return 0;
}