最近公共祖先 Least Common Ancestors（LCA）算法 --- 与RMQ问题的转换

【简介】

LCA（T，u，v）：在有根树T中，询问一个距离根最远的结点x，使得x同时为结点u、v的祖先。

RMQ（A，i，j）：对于线性序列A中，询问区间[i，j]上的最值。见我的博客---RMQ ---- ST（Sparse Table）算法。

【LCA算法】

解决LCA问题有多种算法，一种是离线的 Tarjan算法 ，还有在线的倍增法 ，还有就是转换为RMQ问题的在线算法。

【LCA转化为RMQ】

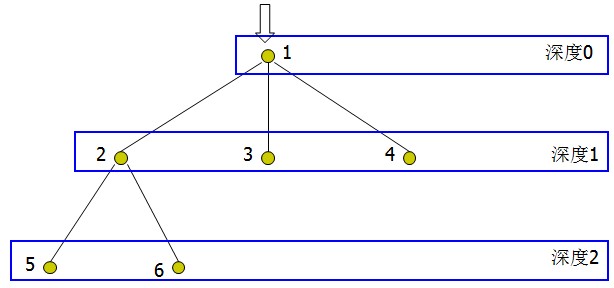
（一）对有根树T进行DFS，将遍历到的结点按照顺序记下，我们将得到一个长度为2N – 1的序列，称之为T的欧拉序列F 。

（二）每个结点都在欧拉序列中出现，我们记录结点u在欧拉序列中第一次出现的位置为pos(u)。

   根据DFS的性质，对于两结点u、v，从pos(u)遍历到pos(v)的过程中经过LCA(u, v)有且仅有一次，且深度是深度序列B[pos(u)…pos(v)]中最小的。

   即LCA(T, u, v) = RMQ(B, pos(u), pos(v))，并且问题规模仍然是O(N)的。

至此，LCA问题就转化为RMQ问题。

【RMQ转化为LCA】

简单说明下吧：考察一个长度为N的序列A，按照如下方法将其递归建立为一棵树：

1)设序列中最小值为A_k，建立优先级为Ak的根节点T_k；

2)将A(1…k–1)递归建树作为T_k的左子树；

3)将A(k+1…N)递归建树作为T_k的右子树；

    不难发现，这棵树是一棵优先级树T。

    对于RMQ(A，i，j)：

1)设序列中最小值为Ak，若k∈[i, j]，那么答案为k；

2)若k > j，那么答案为RMQ(A₁..k-1，i，j)；

3)若k < i，那么答案为RMQ(A_K+1..N，i，j)；

不难发现RMQ(A，i，j) = LCA(T，i，j)！

【例题 HDU 2586】