【JDK】JDK源码分析-TreeMap(1)

概述

前面数据结构与算法笔记对红黑树进行了分析，而 TreeMap 内部就是基于红黑树实现的。示意图：

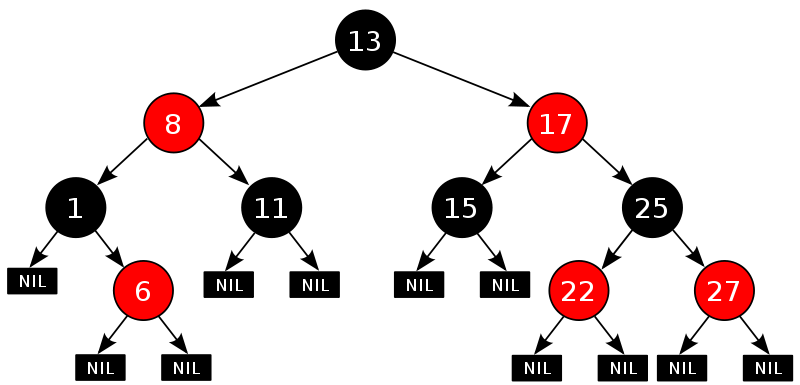
它的查找、插入、删除操作的时间复杂度均为 O(logn)。

TreeMap 类的继承结构如下：

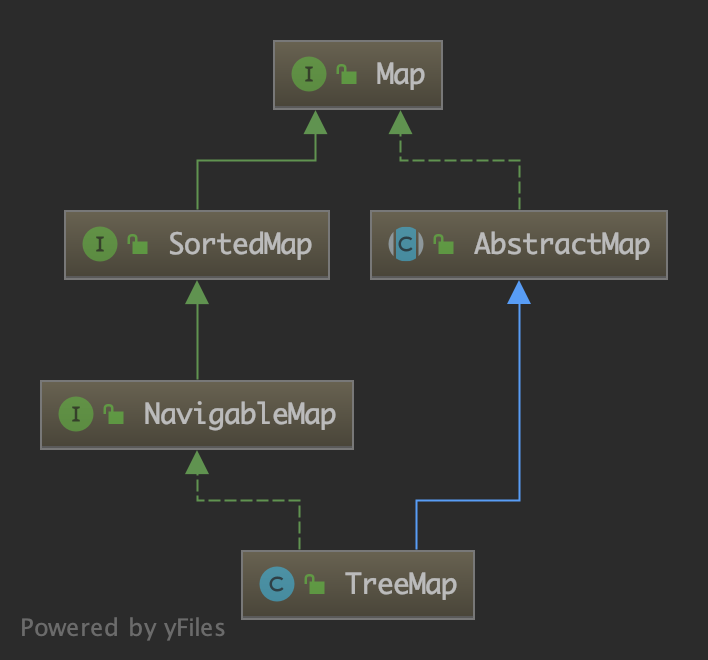
类签名：

public class TreeMap<K,V>
    extends AbstractMap<K,V>
    implements NavigableMap<K,V>, Cloneable, java.io.Serializable

TreeMap 实现了 Map 接口，其内部数据格式是“键-值对”的形式（Entry），排列顺序是按照键的顺序进行的。

代码分析

成员变量

/**
 * The comparator used to maintain order in this tree map, or
 * null if it uses the natural ordering of its keys.
 *
 * TreeMap 内部的比较器，若为空，则为自然顺序
 */
private final Comparator<? super K> comparator;

// 根节点
private transient Entry<K,V> root;

/**
 * The number of entries in the tree
 */
private transient int size = 0;

/**
 * The number of structural modifications to the tree.
 */
private transient int modCount = 0;

构造器

TreeMap 有四个构造器，分别如下：

构造器一：无参构造器

/**
 * 无参构造器。使用 key 的自然顺序排列（key 要实现 Comparable 接口）
 */
public TreeMap() {
    comparator = null;
}

构造器二：

/**
 * 使用指定的 Comparator（比较器）构造一个空的 TreeMap
 */
public TreeMap(Comparator<? super K> comparator) {
    this.comparator = comparator;
}

构造器三：

/**
 * 使用给定的 Map 构造一个 TreeMap
 */
public TreeMap(Map<? extends K, ? extends V> m) {
    comparator = null;
    putAll(m);
}

构造器四：

/**
 * 使用给定的 SortedMap 构造一个 TreeMap
 *（使用 SortedMap 的顺序）
 */
public TreeMap(SortedMap<K, ? extends V> m) {
    comparator = m.comparator();
    try {
        buildFromSorted(m.size(), m.entrySet().iterator(), null, null);
    } catch (java.io.IOException cannotHappen) {
    } catch (ClassNotFoundException cannotHappen) {
    }
}

常用方法

查找某个 key

// 判断 TreeMap 是否包含某个 key
public boolean containsKey(Object key) {
    return getEntry(key) != null;
}

// 查找 TreeMap 中某个 key 对应的 value（若不存在返回 null）
public V get(Object key) {
    Entry<K,V> p = getEntry(key);
    return (p==null ? null : p.value);
}

由于这两个方法内部都是通过 getEntry 方法实现，因此放在一起分析，如下：

final Entry<K,V> getEntry(Object key) {
    // Offload comparator-based version for sake of performance
    if (comparator != null)
        return getEntryUsingComparator(key);
    if (key == null)
        throw new NullPointerException();
    @SuppressWarnings("unchecked")
        Comparable<? super K> k = (Comparable<? super K>) key;
    Entry<K,V> p = root;
    while (p != null) {
        int cmp = k.compareTo(p.key);
        if (cmp < 0)
            p = p.left;
        else if (cmp > 0)
            p = p.right;
        else
            return p;
    }
    return null;
}

当 Comparator 不为空时，使用如下方法查找：

/**
 * Version of getEntry using comparator. Split off from getEntry
 * for performance. (This is not worth doing for most methods,
 * that are less dependent on comparator performance, but is
 * worthwhile here.)
 */
final Entry<K,V> getEntryUsingComparator(Object key) {
    @SuppressWarnings("unchecked")
        K k = (K) key;
    Comparator<? super K> cpr = comparator;
    if (cpr != null) {
        Entry<K,V> p = root;
        while (p != null) {
            int cmp = cpr.compare(k, p.key);
            if (cmp < 0)
                p = p.left;
            else if (cmp > 0)
                p = p.right;
            else
                return p;
        }
    }
    return null;
}

可以看到，这两个方法都是二叉查找树的查找过程。

PS: 这里将 Comporator 和 Comparable 两个接口分开进行操作。注释说明是出于性能考虑，虽然大部分方法中不值得这样做，但这里值得。

查找某个 value

public boolean containsValue(Object value) {
    for (Entry<K,V> e = getFirstEntry(); e != null; e = successor(e))
        if (valEquals(value, e.value))
            return true;
    return false;
}

getFirstEntry() 方法是获取第一个 Entry 节点（中序遍历最左边的节点）：

/**
 * Returns the first Entry in the TreeMap (according to the TreeMap's
 * key-sort function).  Returns null if the TreeMap is empty.
 */
final Entry<K,V> getFirstEntry() {
    Entry<K,V> p = root;
    if (p != null)
        while (p.left != null)
            p = p.left;
    return p;
}

查找某个 Entry 的后继节点：

/**
 * Returns the successor of the specified Entry, or null if no such.
 */
static <K,V> TreeMap.Entry<K,V> successor(Entry<K,V> t) {
    if (t == null)
        return null;
    // 若右子树不为空，则后继节点就是右子树的最小节点
    else if (t.right != null) {
        Entry<K,V> p = t.right;
        while (p.left != null)
            p = p.left;
        return p;
    } else {
        // 若右子树为空，则向上回溯
        Entry<K,V> p = t.parent;
        Entry<K,V> ch = t;
        while (p != null && ch == p.right) {
            ch = p;
            p = p.parent;
        }
        return p;
    }
}

可以看到，这里判断 TreeMap 是否包含某个 value，是按照二叉查找树的中序遍历去比较是否存在与给定 value 相等的值。

lowerEntry / lowerKey: 查找比指定 key 小的最大 Entry / key

public Map.Entry<K,V> lowerEntry(K key) {
    return exportEntry(getLowerEntry(key));
}

public K lowerKey(K key) {
    return keyOrNull(getLowerEntry(key));
}

/**
 * Returns the entry for the greatest key less than the specified key; if
 * no such entry exists (i.e., the least key in the Tree is greater than
 * the specified key), returns {@code null}.
 */
final Entry<K,V> getLowerEntry(K key) {
    Entry<K,V> p = root;
    while (p != null) {
        int cmp = compare(key, p.key);
        // 给定的key大于根节点，继续与右子节点比较
        if (cmp > 0) {
            if (p.right != null)
                p = p.right;
            else
                return p;
        } else {
            // 左子节点不为空，则为左子节点
            if (p.left != null) {
                p = p.left;
            } else {
                // 左子节点为空，向父节点上溯
                Entry<K,V> parent = p.parent;
                Entry<K,V> ch = p;
                while (parent != null && ch == parent.left) {
                    ch = parent;
                    parent = parent.parent;
                }
                return parent;
            }
        }
    }
    return null;
}

higherEntry / higherKey: 查找比指定 key 大的最小 Entry / key

public Map.Entry<K,V> higherEntry(K key) {
    return exportEntry(getHigherEntry(key));
}

public K higherKey(K key) {
    return keyOrNull(getHigherEntry(key));
}

getHigherEntry 方法与 getLowerEntry 方法实现类似，不同之处在于 left 和 right 相反，这里不再贴代码。

floorEntry / floorKey:

public Map.Entry<K,V> floorEntry(K key) {
    return exportEntry(getFloorEntry(key));
}

public K floorKey(K key) {
    return keyOrNull(getFloorEntry(key));
}

/**
 * Gets the entry corresponding to the specified key; if no such entry
 * exists, returns the entry for the greatest key less than the specified
 * key; if no such entry exists, returns {@code null}.
 */
final Entry<K,V> getFloorEntry(K key) {
    Entry<K,V> p = root;
    while (p != null) {
        int cmp = compare(key, p.key);
        if (cmp > 0) {
            if (p.right != null)
                p = p.right;
            else
                return p;
        } else if (cmp < 0) {
            if (p.left != null) {
                p = p.left;
            } else {
                Entry<K,V> parent = p.parent;
                Entry<K,V> ch = p;
                while (parent != null && ch == parent.left) {
                    ch = parent;
                    parent = parent.parent;
                }
                return parent;
            }
        } else
            // 与上述方法的区别
            return p;
    }
    return null;
}

查找指定 key 关联的 Entry；若不存在，返回比该 key 小的最大 key 关联的 Entry；若这也不存在则返回 null。

PS: 该方法与上面的 getLowerEntry 方法仅相差 while 循环内部的一个 else。

ceilingEntry / ceilKey:

public Map.Entry<K,V> ceilingEntry(K key) {
    return exportEntry(getCeilingEntry(key));
}

public K ceilingKey(K key) {
    return keyOrNull(getCeilingEntry(key));
}

getCeilingEntry 方法与 getFloorEntry 方法实现类似，也是 left 和 right 相反。就像上面 getLowerEntry 和 getHigherEntry的区别那样，这里不再贴代码。

查找指定 key 关联的 Entry；若不存在，返回比该 key 大的最小 key 关联的 Entry；若这也不存在则返回 null。

还有几个截取 TreeMap 一部分的方法，分别如下：

public NavigableMap<K,V> headMap(K toKey, boolean inclusive) {
    return new AscendingSubMap<>(this,
                                 true,  null,  true,
                                 false, toKey, inclusive);
}

public NavigableMap<K,V> tailMap(K fromKey, boolean inclusive) {
    return new AscendingSubMap<>(this,
                                 false, fromKey, inclusive,
                                 true,  null,    true);
}

public NavigableMap<K,V> subMap(K fromKey, boolean fromInclusive,
                                K toKey,   boolean toInclusive) {
    return new AscendingSubMap<>(this,
                                 false, fromKey, fromInclusive,
                                 false, toKey,   toInclusive);
}

除此之外，最常用的插入和删除操作还未分析，这两部分比较复杂，因此留到后面单独分析。

小结

1. TreeMap 实现了 Map 接口，内部节点类型为 Entry；

2. 基于红黑树实现，具有红黑树的特点；

3. 有序，根据 Entry 的 key 排序；

4. 查找、插入、删除操作的时间复杂度均为 O(logn)。

相关阅读

数据结构与算法笔记（四）

Stay hungry, stay foolish.

PS: 本文首发于微信公众号【WriteOnRead】。