数论 Day 13

数论_CRT（中国剩余定理）& Lucas （卢卡斯定理）

前言

又是一脸懵逼的一天。

正文

按照道理来说，我们应该先做一个介绍。

---

中国剩余定理

中国剩余定理，Chinese Remainder Theorem，又称孙子定理，给出了一元线性同余方程组的有解判定条件，并用构造法给出了通解的具体形式。

现在有方程组：中国剩余定理指出：

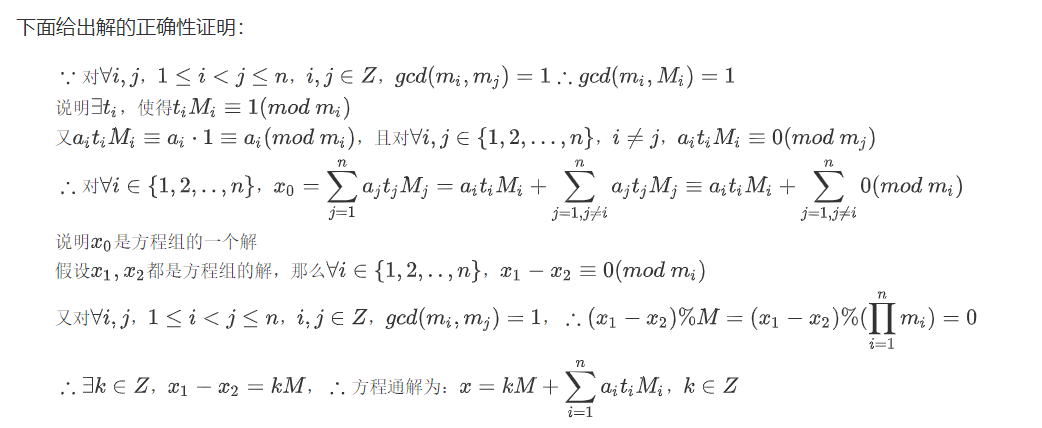
扩展中国剩余定理

在一般情况下，要求任两个数互质这个条件太苛刻了，CRT派不上用场，我们需要一个更具普遍性的结论，这就是EX-CRT。虽然是称为EX-CRT，但这个定理并没有直接用到CRT的结论。

typedef long long ll;
;
​
// m为模数组，a为余数数组，0~n-1
ll m[maxn], a[maxn];
​
ll exgcd(ll a, ll b, ll &x, ll &y) {
    ) {
        x = ; y = ;
        return a;
    }
    ll ans = exgcd(b, a % b, y, x);
    y -= a / b * x;
    return ans;
}
​
ll excrt() {
    ll lcm = m[], last_a = a[];
    ; i < n; i++) {
        ll lcm_a = ((a[i] - last_a) % m[i] + m[i]) % m[i];
        ll k = lcm, x, y;
        ll gcd = exgcd(lcm, m[i], x, y);
        ll mod = m[i] / gcd;
        x = (x * lcm_a / gcd % mod + mod) % mod;
        lcm = lcm / gcd * m[i], last_a = (last_a + k * x) % lcm;
    }
    return (last_a % lcm + lcm) % lcm;
}

卢卡斯定理

卢卡斯定理是关于组合数和同余的定理，它表明当p为素数时：

其中，即为的进制展开中对应次数为的系数

因为当m>n时，二项式系数为0，那么二项式系数即组合数能被p整除等价于在p进制下，存在某一位m的数值大于对应的n的数值。

基于母函数可以简单证明这个定理。

可以用除法和取模方便的在循环中求出各个系数，代码如下：

typedef long long ll;
;
;
​
void init() {
    F[] = ;
    ; i < maxn; i++)
        F[i] = i * F[i - ] % mod;
}
​
ll qpow(ll a, ll b) {
    ll ans = ;
    while(b) {
        ) ans = ans * a % mod;
        b >>= ; a = a * a % mod;
    }
    return ans;
}
​
ll lucas(ll N, ll M) {
    ll ans = ;
    while(N & M) {
        ll n = N % mod, m = M % mod;
        ;
        ans = ans * F[a] % mod * qpow(F[m] * F[n - m] % mod, mod - ) % mod;
        N /= p; M /= p;
    }
    return ans;
}

扩展卢卡斯定理

卢卡斯定理同样不能处理模数不是素数的情况，这时便需要扩展卢卡斯定理。我们一步步分析如何求解模数不是素数的组合数问题。

首先，我们要解决的问题是求，其中不一定是素数。对于非素数，我们首先会联想到质因分解后结合解决问题。假设分解得到个质数，质数对应的个数为，对质因分解有。显然对，，，假设对，我们求出了，那么我们可以得到同余方程组：：这时我们便可以套用解决问题，那么问题便转化为如何求解。

---

现在我们要求的是，其中是素数。又，显然需要求出和关于模的逆元，但考虑到这些项中可能包含（含有则不互质，逆元不存在），所以需要先提取，得到：，这里的阶乘是指提取之后的结果。这时就可以计算和关于的逆元了。这里，为了形式的统一，同时提取了中的。那么，问题又转化为了如何求。

---

目标：计算，为质数。上一步中提到，我们需要先提取。提取结果为：。第一部分很好理解，对于每一个的倍数，都可以提取出一个，一共有个；第二部分为的倍数被提取之后余下的，是一个阶乘的形式。显然在中，对于的幂，的个数不止个，也就是说第二部分仍然需要提取，这一部分可以递归解决。第三部分是剔除了的倍数之后余下的。对，，都有对，这也就是说，第三部分其实是存在循环节的，一共循环了次。除去循环节的余项长度在之内，直接累乘即可。

完整代码如下：

typedef long long ll;
;
​
ll n, m, p;
​
ll qpow(ll a, ll b, ll mod) {
    ll ans = ;
    while(b) {
        ) ans = ans * a % mod;
        b >>= ; a = a * a % mod;
    }
    return ans;
}
​
ll fac(ll n, ll p, ll pk) {
    ;
    ll ans = ;
    ; i < pk; i++)
        if (i % p) ans = ans * i % pk;
    ans = qpow(ans, n / pk, pk);
    int npk = n % pk;
    ; i <= npk; i++)
        if (i % p) ans = ans * i % pk;
    return ans * fac(n / p, p, pk) % pk;
}
​
ll exgcd(ll a, ll b, ll &x, ll &y) {
    ) {
        x = ; y = ;
        return a;
    }
    ll ans = exgcd(b, a % b, y, x);
    y -= a / b * x;
    return ans;
}
​
ll inv(ll a, ll p) {
    , p);
}
​
ll C(ll n, ll m, ll p, ll pk) {
    ;
    ll fn = fac(n, p, pk),
       fm = fac(m, p, pk),
       fn_m = fac(n - m, p, pk),
       cnt = ;
    for (ll i = n; i; i /= p)
        cnt += i / p;
    for (ll i = m; i; i /= p)
        cnt -= i / p;
    for (ll i = n - m; i; i /= p)
        cnt -= i / p;
    return fn * inv(fm * fn_m % pk, pk) % pk * qpow(p, cnt, pk) % pk;
}
​
ll a[N], mod[N]; // a[]是通过卢卡斯分解出来的组合数值，m[]是对应的模数
int cnt; // 质因数的种数
​
ll CRT() {
    ll M = , ans = ;
    ; i < cnt; i++)
        M *= mod[i];
    ; i < cnt; i++)
        ans = (ans + a[i] * (M / mod[i]) % M * inv(M / mod[i], mod[i]) % M) % M;
    return ans;
}
​
ll exlucas(ll n, ll m, ll p) {
    ll sqrtp = sqrt(p + 0.5);
    ; p >  && i <= sqrtp; i++) {
        ll pk = ;
        )
            p /= i, pk *= i;
        )
            a[cnt] = C(n, m, i, pk), mod[cnt++] = pk;
    }
    )
        a[cnt] = C(n, m, p, p), mod[cnt++] = p;
    return CRT();
}

---

题目

其实这篇博客到这里几乎就可以没了，因为我。。。爆0了

难啊。。。

A题

Some people believe that there are three cycles in a person's life that start the day he or she is born. These three cycles are the physical, emotional, and intellectual cycles, and they have periods of lengths 23, 28, and 33 days, respectively. There is one peak in each period of a cycle. At the peak of a cycle, a person performs at his or her best in the corresponding field (physical, emotional or mental). For example, if it is the mental curve, thought processes will be sharper and concentration will be easier.

Since the three cycles have different periods, the peaks of the three cycles generally occur at different times. We would like to determine when a triple peak occurs (the peaks of all three cycles occur in the same day) for any person. For each cycle, you will be given the number of days from the beginning of the current year at which one of its peaks (not necessarily the first) occurs. You will also be given a date expressed as the number of days from the beginning of the current year. You task is to determine the number of days from the given date to the next triple peak. The given date is not counted. For example, if the given date is 10 and the next triple peak occurs on day 12, the answer is 2, not 3. If a triple peak occurs on the given date, you should give the number of days to the next occurrence of a triple peak.

This problem contains multiple test cases!

The first line of a multiple input is an integer N, then a blank line followed by N input blocks. Each input block is in the format indicated in the problem description. There is a blank line between input blocks.

The output format consists of N output blocks. There is a blank line between output blocks.

Input

You will be given a number of cases. The input for each case consists of one line of four integers p, e, i, and d. The values p, e, and i are the number of days from the beginning of the current year at which the physical, emotional, and intellectual cycles peak, respectively. The value d is the given date and may be smaller than any of p, e, or i. All values are non-negative and at most 365, and you may assume that a triple peak will occur within 21252 days of the given date. The end of input is indicated by a line in which p = e = i = d = -1.

Output

For each test case, print the case number followed by a message indicating the number of days to the next triple peak, in the form:

Case 1: the next triple peak occurs in 1234 days.

Use the plural form ``days'' even if the answer is 1.

Sample Input

1

0 0 0 0 0 0 0 100 5 20 34 325 4 5 6 7 283 102 23 320 203 301 203 40 -1 -1 -1 -1

Sample Output

Case 1: the next triple peak occurs in 21252 days. Case 2: the next triple peak occurs in 21152 days. Case 3: the next triple peak occurs in 19575 days. Case 4: the next triple peak occurs in 16994 days. Case 5: the next triple peak occurs in 8910 days. Case 6: the next triple peak occurs in 10789 days.

Biorhythms HDU-1370

题意

一个人有三个值（不知道是啥），然后每个值每到一个周期就会到达顶峰，求从d天开始，他三个值都到达顶峰是第几天。

思路

然而，三个周期都是质数，显然用的是中国剩余定理（CRT）

抽象一点来说，就是给你三个同余方程。

代码

 #include <iostream>
 #include <cstdio>
 #include <algorithm>
 #include <cmath>
 #include <cstring>
 using namespace std;
 typedef long long ll;
 ll exgcd(ll a, ll b, ll &x, ll &y)
 {
     if(!b)
     {
         x = ;
         y =  * ;
         return a;
     }
     ll d = exgcd(b, a % b, x, y);
     ll t = x;
     x = y;
     y = t - a / b * y;
 ​
     return d;
 }

 ll inv(ll a,ll n)
 {
     ll y, d, x, fre, pf, qw;
     /*cnt't*/
     fre = pf = qw = ;
     fre++, pf++, qw++;
     /*can't*/
     d = exgcd(a,n,x,y);
      ? (x + n) % n:-;
 }
 ​
 ll CN(ll leo, ll *a, ll *m)
 {
     ll M = , ret = ;
     ; i < leo; i ++)
         M *= m[i];
 ​
     ; i < leo; i ++)
     {
         ll w = M / m[i];
         ret = (ret + w * inv(w, m[i]) * a[i]) % M;
     }
     return (ret + M) % M;
 }
 int main()
 {
     ll t = , d;
     ll a[],m[];
     m[] = ;
     m[] = ;
     m[] = ;
     /*GN*/
     ll tea;
     scanf("%lld", &tea);
     while(true)
     {
         scanf(], &a[], &a[], &d);
 ​
         ] == - && a[] == - && a[] == - && d == -)
             break;
         ll ans = CN(, a, m);
         if(ans <= d)
             ans += ;
         ans -= d;
 ​
         printf("Case %lld: the next triple peak occurs in %lld days.\n", t, ans);
         t++;
     }
     ;
 }

B题

F(x) is a polynomial in x with integer coefficients, here F(x) = (1+x)^a1 + (1+x)^a2 + ... + (1+x)^am. Given a1, a2, ... , am, find number of odd coefficients of F(x).

Input

The first line contains a single positive integer T( T <= 10000 ), indicates the number of test cases. For each test case: First line contains an integer N(1 <= N <= 15). Second line contains N integers a1, a2, ..., am ( 0 <= ai <= 2^45 )

Output

For each test case: output the case number as shown and an the odd coefficients of F(x).

Sample Input

4 1 1 1 3 2 1 3 3 1 2 3

Sample Output

Case #1: 2 Case #2: 4 Case #3: 2 Case #4: 2

Hint

Case #3: (1+x) + (1+x)^3 = 2 + 4x + 3x^2 + x^3. it contains 2 odd coefficients. Case #4: (1+x) + (1+x)^2 + (1+x)^3 = 3 + 6x + 4x^2 + x^3. it contains 2 odd coefficients.

Big Coefficients HDU-3929

题意

略

思路

显然是用卢卡斯，但我不知道为哈

未完待续