[Noip1997] 棋盘问题（2）

题目描述

在N×NN \times NN×N的棋盘上(1≤N≤10)(1≤N≤10)(1≤N≤10)，填入1,2,…,N21,2,…,N^21,2,…,N2共N2N^2N2个数，使得任意两个相邻的数之和为素数。

例如：当N=2N=2N=2时，有：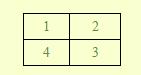

其相邻数的和为素数的有：

1+2,1+4,4+3,2+31+2,1+4,4+3,2+31+2,1+4,4+3,2+3

当N=4N=4N=4时，一种可以填写的方案如下：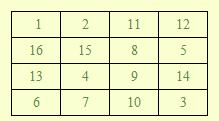

在这里我们约定：左上角的格子里必须填数字111。

输入输出格式

输入格式：

一个数NNN

输出格式：

如有多种解，则输出第一行、第一列之和为最小的排列方案；若无解，则输出“NO”。

输入输出样例

输入样例#1： 复制

1

输出样例#1： 复制

NO

输入样例#2： 复制

2

输出样例#2： 复制

1 2

---

一开始没看到第一行和第一列的和最小，一直以为只用第一列的和最小...
其实都差不多...
就是正常的搜索， 加上一维判断是不是第一列第一行搜完了。
我采取的策略是先搜第一行第一列，然后从(2, 2)点开始搜索。

---

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
using namespace std;
#define reg register
inline int read() {
    int res=;char ch=getchar();
    while(!isdigit(ch)) ch=getchar();
    while(isdigit(ch))res=(res<<)+(res<<)+(ch^),ch=getchar();
    return res;
}

int n;
bool is[*];
int use[];
int a[][];

inline void dfs(int x, int y, int end, int beg)
{
    //printf("%d %d\n", x, y);
    if (end) {
        for (reg int i =  ; i <= n ; i ++, puts(""))
            for (reg int j =  ; j <= n ; j ++)
                printf("%d ", a[i][j]);
        exit();
    }
    bool flag = ;
    for (reg int i =  ; i <= n * n ; i ++)
    {
        if (use[i]) continue;
        if ((x ==  or is[i+a[x-][y]]) and (y ==  or is[i+a[x][y-]]))
        {
            int x1 = x, y1 = y + ;
            if (beg) {
                if (x ==  and y >= ) x1 = , y1 = y + ;
                if (y ==  and x >= ) x1 = x + , y1 = ;
                if (x ==  and y == n) x1 = , y1 = ;
            }
            flag = ;
            int tmp = , tmp2 = beg;
            if (x == n and y == n) tmp = ;
            if (x == n and y == ) tmp2 = , x1 = , y1 = ;
            if (!beg and y == n and x != n) x1 = x + , y1 = ;
            a[x][y] = i;
            use[i] = ;
            dfs(x1, y1, tmp, tmp2);
            use[i] = ;
            a[x][y] = ;
        }
    }
    if (!flag) return ;
}

int main()
{
    n = read();
    if (n == ) return puts("NO"), ;
    for (reg int i =  ; i <= n * n *  ; i ++)
    {
        for (reg int j =  ; j * j <= i ; j ++)
            if (i % j == ) {is[i] = ;goto End;}
        is[i] = ;
        End:;
    }
    a[][] = ;
    use[] = ;
    dfs(, , , );
    puts("NO");
    return ;
}