绝对是全网最好的Splay 入门详解——洛谷P3369&BZOJ3224: Tyvj 1728 普通平衡树 包教包会

平衡树是什么东西想必我就不用说太多了吧。

百度百科：

一个月之前的某天晚上，yuli巨佬为我们初步讲解了Splay，当时接触到了平衡树里的旋转等各种骚操作，感觉非常厉害。而第二天我调Splay的模板竟然就搞了一天，最后还是失败告终，只能CV了事，而Splay也成了我心中的一个心结，一直没法解决。在西安集训的时候也没有去自己亲自地把Splay调出来AC，后来又面临期末考试，直到今天，我再一次地尝试将Splay调出来，又花了2个多小时的时间。这个过程是非常痛苦的，翻了无数篇博客，看了无数题解，我才勉强打出了适合我自己的Splay模板。

　　看到AC的那一瞬间，心里面是五味杂陈，虽然我是如此垃圾，现在我才自己将这样的模板A掉，但看了网上那么多篇博客，学了很多种方法，但适合我自己的我却花了很长的时间才完成。所以我希望写一篇博客，真真正正地手把手教大家Splay（仅仅是模板），让学Splay的神犇们少走一些弯路。这也许就是我这一篇博客的意义所在吧。

来看洛谷的题面：

基本操作简介：

维护的数组：

size[]：子树的大小

cnt[]：某个节点出现的次数

fa[]：某个节点它的父亲节点

val[]：某个节点对应的权值

lc[]：该节点的左儿子

rc[]：该节点的右儿子

变量：

root 根

tot 统计节点数

函数：

clear:用于删除节点时的清空

代码如下：

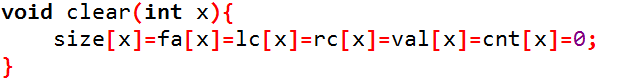
push：随时需要更新

代码如下：

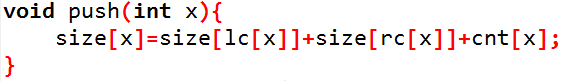
　　我们看到插入，删除等操作，就自然而然地想到用平衡树来解决它，而要完成这样的操作，最重要的核心步骤就是旋转。而旋转又分为Zig右旋和Zag左旋

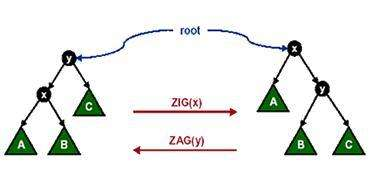
　　大家看这张图还是比较清晰明确的，其实旋转可以这样理解，一家人，x是儿子，y是x的爸爸，而z是x的爷爷，有一天，一种神奇的力量改变了他们之间的这种关系，本来是儿子的x变成了它本身父亲y的父亲，而x的爷爷z就变成了x的新父亲。

　　按照上图，我们将x右旋，x的父亲y此时就变成了它的右儿子。而x本身已经有一个右儿子了，这个右儿子就通过旋转变成了y的左儿子。而左旋的话就同理可得，x的父亲y就变成了他的左儿子，而本身x的左儿子又变成了它原来父亲y的右儿子。这样在旋转过后整个结构仍然满足之前的平衡性质。

　　旋转zig和zag的代码我都习惯分开写，两个的实现起来都差不多，比较好理解。

zig:

zag同zig也是基本相同：

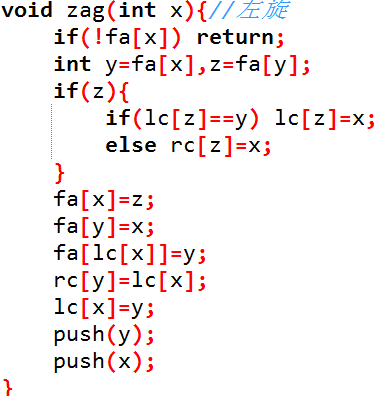
　　zig和zag在这里已经讲明白了，那么就应该是核心Splay伸展操作了,也是基于zig和zag之上的，就是将我们要操作的那个点x旋转到指定节点（一般是根节点为保证复杂度）的位置。但我们在这里还需要有一些分类讨论。

　　首先看x的爷爷z是否已经在我们需要的节点上了，如果在的话，x就只需要旋转两次就可以到指定节点的下方。

那么我们现在就需要看一看x，y，z之间的相对位置。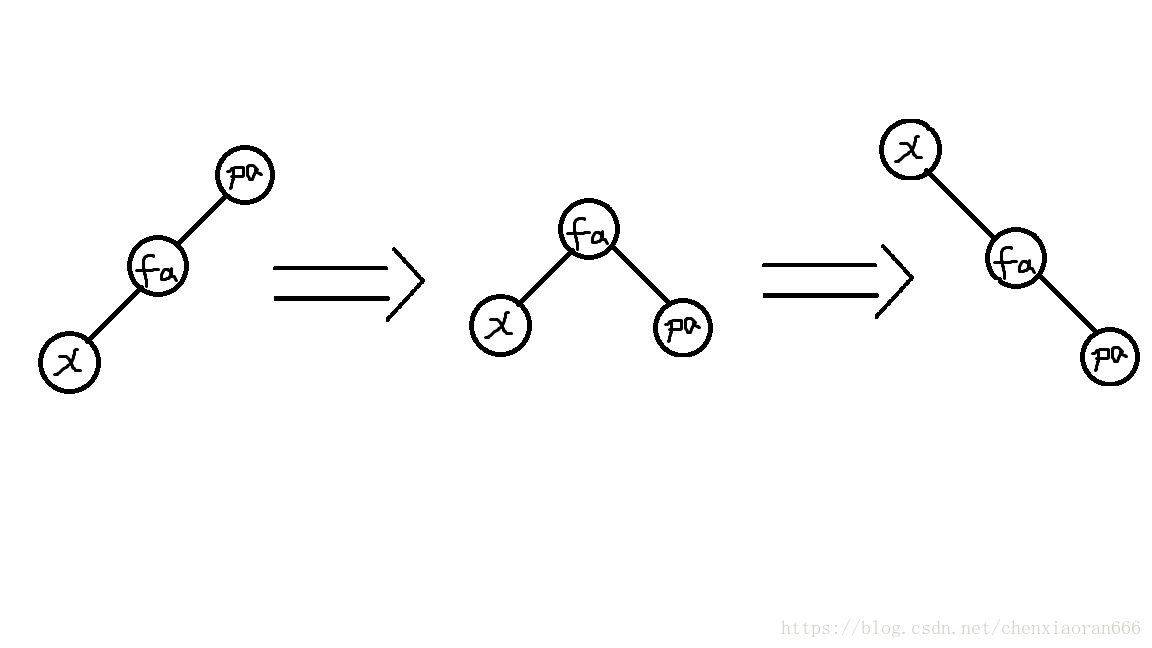

1：若x是y的左儿子，y是z的左儿子(借用某大佬博客中的图片，感谢)

此时x,y,z在同一条直线上，所以我们要将x和y都旋转zig-zig

代码片段：

2：若x是y的右儿子，y是z的右儿子，即也是在同一条直线上，那么结果和第一种情况相同，只不过应该是zag-zag

同样给出代码：

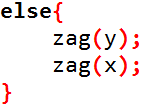
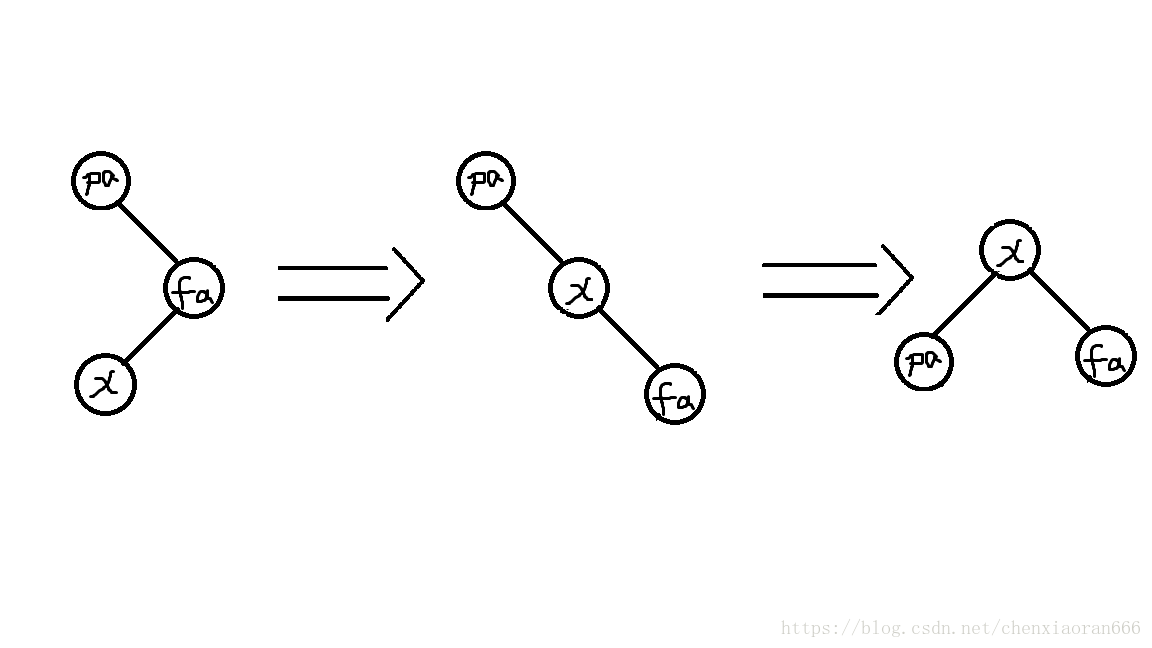
那当它们不再同一条直线上，又怎么办呢，图示已经给出来了，我们只需要转x就可以了。

显而易见的引出第三种情况x是y的右儿子，y是z的左儿子，所以我们先将x左旋，变成y的左儿子，再将x右旋到目标节点，这样就是zag-zig，代码如下：

第4中情况也就可以类比然后得出，x是y的左儿子，y是z的右儿子，这样就将x先右旋，再将其左旋，即为zig-zag操作，代码如下：

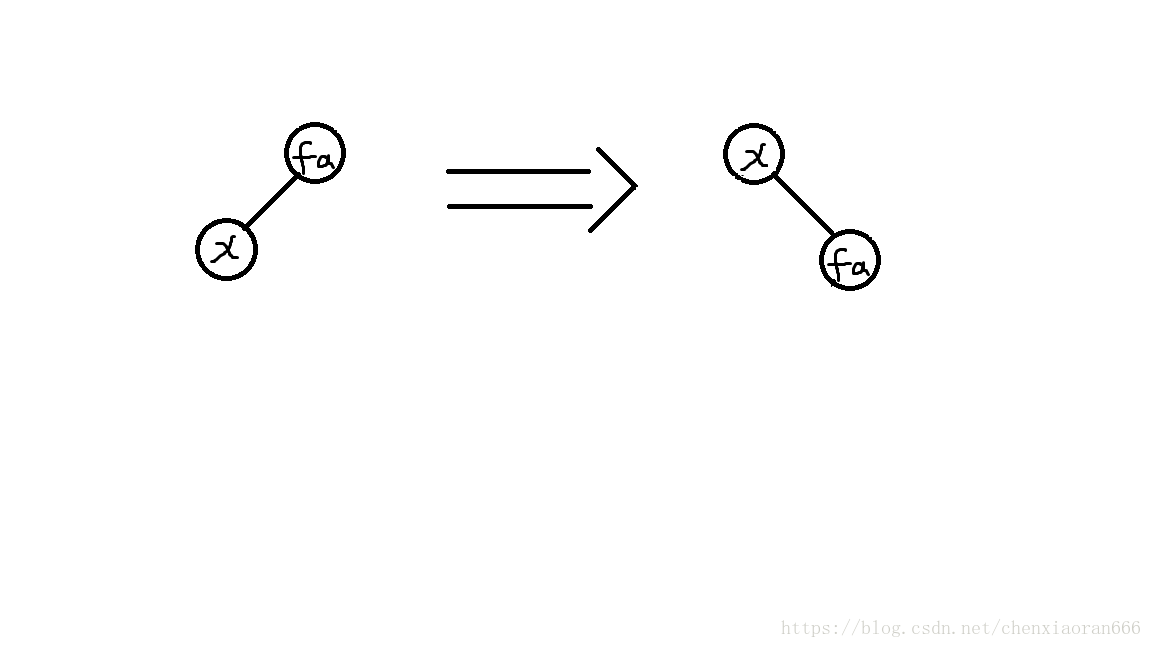
需要转两次的4种情况讲完了，那转一次就更简单了，如上图，y是目标节点，x转一下就登天了，如果x是y的右儿子，那就左旋，反之，如果是左儿子，那么他就右旋。

代码如下：

如果最后连x的父亲都是0了，那它肯定就转到根节点上了，大功告成！

完整代码如下：

接下来是insert操作：

如果此时根节点为空，说明树也为空，那么就新开一个节点，当前的节点就作为根节点。

代码如下：

此时如果已经有元素在树上了，我们就需要按照平衡树的性质（左儿子的值小于父亲，右儿子的值大于父亲）将其插入进去。从根节点开始往下找合适的位置。最后千万不要忘了更新。

我们需要插入的值如果之前已经有了，那么我们只需要将这个值出现的次数加1即可。再把这个节点旋到根。代码如下：

按一般的情况，就是以平衡树的性质插入即可。如果走到了空节点，将它插入，还需要更新其父亲的信息

维护两个变量，也可以理解为在树上的两个指针，一个是指向当前节点（从根节点开始），另一个是指向当前节点的父亲，最后还要将操作的节点旋到根。

代码如下：

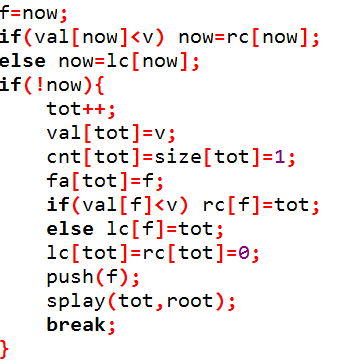
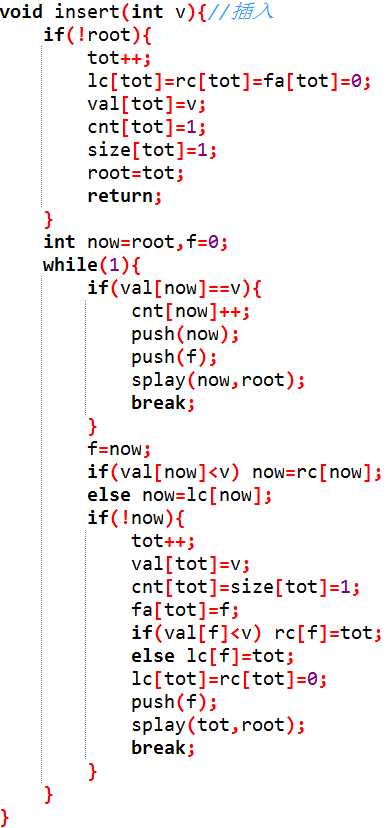
完整的insert操作如下：

好啦，接下来又是与插入操作对应的删除操作。

先求出该点对应的排名，因为之后会用到，此时x已经在根节点root上了。

如果这个点早就出现过，即cnt[x]>1，那么cnt[x]－1，直接删除就得了。

代码如下：

针对一些特殊的情况，还需要繁杂的分类讨论，这是删除操作的难点所在。

1：没有左儿子和右儿子，孤身一人，直接清空即可。

代码如下：

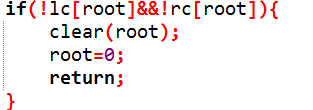
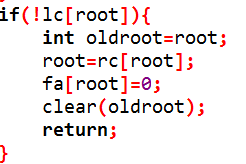
2：没有左儿子，更新现在的根节点，删去老的根节点即可。

现在的树就是这样：

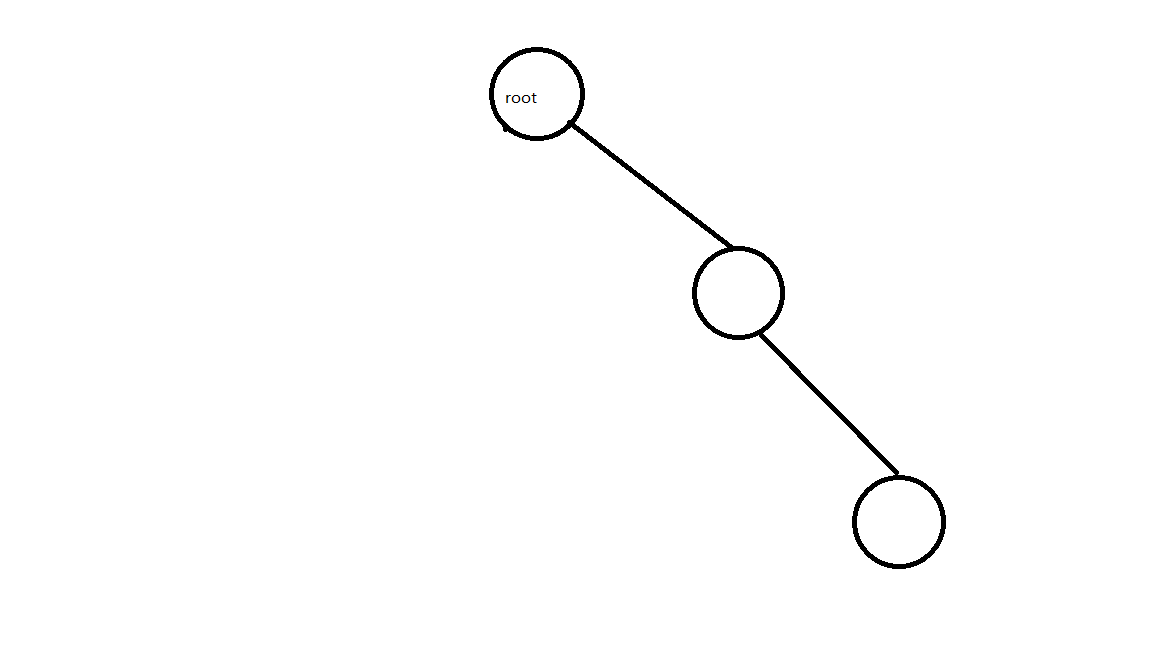
代码如下：

3：没有右儿子，同2操作。

树是这样的：

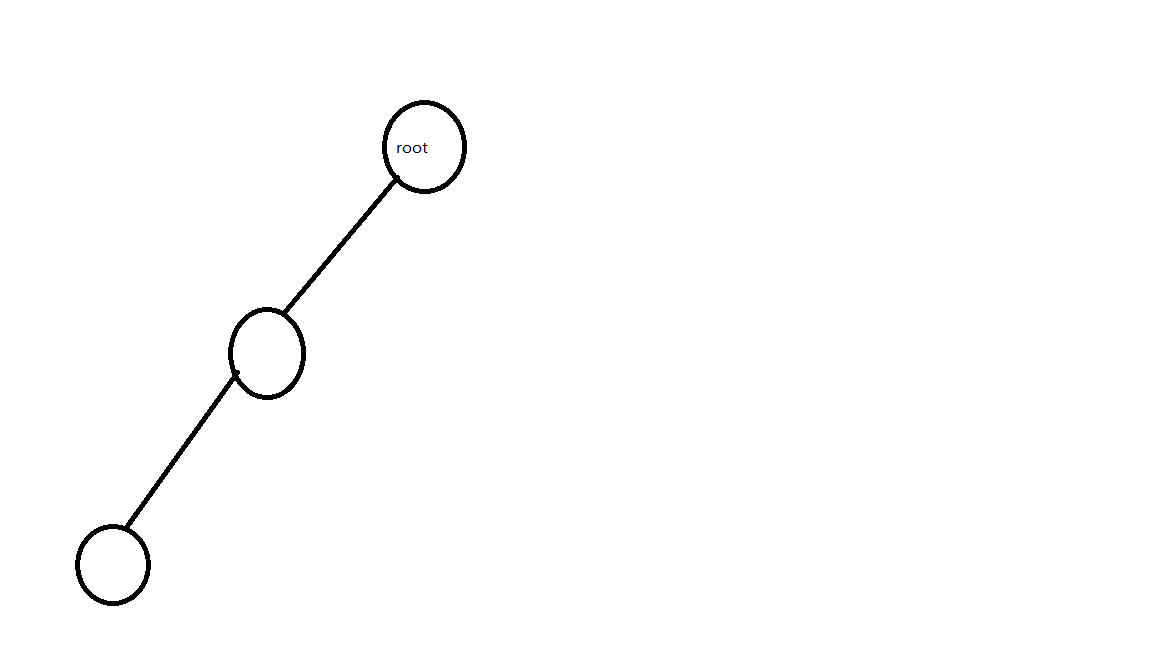
代码如下：

一般的情况：

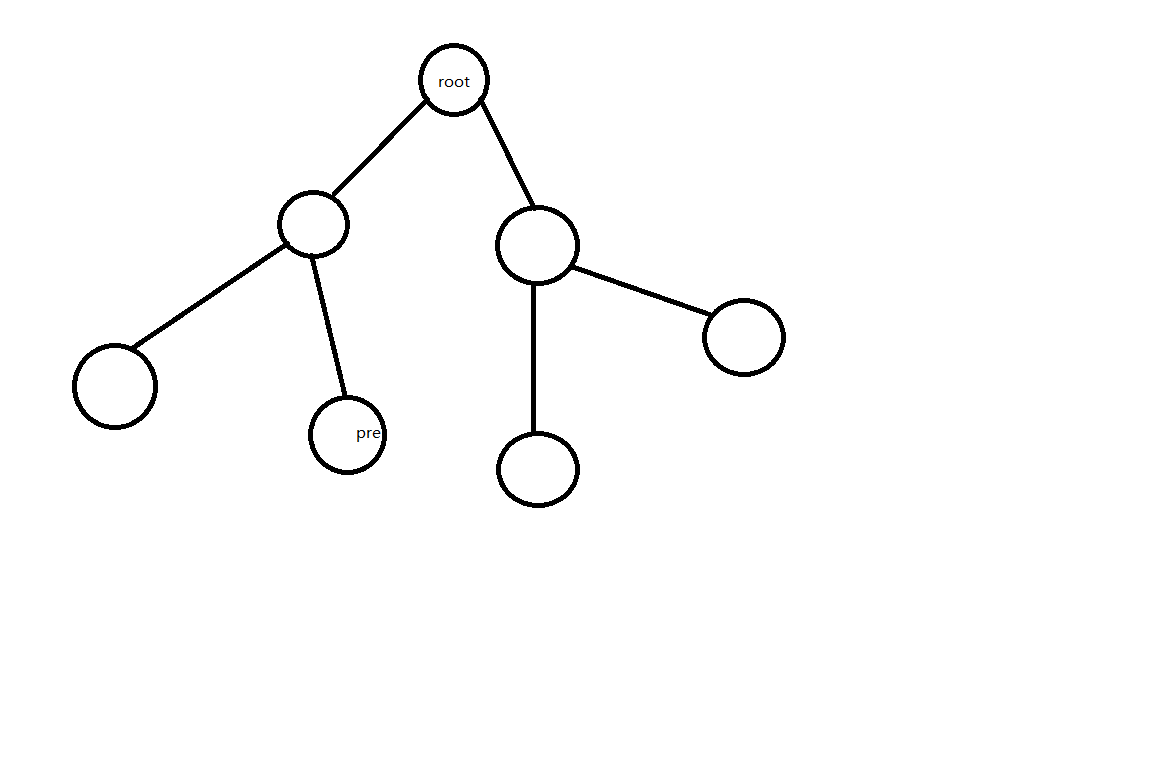
在这种情况下，我们需要求出根节点的前驱（小于x点中最大的数）然后将前驱节点Splay到根，这样也同时能够保证树的平衡。整棵右子树就成了新的根的右儿子，这样的话原来的老根就排除出外了，直接clear即可。

代码如下：

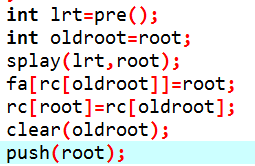
删除操作的完整版：

查询排名：

这其实很好的利用到了平衡树的性质。我们同样用一个now指针在树上找，如果值比它小就走左子树，大的话就往右子树走，走的时候累加左子树的size大小。若有多个重复的数，还要在排名中加上该数出现的次数。

代码如下图所示：

查找排名为k的数实际上就与排名的查询一个道理，但细节上也有不同。

如果当前点有左子树，并且x比左子树的大小小的话，即向左子树寻找；
否则，向右子树寻找：先判断是否有右子树，然后记录右子树的大小以及当前点的大小（都为权值），用于判断是否需要继续向右子树寻找。如果当前点有左子树，并且x比左子树的大小小的话，即向左子树寻找。

前驱和后继的查找道理就非常简单，我的代码也简单易懂，直接把查询的点插入作为根节点，从根节点向下找，最后删除即可。

Splay其实还是很简单的是不是。

完整代码见下方：

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e6+;
int fa[maxn],lc[maxn],rc[maxn],val[maxn],cnt[maxn],size[maxn];
int root,tot;
int n,opt,x;
void clear(int x){
    size[x]=fa[x]=lc[x]=rc[x]=val[x]=cnt[x]=;
}
void push(int x){
    size[x]=size[lc[x]]+size[rc[x]]+cnt[x];
}
void zig(int x){//右旋
    if(!fa[x]) return;
    int y=fa[x],z=fa[y];
    if(z){
        if(lc[z]==y) lc[z]=x;
        else rc[z]=x;
    }
    fa[x]=z;
    fa[y]=x;
    fa[rc[x]]=y;
    lc[y]=rc[x];
    rc[x]=y;
    push(y);
    push(x);
}
void zag(int x){//左旋
    if(!fa[x]) return;
    int y=fa[x],z=fa[y];
    if(z){
        if(lc[z]==y) lc[z]=x;
        else rc[z]=x;
    }
    fa[x]=z;
    fa[y]=x;
    fa[lc[x]]=y;
    rc[y]=lc[x];
    lc[x]=y;
    push(y);
    push(x);
}
void splay(int x,int rt){//伸展
    rt=fa[rt];
    int y,z;
    while(fa[x]!=rt){
        y=fa[x];
        z=fa[y];
        if(z&&z!=rt){
            if(lc[z]==y&&lc[y]==x){
                zig(y);
                zig(x);
            }
            else if(lc[z]==y&&rc[y]==x){
                zag(x);
                zig(x);
            }
            else if(rc[z]==y&&lc[y]==x){
                zig(x);
                zag(x);
            }
            else{
                zag(y);
                zag(x);
            }
        }
        else if(lc[y]==x){
            zig(x);
        }
        else{
               zag(x);
        }
    }
    if(!fa[x]) root=x;
}
void insert(int v){//插入
    if(!root){
        tot++;
        lc[tot]=rc[tot]=fa[tot]=;
        val[tot]=v;
        cnt[tot]=;
        size[tot]=;
        root=tot;
        return;
    }
    int now=root,f=;
    while(){
        if(val[now]==v){
            cnt[now]++;
            push(now);
            push(f);
            splay(now,root);
            break;
        }
        f=now;
        if(val[now]<v) now=rc[now];
        else now=lc[now];
        if(!now){
            tot++;
            val[tot]=v;
            cnt[tot]=size[tot]=;
            fa[tot]=f;
            if(val[f]<v) rc[f]=tot;
            else lc[f]=tot;
            lc[tot]=rc[tot]=;
            push(f);
            splay(tot,root);
            break;
        }
    }
}
int find1(int v){//查询v的排名
    int now=root,ans=;
    while(){
        if(v<val[now]) now=lc[now];
        else{
            ans+=size[lc[now]];
            if(v==val[now]){
                splay(now,root);
                return ans+;
            }
            ans+=cnt[now];
            now=rc[now];
        }
    }
}
int find2(int x){//查询排名为x数的值
    int now=root;
    while(){
        if(lc[now]&&x<=size[lc[now]]) now=lc[now];
        else{
            int ans=size[lc[now]]+cnt[now];
            if(ans>=x) return val[now];
            x-=ans;
            now=rc[now];
        }
    }
}
int pre(){//查找前驱和后继
    int now=lc[root];
    while(rc[now]) now=rc[now];
    return now;
}
int nex(){
    int now=rc[root];
    while(lc[now]) now=lc[now];
    return now;
}
void del(int x){//删除某个数
    find1(x);
    if(cnt[root]>){
        cnt[root]--;
        push(root);
        return;
    }
    if(!lc[root]&&!rc[root]){
        clear(root);
        root=;
        return;
    }
    if(!lc[root]){
        int oldroot=root;
        root=rc[root];
        fa[root]=;
        clear(oldroot);
        return;
    }
    if(!rc[root]){
        int oldroot=root;
        root=lc[root];
        fa[root]=;
        clear(oldroot);
        return;
    }
    int lrt=pre();
    int oldroot=root;
    splay(lrt,root);
    fa[rc[oldroot]]=root;
    rc[root]=rc[oldroot];
    clear(oldroot);
    push(root);
}
int main(){
    scanf("%d",&n);
    for(int i=;i<=n;i++){
        scanf("%d%d",&opt,&x);
        if(opt==) insert(x);
        if(opt==) del(x);
        if(opt==) printf("%d\n",find1(x));
        if(opt==) printf("%d\n",find2(x));
        if(opt==) insert(x),printf("%d\n",val[pre()]),del(x);
        if(opt==) insert(x),printf("%d\n",val[nex()]),del(x);
    }
    return ;
}