算法学习记录-图——最小路径之Floyd算法

floyd算法：

解决任意两点间的最短路径的一种算法，可以正确处理有向图或负权的最短路径问题，同时也被用于计算有向图的传递闭包。

设为从到的只以集合中的节点为中间节点的最短路径的长度。

1. 若最短路径经过点k，则；
2. 若最短路径不经过点k，则。

因此，。

在实际算法中，为了节约空间，可以直接在原来空间上进行迭代，这样空间可降至二维。

我的理解为：

folyd算法是每次选定一个点，查看任意两个顶点的距离是否都小于经过这个点之和的距离。

即：假如ABC三个顶点相连，选定C的时候，查AB的距离是否大于 AC + CB 的距离之和，

如果大于说明找到了一个更短的路径，即A->C->B。

下面是我的例子：

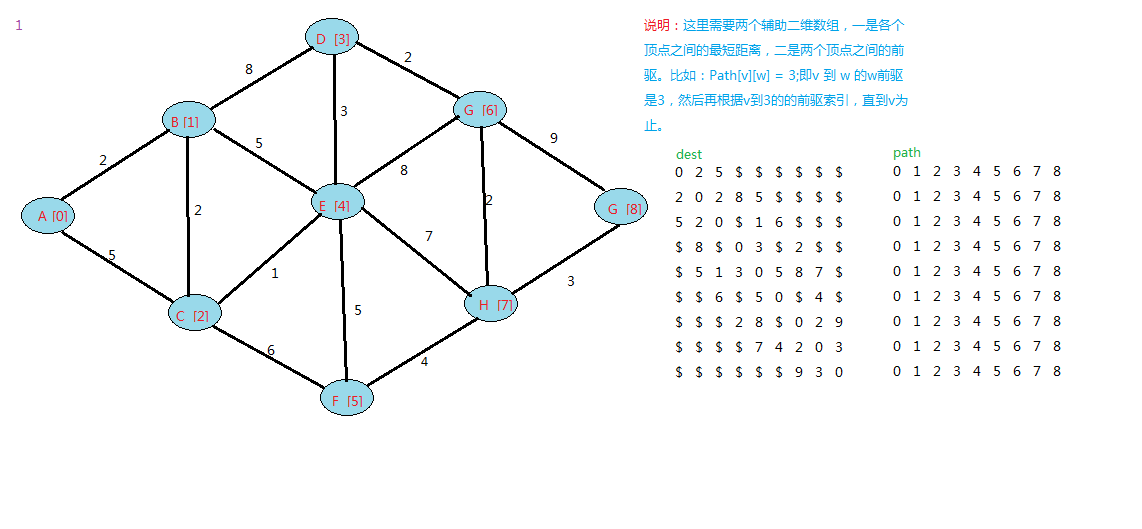
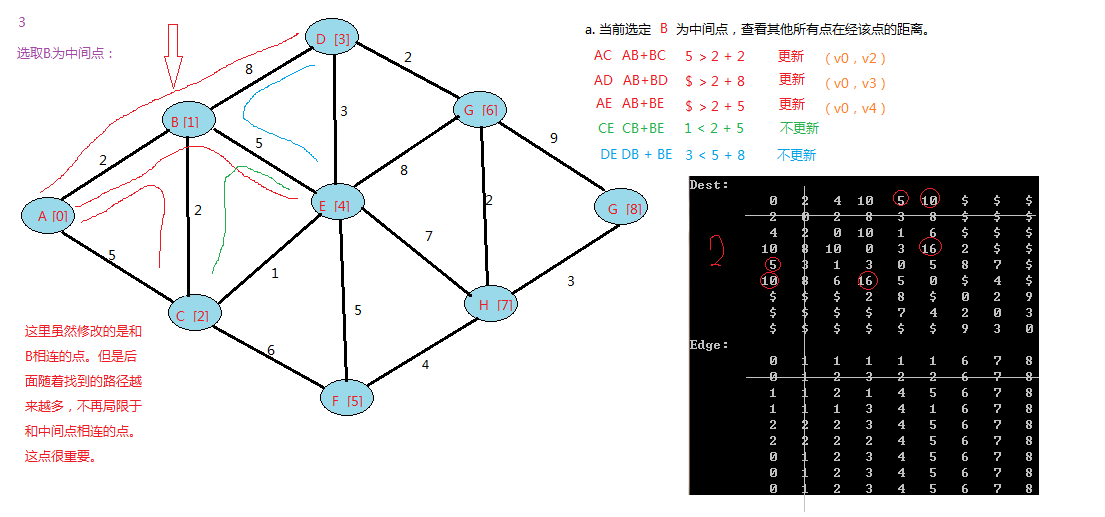
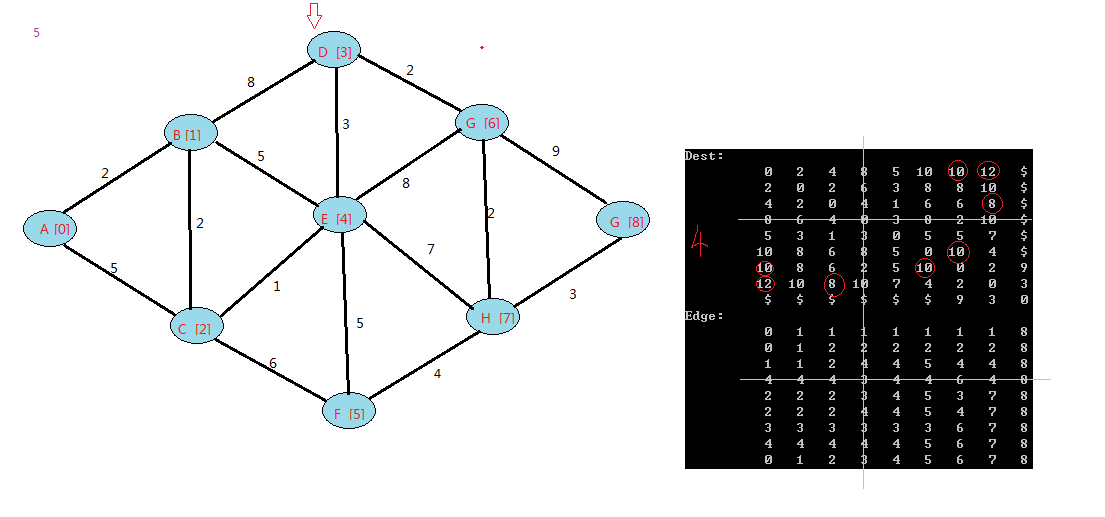
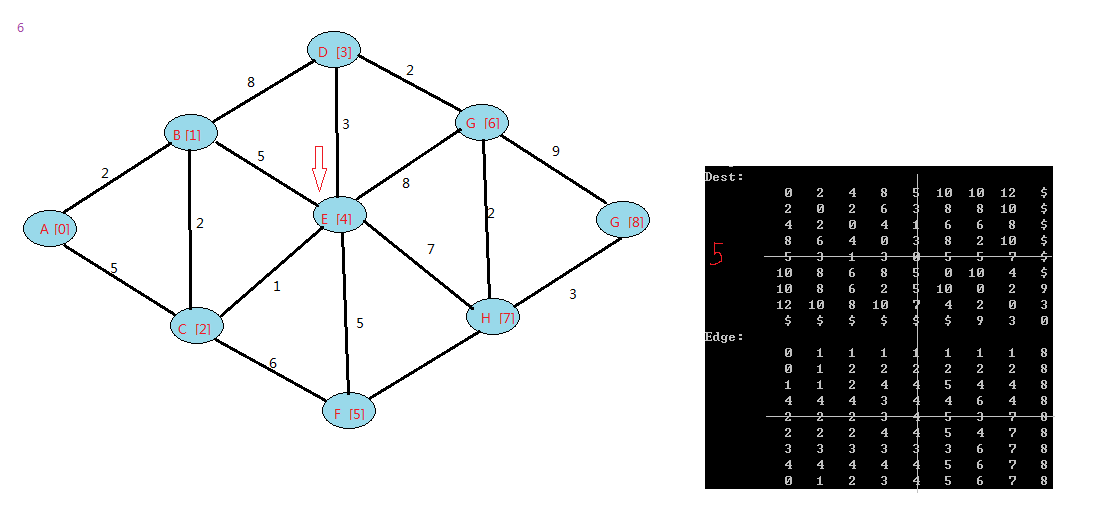
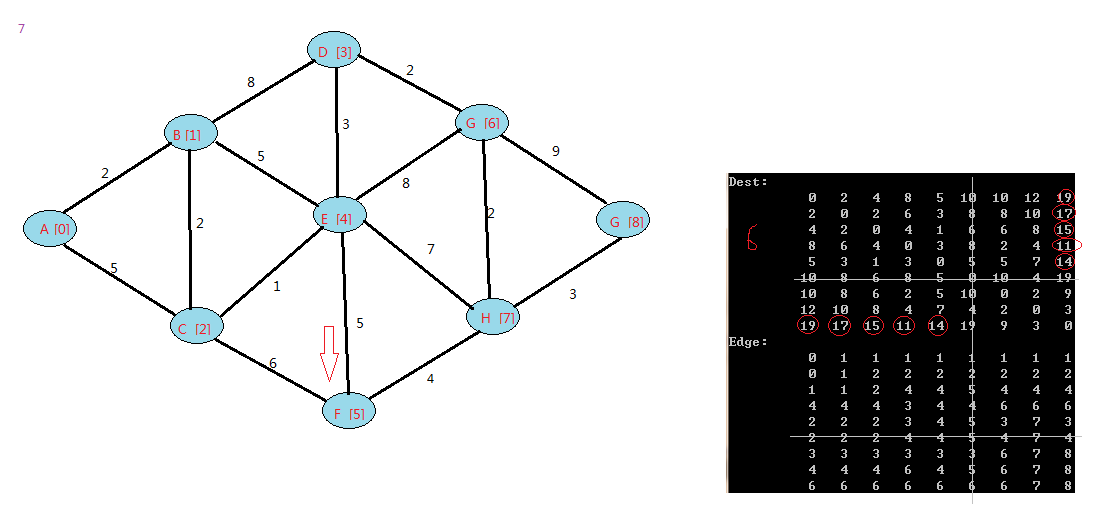
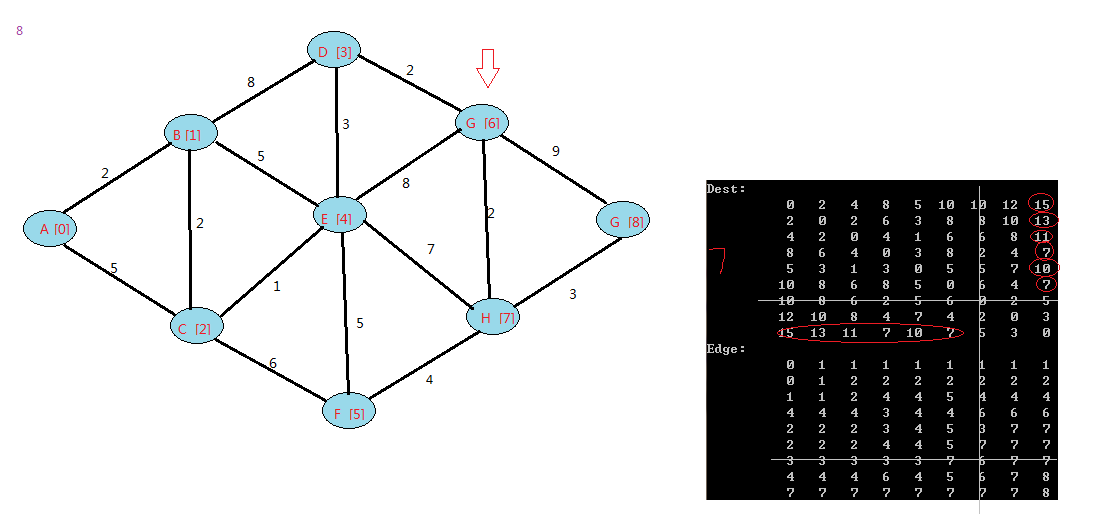
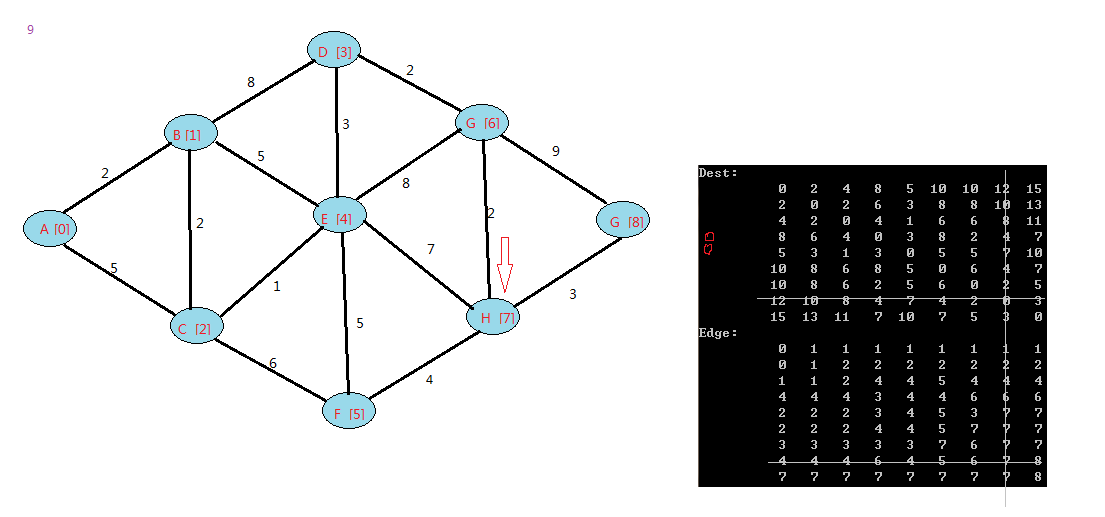
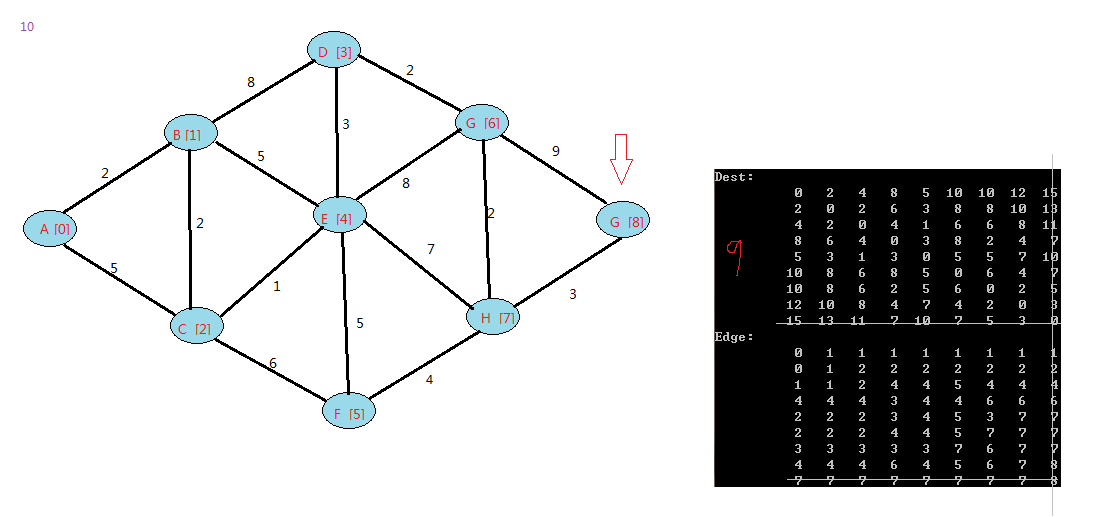
floyd算法是一个动态规划的过程，可以上网查下图中中关于它的证明。

代码：

void floyd(MGraph g,EdgeType *des,EdgeType *path)
{
    //初始化 des，path
    int i,j;

    for (i=;i<g.numVexs;i++)
    {
        for (j=;j<g.numVexs;j++)
        {
            *(des + i*MAXVEX +j) = g.Mat[i][j];
            *(path + i*MAXVEX +j) = j;
        }
    }

    int k;
    for (k=;k<g.numVexs;k++)
    {
        for (i=;i<g.numVexs;i++)
        {
            for (j=;j<g.numVexs;j++)
            {
                //printf("[%d][%d]---%d  [%d][%d]+[%d][%d]---%d\n", i,j,*(des +i*MAXVEX +j),i,k,k,j,g.Mat[i][k] + g.Mat[k][j]);
                if ( *(des +i*MAXVEX +j) > *(des +i*MAXVEX +k) + *(des + k*MAXVEX + j))
                {

                    *( des + i*MAXVEX +j ) = *(des +i*MAXVEX +k) + *(des + k*MAXVEX + j);
                    *( path + i*MAXVEX + j ) = *(path+i*MAXVEX +k);
                }
            }
        }
        if (k == )
        {
            break;
        }
    }
}

第一个for是初始化，第二个for快里面嵌入2个for循环，三个for循环完成最短路径的查找，算法很神奇。

调用后，我给出的结果是一个矩阵形式：

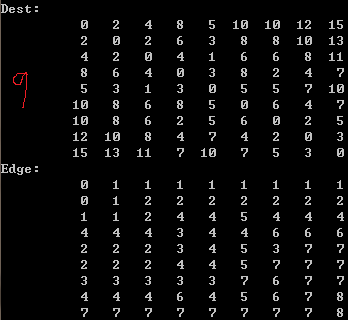
在Dest中，表示v0（A）到其他点的最短距离，和之前的Dijkstra算法对顶点A的结果一致。其他行类推。

在Edge中，由于点初始化的时候，每个点写入的是自己，这样在查看最短路径的时候，这样看

比如查找v0->v8的最小路径，查看第一行（v0）的第八行（v8）：显示是1，表示到v8点，需要经过v1，

再查看第二行（v1）到v8的值：2,，表示v1到v8需要经过v2。。。依次类推。

v0到v8的路径为：

v0->1->v2->v4->v7->v8

可以写一个代码来显示最短路径：

void prt_short_path(int vs,int ve,EdgeType *p)
{
    int x = vs;
    printf(" %c --> ",g_init_vexs[x]);
    while(x != ve)
    {
        x = *(p + MAXVEX*x + ve);
        printf(" %c --> ",g_init_vexs[x]);
    }
}

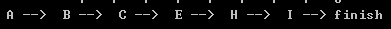
完整代码：

// grp-dijkstra.cpp : 定义控制台应用程序的入口点。
//

#include "stdafx.h"
#include <stdlib.h>
#include <string.h>

#define MAXVEX 100
#define IFY 65535

typedef char VertexType;
typedef int  EdgeType;

bool g_visited[MAXVEX];

VertexType g_init_vexs[MAXVEX] = {'A','B','C','D','E','F','G','H','I'};

EdgeType g_init_edges[MAXVEX][MAXVEX] = {
    {,,,IFY,IFY,IFY,IFY,IFY,IFY},    //'A'
    {,,,,,IFY,IFY,IFY,IFY},  //'B'
    {,,,IFY,,,IFY,IFY,IFY},//'C'
    {IFY,,IFY,,,IFY,,IFY,IFY},//'D'
    {IFY,,,,,,,,IFY},    //'E'
    {IFY,IFY,,IFY,,,IFY,,IFY},    //'F'
    {IFY,IFY,IFY,,,IFY,,,},    //'G'
    {IFY,IFY,IFY,IFY,,,,,},    //'H'
    {IFY,IFY,IFY,IFY,IFY,IFY,,,},    //'I'
};

//静态图-邻接矩阵
typedef struct {
    VertexType vexs[MAXVEX];
    EdgeType Mat[MAXVEX][MAXVEX];
    int numVexs,numEdges;
}MGraph;

//====================================================================
//打印矩阵
void prt_maxtix(EdgeType *p,int vexs)
{
    int i,j;
    for (i=;i<vexs;i++)
    {
        printf("\t");
        for (j=;j<vexs;j++)
        {
            if( (*(p + MAXVEX*i + j)) == IFY)
            {
                printf("  $ ");
            }
            else
            {
                printf(" %2d ", *(p + MAXVEX*i + j));
            }
        }
        printf("\n");
    }
}

//check the number of vextex
int getVexNum(VertexType *vexs)
{
    VertexType *pos = vexs;
    int cnt=;
    while(*pos <= 'Z' && *pos >= 'A')
    {
        cnt++;
        pos++;
    }
    return cnt;
}

bool checkMat(EdgeType *p,VertexType numvex)
{
    int i,j;
    for (i=;i<numvex;i++)
    {
        for(j=i+;j<numvex;j++)
        {
            //printf("[%d][%d] = %d\t",i,j,*(p + MAXVEX*i + j));
            //printf("[%d][%d] = %d\n",j,i,*(p + MAXVEX*j + i));
            if (*(p + MAXVEX*i + j) != *(p + MAXVEX*j +i) )
            {
                printf("ERROR:Mat[%d][%d] or Mat[%d][%d] not equal!\n",i,j,j,i);
                return false;
            }
        }
    }
    return true;
}

void init_Grp(MGraph *g,VertexType *v,EdgeType *p)
{
    int i,j;
    // init vex num
    (*g).numVexs = getVexNum(v);

    //init vexter
    for (i=;i<(*g).numVexs;i++)
    {
        (*g).vexs[i]=*v;
        v++;
    }

    //init Mat
    for (i=;i<(*g).numVexs;i++)
    {
        for (j=;j<(*g).numVexs;j++)
        {
            (*g).Mat[i][j] = *(p + MAXVEX*i + j);
        }
    }
    if(checkMat(&((*g).Mat[][]),(*g).numVexs) == false)
    {
        printf("init error!\n");
        getchar();
        exit();
    }
}

void init_path(EdgeType *p,int num)
{
    int i,j;
    for (i=;i<num;i++)
    {
        for (j=;j<num;j++)
        {
            *(p + i*MAXVEX + j) = j;
        }
    }
}

void floyd(MGraph g,EdgeType *des,EdgeType *path)
{
    //初始化 des，path
    int i,j;

    for (i=;i<g.numVexs;i++)
    {
        for (j=;j<g.numVexs;j++)
        {
            *(des + i*MAXVEX +j) = g.Mat[i][j];
            *(path + i*MAXVEX +j) = j;
        }
    }

    int k;
    for (k=;k<g.numVexs;k++)
    {
        for (i=;i<g.numVexs;i++)
        {
            for (j=;j<g.numVexs;j++)
            {
                //printf("[%d][%d]---%d  [%d][%d]+[%d][%d]---%d\n", i,j,*(des +i*MAXVEX +j),i,k,k,j,g.Mat[i][k] + g.Mat[k][j]);
                if ( *(des +i*MAXVEX +j) > *(des +i*MAXVEX +k) + *(des + k*MAXVEX + j))
                {

                    *( des + i*MAXVEX +j ) = *(des +i*MAXVEX +k) + *(des + k*MAXVEX + j);
                    *( path + i*MAXVEX + j ) = *(path+i*MAXVEX +k);
                }
            }
        }

    }
}
void prt_short_path(int vs,int ve,EdgeType *p)
{
    int x = vs;
    printf(" %c --> ",g_init_vexs[x]);
    while(x != ve)
    {
        x = *(p + MAXVEX*x + ve);
        printf(" %c --> ",g_init_vexs[x]);
    }
}
int _tmain(int argc, _TCHAR* argv[])
{
    MGraph grp;

    EdgeType edgeDest[MAXVEX][MAXVEX];
    EdgeType edgePath[MAXVEX][MAXVEX];

    int i;

    init_Grp(&grp,g_init_vexs,&g_init_edges[][]);
    prt_maxtix(&grp.Mat[][],grp.numVexs);
    printf("Floyd start!\n");
    floyd(grp,&edgeDest[][],&edgePath[][]);

    printf("Dest:\n");
    prt_maxtix(&edgeDest[][],grp.numVexs);

    printf("Edge:\n");
    prt_maxtix(&edgePath[][],grp.numVexs);

    prt_short_path(,,&edgePath[][]);
    printf("finish\n");
    getchar();
    return ;
}