POJ(有向图求LCA)

Closest Common Ancestors

Time Limit: 2000MS		Memory Limit: 10000K
Total Submissions: 18013		Accepted: 5774

Description

Write a program that takes as input a rooted tree and a list of pairs of vertices. For each pair (u,v) the program determines the closest common ancestor of u and v in the tree. The closest common ancestor of two nodes u and v is the node w that is an ancestor of both u and v and has the greatest depth in the tree. A node can be its own ancestor (for example in Figure 1 the ancestors of node 2 are 2 and 5)

Input

The data set, which is read from a the std input, starts with the tree description, in the form:

nr_of_vertices 
vertex:(nr_of_successors) successor1 successor2 ... successorn 
...
where vertices are represented as integers from 1 to n ( n <= 900 ). The tree description is followed by a list of pairs of vertices, in the form: 
nr_of_pairs 
(u v) (x y) ...

The input file contents several data sets (at least one). 
Note that white-spaces (tabs, spaces and line breaks) can be used freely in the input.

Output

For each common ancestor the program prints the ancestor and the number of pair for which it is an ancestor. The results are printed on the standard output on separate lines, in to the ascending order of the vertices, in the format: ancestor:times 
For example, for the following tree: 

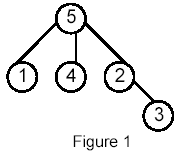
Sample Input

5
5:(3) 1 4 2
1:(0)
4:(0)
2:(1) 3
3:(0)
6
(1 5) (1 4) (4 2)
      (2 3)
(1 3) (4 3)

Sample Output

2:1
5:5
有向图求LCA，注意输入的处理。
有向图只有一个树根,利用并查集求树根。无向图中可选任意一点作树根,在dfs是比有向图多一个条件，详情见代码。

#include"cstdio"
#include"cstring"
#include"vector"
using namespace std;
const int MAXN=;
int V;
vector<int> G[MAXN];
int par[MAXN];
void prep()
{
    for(int i=;i<=MAXN;i++)
    {
        par[i]=i;
    }
}
int fnd(int x)
{
    if(par[x]==x)
        return x;
    return par[x]=fnd(par[x]);
}
void unite(int father,int son)
{
    par[son]=fnd(father);
}
int fa[MAXN],dep[MAXN];
void dfs(int u,int father,int d)
{
    fa[u]=father,dep[u]=d;
    for(int i=;i<G[u].size();i++)
         dfs(G[u][i],u,d+);//在无向图中 需要加上 if(G[u][i]!=father)
}
int lca[MAXN];
int LCA(int u,int v)
{
    while(dep[u]>dep[v])    u=fa[u];
    while(dep[v]>dep[u])    v=fa[v];
    while(u!=v)
    {
        u=fa[u];
        v=fa[v];
    }
    return u;
}
int main()
{
    while(scanf("%d",&V)!=EOF)
    {
        for(int i=;i<=V;i++)    G[i].clear();
        prep();
        memset(lca,,sizeof(lca));
        for(int i=;i<V;i++)
        {
            int u,t;
            scanf("%d:(%d)",&u,&t);
            while(t--)
            {
                int v;
                scanf("%d",&v);
                G[u].push_back(v);
                unite(u,v);
            }
        }
        int root=fnd();
        dfs(root,-,);
        int Q;
        scanf("%d",&Q);
        while(true)
        {
            char ch=getchar();
            if(ch=='(')
            {
                int u,v;
                scanf("%d %d",&u,&v);
                int a=LCA(u,v);
                lca[a]++;
                Q--;
                getchar();//不能丢,有开就有闭
            }
            if(Q==)    break;
        }
        for(int i=;i<=V;i++)
        {
            if(lca[i]!=)    printf("%d:%d\n",i,lca[i]);
        }
    }
    return ;
}

tarjan+并查集离线算法

#include"cstdio"
#include"cstring"
#include"vector"
using namespace std;
const int MAXN=;
int V;
vector<int> G[MAXN];
int que[MAXN][MAXN];
int vis[MAXN];
int par[MAXN];
int cnt[MAXN];
void prep()
{
    for(int i=;i<=MAXN;i++)
        par[i]=i;
}
int fnd(int x)
{
    if(par[x]==x)
        return x;
    return par[x]=fnd(par[x]);
}
void unite(int father,int son)
{
    par[son]=fnd(father);
}
void dfs(int u)
{
    for(int i=;i<=V;i++)
        if(vis[i]&&que[u][i])
        {
            int fa=fnd(i);//fa 为u与i的LCA
            cnt[fa]+=que[u][i];
        }
    vis[u]=;
    for(int i=;i<G[u].size();i++)
    {
        int v=G[u][i];
        dfs(v);
        unite(u,v);
    }
}
int indeg[MAXN];
int main()
{
    while(scanf("%d",&V)!=EOF)
    {
        prep();
        for(int i=;i<=V;i++)    G[i].clear();
        memset(que,,sizeof(que));
        memset(vis,,sizeof(vis));
        memset(cnt,,sizeof(cnt));
        memset(indeg,,sizeof(indeg));
        for(int i=;i<V;i++)
        {
            int u,t;
            scanf("%d:(%d)",&u,&t);
            while(t--)
            {
                int v;
                scanf("%d",&v);
                G[u].push_back(v);
                indeg[v]++;
            }
        }
        int Q;
        scanf("%d",&Q);
        while(Q--)
        {
            int u,v;
            scanf(" (%d %d)",&u,&v);
            que[u][v]++;
            que[v][u]++;
        }
        for(int i=;i<=V;i++)
            if(!indeg[i])//入度为0的点为根节点
            {
                dfs(i);
                break;
            }
        for(int i=;i<=V;i++)
            if(cnt[i]!=)    printf("%d:%d\n",i,cnt[i]);
    }
    return ;
}