BZOJ4555 [Tjoi2016&Heoi2016]求和 【第二类斯特林数 + NTT】

题目

在2016年，佳媛姐姐刚刚学习了第二类斯特林数，非常开心。

现在他想计算这样一个函数的值:



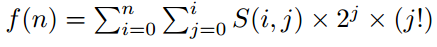
S(i, j)表示第二类斯特林数，递推公式为:

S(i, j) = j ∗ S(i − 1, j) + S(i − 1, j − 1), 1 <= j <= i − 1。

边界条件为：S(i, i) = 1(0 <= i), S(i, 0) = 0(1 <= i)

你能帮帮他吗?

输入格式

输入只有一个正整数

输出格式

输出f(n)。由于结果会很大，输出f(n)对998244353(7 × 17 × 223 + 1)取模的结果即可。1 ≤ n ≤ 100000

输入样例

3

输出样例

87

题解

当第二类斯特林数\(j > i\)时值为\(0\)

所以我们实际求：

\[\begin{aligned}
ans &= \sum\limits_{i = 0}^{n} \sum\limits_{j = 0}^{n} \begin{Bmatrix} i \\ j \end{Bmatrix} 2^{j}j! \\
&= \sum\limits_{i = 0}^{n} \sum\limits_{j = 0}^{n} 2^{j}j! \frac{1}{j!} \sum\limits_{k = 0}^{j} (-1)^{k}{j \choose k}(j - k)^{i} \\
&= \sum\limits_{i = 0}^{n} \sum\limits_{j = 0}^{n} 2^{j}j! \sum\limits_{k = 0}^{j} \frac{(-1)^{k}}{k!} * \frac{(j - k)^{i}}{(j - k)!} \\
&= \sum\limits_{j = 0}^{n} 2^{j}j! \sum\limits_{k = 0}^{j} \frac{(-1)^{k}}{k!} * \frac{\sum\limits_{i = 0}^{n} (j - k)^{i}}{(j - k)!} \\
\end{aligned}
\]

NTT即可

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
#define LL long long int
#define Redge(u) for (int k = h[u],to; k; k = ed[k].nxt)
#define REP(i,n) for (int i = 1; i <= (n); i++)
#define BUG(s,n) for (int i = 1; i <= (n); i++) cout<<s[i]<<' '; puts("");
using namespace std;
const int maxn = 400005,maxm = 100005,INF = 1000000000;
inline int read(){
	int out = 0,flag = 1; char c = getchar();
	while (c < 48 || c > 57){if (c == '-') flag = -1; c = getchar();}
	while (c >= 48 && c <= 57){out = (out << 3) + (out << 1) + c - 48; c = getchar();}
	return out * flag;
}
const int G = 3,P = 998244353;
int fac[maxn],fv[maxn],inv[maxn],bin[maxn],g[maxn];
int L,R[maxn],A[maxn],B[maxn],n,m,N;
inline int qpow(int a,int b){
	int ans = 1;
	for (; b; b >>= 1,a = 1ll * a * a % P)
		if (b & 1) ans = 1ll * ans * a % P;
	return ans;
}
void init(){
	fac[0] = fac[1] = inv[0] = inv[1] = fv[0] = fv[1] = 1;
	bin[0] = 1; bin[1] = 2;
	g[0] = 1; g[1] = N + 1;
	for (int i = 2; i <= N; i++){
		fac[i] = 1ll * fac[i - 1] * i % P;
		inv[i] = 1ll * (P - P / i) * inv[P % i] % P;
		fv[i] = 1ll * fv[i - 1] * inv[i] % P;
		bin[i] = 2ll * bin[i - 1] % P;
		g[i] = 1ll * (1ll * qpow(i,N + 1) - 1 + P) % P * inv[i - 1] % P;
	}
}
void NTT(int* a,int f){
	for (int i = 0; i < n; i++) if (i < R[i]) swap(a[i],a[R[i]]);
	for (int i = 1; i < n; i <<= 1){
		int gn = qpow(G,(P - 1) / (i << 1));
		for (int j = 0; j < n; j += (i << 1)){
			int g = 1,x,y;
			for (int k = 0; k < i; k++,g = 1ll * g * gn % P){
				x = a[j + k]; y = 1ll * g * a[j + k + i] % P;
				a[j + k] = (x + y) % P; a[j + k + i] = ((x - y) % P + P) % P;
			}
		}
	}
	if (f == 1) return;
	int nv = qpow(n,P - 2); reverse(a + 1,a + n);
	for (int i = 0; i < n; i++) a[i] = 1ll * a[i] * nv % P;
}
int main(){
	N = read();
	init();
	for (int i = 0; i <= N; i++){
		A[i] = ((i & 1) ? -1ll : 1ll) * fv[i] % P;
		B[i] = 1ll * g[i] * fv[i] % P;
	}
	m = N + N; L = 0;
	for (n = 1; n <= m; n <<= 1) L++;
	for (int i = 1; i < n; i++) R[i] = (R[i >> 1] >> 1) | ((i & 1) << (L - 1));
	NTT(A,1); NTT(B,1);
	for (int i = 0; i < n; i++) A[i] = 1ll * A[i] % P * B[i] % P;
	NTT(A,-1);
	int ans = 0;
	for (int i = 0; i <= N; i++)
		ans = (ans + 1ll * bin[i] * fac[i] % P * A[i] % P) % P;
	printf("%d\n",(ans % P + P) % P);
	return 0;
}