集训Day5

生活还得继续

bzoj3771

题面让我笑了很长时间

给出 n个物品，价值为别为Xi且各不相同，现在可以取1个、2个或3个，问每种价值和有几种情况？

*顺序不同算一种

很傻逼的一个母函数+容斥，用A(x)表示每种取一个的母函数，B(x)表示每种取两个，C(x)表示每种取三个

显然所以对于每种物品价值Xi,A[xi]++,B[2*xi]++,C[3*xi]++

然后就是

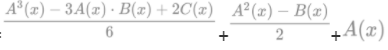
然后就是FFT啦

bzoj1101

对于给定的整数a,b和d，有多少正整数对x,y，满足x<=a，y<=b，并且gcd(x,y)=d

第一行包含一个正整数n，表示一共有n组询问。（1<=n<= 50000）接下来n行，每行表示一个询问，每行三个
正整数，分别为a,b,d。（1<=d<=a,b<=50000）

波兰科技这么发达的吗

这么早的一道莫反题。。。

草稿纸太乱 贴一个黄学长的吧

bzoj4571

看到xor上一个Trie树

然后每一步转移其实是用主席树查找一个区间里的数

同样是按照数位一位一位的贪心，因为加了一个x，所以我们考虑对于所有的ai+x与b的按位异或。

假设我们已经处理到b的第i位（转换成二进制），假设是1（0同理），

那么我们只需要查找是否存在aj+x使得其二进制第i位数字是0，显然我们已经处理了前i-1位了，设当前结果是ans，那么我们需要查找的数的大小就是在区间[ans-x,ans+(1<<i)-1-x]，手算一下就知道这个区间里的数字的第i位加了x后就都是0，

那么现在我们就是要在a[1]...a[n]中找出是否存在于[ans-x,ans+(1<<i)-1-x]的数字，两个区间范围限制，用主席树模板一套就好了。