乐在其中设计模式(C#) - 原型模式(Prototype Pattern)

原文:乐在其中设计模式(C#) - 原型模式(Prototype Pattern)

[索引页][源码下载]

乐在其中设计模式(C#) - 原型模式(Prototype Pattern)

作者：webabcd





介绍

用原型实例指定创建对象的种类，并且通过拷贝这个原型来创建新的对象。





示例

有一个Message实体类，现在要克隆它。







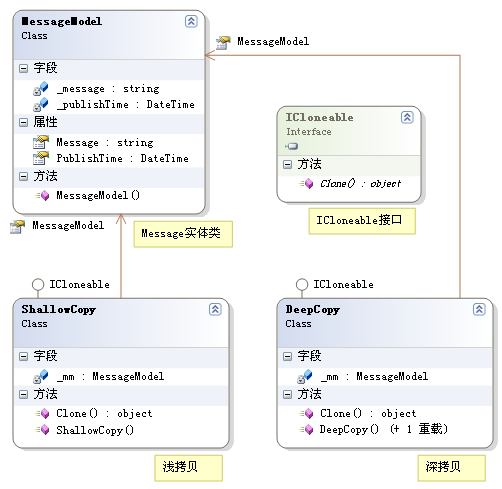
MessageModel

using System;

using System.Collections.Generic;

using System.Text;



namespace Pattern.Prototype

{

    /**//// <summary>

    /// Message实体类

    /// </summary>

    public class MessageModel

    {

        /**//// <summary>

        /// 构造函数

        /// </summary>

        /// <param name="msg">Message内容</param>

        /// <param name="pt">Message发布时间</param>

        public MessageModel(string msg, DateTime pt)

        {

            this._message = msg;

            this._publishTime = pt;

        }



        private string _message;

        /**//// <summary>

        /// Message内容

        /// </summary>

        public string Message

        {

            get { return _message; }

            set { _message = value; }

        }



        private DateTime _publishTime;

        /**//// <summary>

        /// Message发布时间

        /// </summary>

        public DateTime PublishTime

        {

            get { return _publishTime; }

            set { _publishTime = value; }

        }

    }

}

ShallowCopy

using System;

using System.Collections.Generic;

using System.Text;



namespace Pattern.Prototype

{

    /**//// <summary>

    /// 浅拷贝

    /// </summary>

    public class ShallowCopy : ICloneable

    {

        /**//// <summary>

        /// 构造函数

        /// </summary>

        public ShallowCopy()

        {

            

        }



        /**//// <summary>

        /// 实现ICloneable的Clone()方法

        /// </summary>

        /// <returns></returns>

        public Object Clone()

        {

            return this.MemberwiseClone();

        }



        private MessageModel _mm;

        /**//// <summary>

        /// Message实体对象

        /// </summary>

        public MessageModel MessageModel

        {

            get { return _mm; }

            set { _mm = value; }

        }

    }

}

DeepCopy

using System;

using System.Collections.Generic;

using System.Text;



namespace Pattern.Prototype

{

    /**//// <summary>

    /// 深拷贝

    /// </summary>

    public class DeepCopy : ICloneable

    {

        /**//// <summary>

        /// 构造函数

        /// </summary>

        public DeepCopy()

        {

            

        }



        /**//// <summary>

        /// 构造函数

        /// </summary>

        /// <param name="mm">Message实体对象</param>

        public DeepCopy(MessageModel mm)

        {

            _mm = mm;

        }



        /**//// <summary>

        /// 实现ICloneable的Clone()方法

        /// </summary>

        /// <returns></returns>

        public Object Clone()

        {

            return new DeepCopy(new MessageModel(_mm.Message, _mm.PublishTime));

        }



        private MessageModel _mm;

        /**//// <summary>

        /// Message实体对象

        /// </summary>

        public MessageModel MessageModel

        {

            get { return _mm; }

            set { _mm = value; }

        }

    }

}

client

using System;

using System.Data;

using System.Configuration;

using System.Collections;

using System.Web;

using System.Web.Security;

using System.Web.UI;

using System.Web.UI.WebControls;

using System.Web.UI.WebControls.WebParts;

using System.Web.UI.HtmlControls;



using Pattern.Prototype;



public partial class Prototype : System.Web.UI.Page

{

    protected void Page_Load(object sender, EventArgs e)

    {

        Response.Write("ShallowCopy演示如下：<br />");

        ShowShallowCopy();



        Response.Write("DeepCopy演示如下：<br />");

        ShowDeepCopy();    

    }



    private void ShowShallowCopy()

    {

        ShallowCopy sc = new ShallowCopy();

        sc.MessageModel = new MessageModel("ShallowCopy", DateTime.Now);



        ShallowCopy sc2 = (ShallowCopy)sc.Clone();



        Response.Write(sc.MessageModel.Message);

        Response.Write("<br />");

        Response.Write(sc2.MessageModel.Message);

        Response.Write("<br />");



        sc.MessageModel.Message = "ShallowCopyShallowCopy";



        Response.Write(sc.MessageModel.Message);

        Response.Write("<br />");

        Response.Write(sc2.MessageModel.Message);

        Response.Write("<br />");

    }



    private void ShowDeepCopy()

    {

        DeepCopy sc = new DeepCopy();

        sc.MessageModel = new MessageModel("DeepCopy", DateTime.Now);



        DeepCopy sc2 = (DeepCopy)sc.Clone();



        Response.Write(sc.MessageModel.Message);

        Response.Write("<br />");

        Response.Write(sc2.MessageModel.Message);

        Response.Write("<br />");



        sc.MessageModel.Message = "DeepCopyDeepCopy";



        Response.Write(sc.MessageModel.Message);

        Response.Write("<br />");

        Response.Write(sc2.MessageModel.Message);

        Response.Write("<br />");

    }

}

运行结果

ShallowCopy演示如下：

ShallowCopy

ShallowCopy

ShallowCopyShallowCopy

ShallowCopyShallowCopy

DeepCopy演示如下：

DeepCopy

DeepCopy

DeepCopyDeepCopy

DeepCopy





参考

http://www.dofactory.com/Patterns/PatternPrototype.aspx





OK

[源码下载]