codeforces#1152D. Neko and Aki's Prank（dp）

题目链接：

https://codeforces.com/contest/1152/problem/D

题意：

给出一个$n$，然后在匹配树上染色边，每个结点的所有相邻边只能被染色一次。

问，这颗树上最多染色多少边。

匹配树，就是深度为$2n$的树，每个节点都是一个字符串，只包含$(，)$，以长度为$2n$的合法匹配字符串作为叶子。每个节点的父亲是比自身长度小一的节点。

数据范围：

$1 \le n \le 1000$

分析：

在百度找了很久都没找到满意的题解，于是看了cf给的官方题解。虽然是全英文，但我居然看明白了！

实现起来不同，但是思路是一样的。

贪心的方法是，先染色叶子和叶子节点的父亲，并且去除它们，再染色叶子和叶子节点的父亲。

定义不平衡度，$($的数量减$)$的数量。

长度为x，不平衡度为y的子树染色方案数相同

例如这些节点$((()),()()(,(())($的子树，染色方案数相同

选择定义$dp[x][y]$，根节点长度为$x$，不平衡度为$y$，的子树的染色方案数

转移方程为

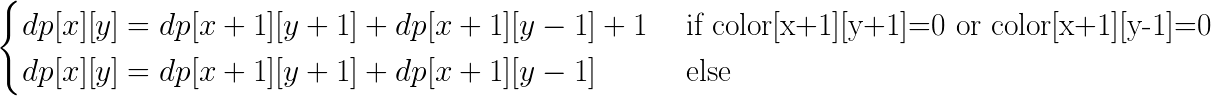
$ans=dp[0][0]$

ac代码：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=1e3+10;
const int maxm=1e7+10;
const int mod=1e9+7;
ll dp[2*maxn][2*maxn];
bool color[2*maxn][2*maxn];
int main()
{
    int n;
    scanf("%d",&n);
    for(int i=2*n-1;i>=0;i--)
    {
        for(int j=0;j<=2*n-i;j++)
        {
            int flag=0;
            if(j-1>=0)
            {
                dp[i][j]=(dp[i][j]+dp[i+1][j-1])%mod;
                if(color[i+1][j-1]==0)flag=1;
            }
            if(j+1<=2*n-i-1)
            {
                dp[i][j]=(dp[i][j]+dp[i+1][j+1])%mod;
                if(color[i+1][j+1]==0)flag=1;
            }
            if(flag)color[i][j]=1,dp[i][j]=(dp[i][j]+1)%mod;
        }
    }
    printf("%d\n",dp[0][0]);
    return 0;
}