CodeForces 918D MADMAX(博弈+记忆化搜索)

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

As we all know, Max is the best video game player among her friends. Her friends were so jealous of hers, that they created an actual game just to prove that she's not the best at games. The game is played on a directed acyclic graph (a DAG) with n vertices and m edges. There's a character written on each edge, a lowercase English letter.

Max and Lucas are playing the game. Max goes first, then Lucas, then Max again and so on. Each player has a marble, initially located at some vertex. Each player in his/her turn should move his/her marble along some edge (a player can move the marble from vertex v to vertex u if there's an outgoing edge from v to u). If the player moves his/her marble from vertex v to vertex u, the "character" of that round is the character written on the edge from v to u. There's one additional rule; the ASCII code of character of round i should be greater than or equal to the ASCII code of character of round i - 1 (for i > 1). The rounds are numbered for both players together, i. e. Max goes in odd numbers, Lucas goes in even numbers. The player that can't make a move loses the game. The marbles may be at the same vertex at the same time.

Since the game could take a while and Lucas and Max have to focus on finding Dart, they don't have time to play. So they asked you, if they both play optimally, who wins the game?

You have to determine the winner of the game for all initial positions of the marbles.

Input

The first line of input contains two integers n and m (2 ≤ n ≤ 100, ).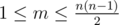

The next m lines contain the edges. Each line contains two integers v, u and a lowercase English letter c, meaning there's an edge from vto u written c on it (1 ≤ v, u ≤ n, v ≠ u). There's at most one edge between any pair of vertices. It is guaranteed that the graph is acyclic.

Output

Print n lines, a string of length n in each one. The j-th character in i-th line should be 'A' if Max will win the game in case her marble is initially at vertex i and Lucas's marble is initially at vertex j, and 'B' otherwise.

Examples

input

4 4
1 2 b
1 3 a
2 4 c
3 4 b

output

BAAA
ABAA
BBBA
BBBB

input

5 8
5 3 h
1 2 c
3 1 c
3 2 r
5 1 r
4 3 z
5 4 r
5 2 h

output

BABBB
BBBBB
AABBB
AAABA
AAAAB
题意：给出一个有向无环图，每条边的边权都是小写字母，两个人分别从i点和j点出发，每个人能走的边边权必须大于等于上一个人走的边权，如果一个人无路可走，他就输了。
打印i=1~n，j=1~n的胜负表。

题解：GG我又双叒叕被题意杀了，写了个bfs结果呵呵
第一次接触到博弈dp
dp[i][j][v]表示先手在i，后手在j，上一条边走的边权为v的胜负情况
0表示后手必胜，1表示先手必胜
开始考虑转移
假设u点是与i点相连，边权为c
则只要有满足状态dp[j][u][c]=0的v存在，那么dp[i][j][v]=1（对手必败，则我们必胜）否则dp[i][j][v]=0
然后记忆化搜索一下，就可以了

代码如下:

#include<cstdio>
#include<vector>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;

vector< pair<int,int> > g[];
int n,m;
int f[][][];

int dfs(int a,int b,int v)
{
    if(f[a][b][v]!=-)
    {
        return f[a][b][v];
    }
    f[a][b][v]=;
    for(int i=;i<g[a].size();i++)
    {
        int y=g[a][i].first;
        int w=g[a][i].second;
        if(w>=v)
        {
            if(!dfs(b,y,w))
            {
                f[a][b][v]=;
                break;
            }
        }
    }
    return f[a][b][v];
}

int main()
{
    memset(f,-,sizeof(f));
    scanf("%d%d",&n,&m);
    for(int i=;i<=m;i++)
    {
        char c;
        int from,to;
        scanf("\n%d %d %c",&from,&to,&c);
        g[from].push_back(make_pair(to,c-'a'));
    }
    for(int i=;i<=n;i++)
    {
        for(int j=;j<=n;j++)
        {
            if(dfs(i,j,))
            {
                printf("A");
            }
            else
            {
                printf("B");
            }
        }
        printf("\n");
    }
}