声明：本文参考《大数据：Spark mlib(三) GradientDescent梯度下降算法之Spark实现》

1. 什么是梯度下降？

梯度下降法（英语：Gradient descent）是一个一阶最优化算法，通常也称为最速下降法。要使用梯度下降法找到一个函数的局部极小值，必须向函数上当前点对应梯度（或者是近似梯度）的反方向的规定步长距离点进行迭代搜索。

先来看两个函数：

1. 拟合函数：为参数向量，h(θ)就是通过参数向量计算的值，n为参数的总个数，j代表的是一条记录里的一个参数

2. 损失函数：

m为训练的集合数，i代表的是一条记录，hθ(xi)代表的是第i条的h(θ)

在监督学习模型中，需要对原始的模型构建损失函数J(θ), 接着就是最小化损失函数，用以求的最优参数θ

对损失函数θ进行求偏导，获取每个θ的梯度

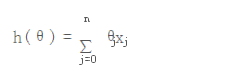
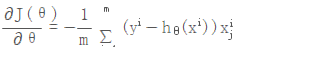
2. 梯度下降的几种方式

2.1 批量梯度下降（BGD）

在前面的方式，我们采样部分数据，就称为批量梯度下降

在公式：

中我们会发现随着计算θ的梯度下降，需要计算所有的采样数据m，计算量会比较大。

2.2 随机梯度下降 (SGD)

在上面2.1的批量梯度下降，采样的是批量数据，那么随机采样一个数据，进行θ梯度下降，就被称为随机梯度下降。

损失函数：

那么单样本的损失函数：m=1 的情况：

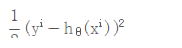
对单样本的损失函数进行求偏导，计算梯度下降

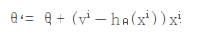
为了控制梯度下降的速度，引入步长

3. Spark 实现的梯度下降

spark实现在mlib库下org.apache.spark.mllib.optimization.GradientDescent类中

3.1 随机梯度？

看函数名字叫做SGD，会以为是随机梯度下降，实际上Spark里实现的是随机批量的梯度下降

我们去看梯度下降的批量算法公式：

这个公式可以拆分成两部分

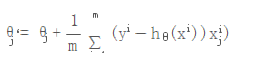
计算数据的梯度
根据梯度计算新的权重

3.2 计算梯度

在前面的章节里描述过随机和批量的主要区别就是在计算梯度上，随机采样只是随机采用单一样本，而批量采样如果采样所有数据，涉及到采样的样本、计算量大的问题，Spark采用了择中的策略，随机采样部分数据

先随机采样部分数据

data.sample(false, miniBatchFraction, 42 + i)

对部分数据样本进行聚合计算

treeAggregate((BDV.zeros[Double](n), 0.0, 0L))(

          seqOp = (c, v) => {

            // c: (grad, loss, count), v: (label, features)

            val l = gradient.compute(v._2, v._1, bcWeights.value, Vectors.fromBreeze(c._1))

            (c._1, c._2 + l, c._3 + 1)

          },

          combOp = (c1, c2) => {

            // c: (grad, loss, count)

            (c1._1 += c2._1, c1._2 + c2._2, c1._3 + c2._3)

          })

使用treeAggregate，而没有使用Aggregate，是因为treeAggregate比aggregate更高效，combOp会在executor上执行

在聚合计算的seqOp里我们看到了gradient.compute来计算梯度

3.2.1 Spark 提供的计算梯度的方式

LeastSquaresGradient 梯度，主要用于线型回归
HingeGradient 梯度，用于SVM分类
LogisticGradient 梯度，用于逻辑回归

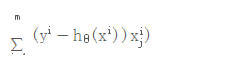
前面章节里描述的就是基于线性回归模型的计算梯度的方式，也就是如下公式：

3.3 跟新权重theta θ

在梯度下降计算中，计算新的theta（也叫权重的更新），更新的算法由你采用的模型来决定

val update = updater.compute(

          weights, Vectors.fromBreeze(gradientSum / miniBatchSize.toDouble),

          stepSize, i, regParam)

目前Spark默认提供了3种算法跟新theta

SimpleUpdater
L1Updater
SquaredL2Updater

3.3.1 SimpleUpdater

以SimpleUpdater来说：

SimpleUpdater extends Updater {

  override def compute(

      weightsOld: Vector,

      gradient: Vector,

      stepSize: Double,

      iter: Int,

      regParam: Double): (Vector, Double) = {

    val thisIterStepSize = stepSize / math.sqrt(iter)

    val brzWeights: BV[Double] = weightsOld.asBreeze.toDenseVector

    brzAxpy(-thisIterStepSize, gradient.asBreeze, brzWeights)  

    (Vectors.fromBreeze(brzWeights), 0)

  }

}

也就是上面提到的公式：

相对来说simpleupdater算法比较简单，在这里没有使用正则参数regParam，只是使用了每个迭代的步长作为相同的因子，计算每一个theta，也就是权重。

迭代的步长=总步长/math.sqrt(迭代的次数)

3.3.2 其它的正则参数化算法

L1Updater：正则化算法

和SimpleUpdater一样更新权重
将正则化参数乘以迭代步长的到比较参数：shrinkage
如果权重大于shrinkage，设置权重-shrinkage
如果权重小于-shrinkage，设置权重+shrinkage
其它的，设置权重为0

SquaredL2Updater：正则化算法

w' = w - thisIterStepSize * (gradient + regParam * w)

和SimpleUpdater比较，补偿了regParam*w ,这也是逻辑回归所采用的梯度下降算法的更新算法

4. 梯度下降收敛条件

如何判定梯度下降权重值收敛不在需要计算，通常会有两个约束条件

迭代次数，当达到一定的迭代次数后，权重的值会被收敛到极值点，并且不会受到次数的影响
筏值：当两次迭代的权重之间的差小于指定的筏值的时候，就认为已经收敛

在Spark里使用了L2范数来比较筏值

private def isConverged(

    previousWeights: Vector,

    currentWeights: Vector,

    convergenceTol: Double): Boolean = {

  // To compare with convergence tolerance.

  val previousBDV = previousWeights.asBreeze.toDenseVector

  val currentBDV = currentWeights.asBreeze.toDenseVector  

  // This represents the difference of updated weights in the iteration.

  val solutionVecDiff: Double = norm(previousBDV - currentBDV)  

  solutionVecDiff < convergenceTol * Math.max(norm(currentBDV), 1.0)

}

当前后权重的差的L2，小于筏值*当前权重的L2和1的最大值，就认为下降结束。

5. Spark实现梯度下降的实现示例：

import org.apache.spark.sql.SparkSession

import org.apache.spark.{SparkConf}

import org.apache.spark.mllib.linalg.{Vectors}

import org.apache.spark.mllib.optimization._

object SGDExample {

  def main(args: Array[String]): Unit = {

    val conf = new SparkConf()

    conf.set("spark.sql.broadcastTimeout", "10000")

    conf.set("fs.defaultFS", "hdfs://abccluster")

    val spark = SparkSession.builder().appName("hz_mlib").config(conf).enableHiveSupport().getOrCreate()

    /**

      * 这里以简单的y=3*x+1为例来简单使用一下

      * 测试数据就随意

      * 1 0 1

      * 7 2 1

      * 10 3 1

      * 4 1 1

      * 19 6 1

      **/

    val list = List[scala.Tuple2[scala.Double, org.apache.spark.mllib.linalg.Vector]](

      Tuple2(1d, Vectors.dense(0.0d, 1d)),

      Tuple2(7d, Vectors.dense(2.0d, 1d)),

      Tuple2(10d, Vectors.dense(3.0d, 1d)),

      Tuple2(4d, Vectors.dense(1.0d, 1d)),

      Tuple2(19d, Vectors.dense(6.0d, 1d))

    )

    val data: org.apache.spark.rdd.RDD[scala.Tuple2[scala.Double, org.apache.spark.mllib.linalg.Vector]] = spark.sparkContext.parallelize(list)

    /**

      * 而具体的实现梯度有

      * LogisticGradient

      * LeastSquaresGradient

      * HingeGradient

      * 对于更新也是三种实现

      * SimpleUpdater

      * L1Updater

      * SquaredL2Updater

      **/

    var gradient = new LeastSquaresGradient()

    var updater = new L1Updater()

    /**

      * GradientDescent parameters default initialize values:

      * private var stepSize: Double = 1.0

      * private var numIterations: Int = 100

      * private var regParam: Double = 0.0

      * private var miniBatchFraction: Double = 1.0

      * private var convergenceTol: Double = 0.001

      */

    var stepSize = 1.0

    var numIterations = 100

    var regParam: Double = 0.0

    var miniBatchFraction = 1.0

    var initialWeights: org.apache.spark.mllib.linalg.Vector = Vectors.dense(0d, 0d)

    var convergenceTol = 0.001

    val (weights, _) = GradientDescent.runMiniBatchSGD(

      data: org.apache.spark.rdd.RDD[scala.Tuple2[scala.Double, org.apache.spark.mllib.linalg.Vector]],

      gradient: org.apache.spark.mllib.optimization.Gradient,

      updater: org.apache.spark.mllib.optimization.Updater,

      stepSize: scala.Double,

      numIterations: scala.Int,

      regParam: scala.Double,

      miniBatchFraction: scala.Double,

      initialWeights: org.apache.spark.mllib.linalg.Vector,

      convergenceTol: scala.Double)

    println(weights)

    spark.stop()

  }

}

输出测试结果：

scala> import org.apache.spark.mllib.linalg.{Vectors}

import org.apache.spark.mllib.linalg.Vectors

scala> import org.apache.spark.mllib.optimization._

import org.apache.spark.mllib.optimization._

scala>  /**

     |       * 这里以简单的y=3*x+1为例来简单使用一下

     |       * 测试数据就随意

     |       * 1 0 1

     |       * 7 2 1

     |       * 10 3 1

     |       * 4 1 1

     |       * 19 6 1

     |       **/

     |     val list = List[scala.Tuple2[scala.Double, org.apache.spark.mllib.linalg.Vector]](

     |       Tuple2(1d, Vectors.dense(0.0d, 1d)),

     |       Tuple2(7d, Vectors.dense(2.0d, 1d)),

     |       Tuple2(10d, Vectors.dense(3.0d, 1d)),

     |       Tuple2(4d, Vectors.dense(1.0d, 1d)),

     |       Tuple2(19d, Vectors.dense(6.0d, 1d))

     |     )

list: List[(Double, org.apache.spark.mllib.linalg.Vector)] = List((1.0,[0.0,1.0]), (7.0,[2.0,1.0]), (10.0,[3.0,1.0]), (4.0,[1.0,1.0]), (19.0,[6.0,1.0]))

scala> 

scala>     val data: org.apache.spark.rdd.RDD[scala.Tuple2[scala.Double, org.apache.spark.mllib.linalg.Vector]] = spark.sparkContext.parallelize(list)

data: org.apache.spark.rdd.RDD[(Double, org.apache.spark.mllib.linalg.Vector)] = ParallelCollectionRDD[11460] at parallelize at <console>:37

scala> 

scala>     /**

     |       * 而具体的实现梯度有

     |       * LogisticGradient

     |       * LeastSquaresGradient

     |       * HingeGradient

     |       * 对于更新也是三种实现

     |       * SimpleUpdater

     |       * L1Updater

     |       * SquaredL2Updater

     |       **/

     |     var gradient = new LeastSquaresGradient()

gradient: org.apache.spark.mllib.optimization.LeastSquaresGradient = org.apache.spark.mllib.optimization.LeastSquaresGradient@7adb7d5b

scala>     var updater = new L1Updater()

updater: org.apache.spark.mllib.optimization.L1Updater = org.apache.spark.mllib.optimization.L1Updater@33e6a825

scala> 

scala>     /**

     |       * GradientDescent parameters default initialize values:

     |       * private var stepSize: Double = 1.0

     |       * private var numIterations: Int = 100

     |       * private var regParam: Double = 0.0

     |       * private var miniBatchFraction: Double = 1.0

     |       * private var convergenceTol: Double = 0.001

     |       */

     |     var stepSize = 1.0

stepSize: Double = 1.0

scala>     var numIterations = 100

numIterations: Int = 100

scala>     var regParam: Double = 0.0

regParam: Double = 0.0

scala>     var miniBatchFraction = 1.0

miniBatchFraction: Double = 1.0

scala>     var initialWeights: org.apache.spark.mllib.linalg.Vector = Vectors.dense(0d, 0d)

initialWeights: org.apache.spark.mllib.linalg.Vector = [0.0,0.0]

scala>     var convergenceTol = 0.001

convergenceTol: Double = 0.001

scala>     val (weights, _) = GradientDescent.runMiniBatchSGD(

     |       data: org.apache.spark.rdd.RDD[scala.Tuple2[scala.Double, org.apache.spark.mllib.linalg.Vector]],

     |       gradient: org.apache.spark.mllib.optimization.Gradient,

     |       updater: org.apache.spark.mllib.optimization.Updater,

     |       stepSize: scala.Double,

     |       numIterations: scala.Int,

     |       regParam: scala.Double,

     |       miniBatchFraction: scala.Double,

     |       initialWeights: org.apache.spark.mllib.linalg.Vector,

     |       convergenceTol: scala.Double)

weights: org.apache.spark.mllib.linalg.Vector = [3.000248212261404,0.9997330919125574]

scala> 

scala>     println(weights)

[3.000248212261404,0.9997330919125574]

样例实现：参考《夜明的孤行灯 -》Spark中的梯度下降 -》 https://www.huangyunkun.com/2015/05/27/spark-gradient-descent/#comment-9317》

Spark MLib：梯度下降算法实现的更多相关文章

Spark MLib完整基础入门教程
Spark MLib 在Spark下进行机器学习,必然无法离开其提供的MLlib框架,所以接下来我们将以本框架为基础进行实际的讲解.首先我们需要了解其中最基本的结构类型,即转换器.估计器.评估器和流水 ...
梯度下降算法的一点认识（Ng第一课）
昨天开始看Ng教授的机器学习课,发现果然是不错的课程,一口气看到第二课. 第一课没有什么新知识,就是机器学习的概况吧. 第二课出现了一些听不太懂的概念.其实这堂课主要就讲了一个算法,梯度下降算法. ...
ng机器学习视频笔记（二） ——梯度下降算法解释以及求解θ
ng机器学习视频笔记(二) --梯度下降算法解释以及求解θ (转载请附上本文链接--linhxx) 一.解释梯度算法梯度算法公式以及简化的代价函数图,如上图所示. 1)偏导数由上图可知,在a点 ...
监督学习：随机梯度下降算法（sgd）和批梯度下降算法（bgd）
线性回归首先要明白什么是回归.回归的目的是通过几个已知数据来预测另一个数值型数据的目标值. 假设特征和结果满足线性关系,即满足一个计算公式h(x),这个公式的自变量就是已知的数据x,函数值h(x)就 ...
[机器学习Lesson3] 梯度下降算法
1. Gradient Descent(梯度下降) 梯度下降算法是很常用的算法,可以将代价函数J最小化.它不仅被用在线性回归上,也被广泛应用于机器学习领域中的众多领域. 1.1 线性回归问题应用我们 ...
AI-2.梯度下降算法
上节定义了神经网络中几个重要的常见的函数,最后提到的损失函数的目的就是求得一组合适的w.b 先看下损失函数的曲线图,如下即目的就是求得最低点对应的一组w.b,而本节要讲的梯度下降算法就是会一步一步地 ...
Logistic回归Cost函数和J(θ)的推导（二）----梯度下降算法求解最小值
前言在上一篇随笔里,我们讲了Logistic回归cost函数的推导过程.接下来的算法求解使用如下的cost函数形式: 简单回顾一下几个变量的含义: 表1 cost函数解释 x(i) 每个样本数据点在 ...
梯度下降算法对比（批量下降/随机下降/mini-batch）
大规模机器学习: 线性回归的梯度下降算法:Batch gradient descent(每次更新使用全部的训练样本) 批量梯度下降算法(Batch gradient descent): 每计算一次梯度 ...
tensorflow随机梯度下降算法使用滑动平均模型
在采用随机梯度下降算法训练神经网络时,使用滑动平均模型可以提高最终模型在测试集数据上的表现.在Tensflow中提供了tf.train.ExponentialMovingAverage来实现滑动平均模 ...

随机推荐

spring boot 启动问题
spring boot启动报错误 Thread-2] s.c.a.AnnotationConfigApplicationContext : Closing org.springframework.co ...
npm 和bower之间的区别
(一) npm是node js的包管理器,用来下载安装node js的第三方工具包,也可以用来发布你自己开发的工具包.通过npm可以安装bower,命令如下: npm install -g bower ...
table 表格的增删和修改
如上图,图片的增删都没有问题:唯一的问题就是我改变下一行的内容时,把上面一行给覆盖了,费了好久,终于找到原因了,直接贴代码: 效果如下:
如何从零开始学习区块链技术——推荐从以太坊开发DApp开始
很多人迷惑于区块链和以太坊,不知如何学习,本文简单说了一下学习的一些方法和资源. 一. 以太坊和区块链的关系从区块链历史上来说,先诞生了比特币,当时并没有区块链这个技术和名词,然后业界从比特币中提取 ...
Jmeter-基于Ubuntu运行
这几天折腾了很久,整合了一套接口自动化的持续集成工具,先从最基础的运行Jmeter说起.由于我是用Docker部署的持续集成环境,所以接口运行必须在服务器上一:在Linux服务器先安装jdk 1:先 ...
漫谈Java IO之普通IO流与BIO服务器
今天来复习一下基础IO,也就是最普通的IO. 网络IO的基本知识与概念普通IO以及BIO服务器 NIO的使用与服务器Hello world Netty的使用与服务器Hello world 输入流与输 ...
Leetcode 27——Remove Element
Given an array and a value, remove all instances of that value in-place and return the new length. D ...
Alpha冲刺No.3
冲刺Day3 一.站立式会议终于我们遇到了我们最艰难的时候,组员也反映每天做的事情越来越少,出现了问题越来越多. 人太少,时间太少,我们没有办法一个人花足够多的时间去钻研统一个问题,或许是所以组员的 ...
C语言——第三次作业
题目1.A乘以B 1.实验代码 #include <stdio.h> int main() { int A,B,C; scanf("%d %d",&A,& ...
listview 与 button 焦点在item添加下列属性
android:descendantFocusability="blocksDescendants" http://zhaojianping.blog.51cto.com/7251 ...

Spark MLib：梯度下降算法实现

声明：本文参考《 大数据：Spark mlib(三) GradientDescent梯度下降算法之Spark实现》