bzoj1272 Gate Of Babylon

【问题描述】

【输入格式】

【输出格式】

【样例输入】

2 1 10 13

3

【样例输出】

12

【样例说明】

【数据范围】

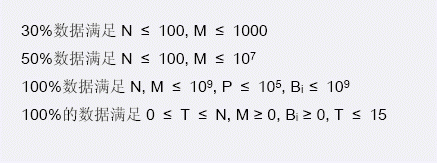
先容斥，考虑枚举哪些条件强制不满足，即直接选出b[i]+1件宝具

假设强制不满足的条件的b[i]+1的和为sum

那么剩下的就是x=m-sum个宝具

我们考虑隔板法，即C(n-1,x+n-1)=C(x,x+n-1)

但是可以小于m，即小于x

那么C(0,n-1)+C(1,n)+C(2,n+1)....+C(x,x+n-1)

根据C(i,j)=C(i-1,j-1)+C(i-1,j)

所以就变成了C(x,x+n)

然后lucas

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<cmath>
 using namespace std;
 typedef long long lol;
 lol Mod,n,t,m,b[];
 lol fac[],ifac[],inv[],ans;
 lol lucas(lol x,lol y)
 {
   if (x<||y<||x>y) return ;
   if (x==) return ;
   lol xx=x%Mod,yy=y%Mod;
   if (xx>yy) return ;
   lol s=fac[yy]*ifac[xx]%Mod*ifac[yy-xx]%Mod;
   return s*lucas(x/Mod,y/Mod)%Mod;
 }
 void dfs(lol x,lol sum,lol cnt)
 {
   if (sum>m) return;
   if (x>t)
     {
       if (cnt&)
     ans-=lucas(n,m-sum+n),ans=(ans+Mod)%Mod;
       else ans+=lucas(n,m-sum+n),ans%=Mod;
       return;
     }
   dfs(x+,sum+b[x]+,cnt+);
   dfs(x+,sum,cnt);
 }
 int main()
 {lol i;
   cin>>n>>t>>m>>Mod;
   fac[]=;inv[]=;inv[]=;ifac[]=;
   for (i=;i<Mod;i++)
     fac[i]=fac[i-]*i%Mod;
   for (i=;i<Mod;i++)
     inv[i]=(Mod-Mod/i)*inv[Mod%i]%Mod;
   ifac[]=inv[];
   for (i=;i<Mod;i++)
       ifac[i]=ifac[i-]*inv[i]%Mod;
   for (i=;i<=t;i++)
       scanf("%lld",&b[i]);
   dfs(,,);
   cout<<ans<<endl;
 }