洛谷 P1850 换教室 解题报告

P1850 换教室

题目描述

对于刚上大学的牛牛来说，他面临的第一个问题是如何根据实际情况申请合适的课程。

在可以选择的课程中，有\(2n\)节课程安排在\(n\)个时间段上。在第\(i(1≤i≤n)\)个时间段上，两节内容相同的课程同时在不同的地点进行，其中，牛牛预先被安排在教室\(c_i\)上课，而另一节课程在教室\(d_i\)进行。

在不提交任何申请的情况下，学生们需要按时间段的顺序依次完成所有的\(n\)节安排好的课程。如果学生想更换第\(i\)节课程的教室，则需要提出申请。若申请通过，学生就可以在第\(i\)个时间段去教室\(d_i\)上课，否则仍然在教室\(c_i\)上课。

由于更换教室的需求太多，申请不一定能获得通过。通过计算，牛牛发现申请更换第\(i\)节课程的教室时，申请被通过的概率是一个已知的实数\(k_i\)，并且对于不同课程的申请，被通过的概率是互相独立的。

学校规定，所有的申请只能在学期开始前一次性提交，并且每个人只能选择至多\(m\)节课程进行申请。这意味着牛牛必须一次性决定是否申请更换每节课的教室，而不能根据某些课程的申请结果来决定其他课程是否申请；牛牛可以申请自己最希望更换教室的\(m\)门课程，也可以不用完这\(m\)个申请的机会，甚至可以一门课程都不申请。

因为不同的课程可能会被安排在不同的教室进行，所以牛牛需要利用课间时间从一间教室赶到另一间教室。

牛牛所在的大学有\(v\)个教室，有\(e\)条道路。每条道路连接两间教室，并且是可以双向通行的。由于道路的长度和拥堵程度不同，通过不同的道路耗费的体力可能会有所不同。 当\(i(1≤i≤n−1)\)节课结束后，牛牛就会从这节课的教室出发，选择一条耗费体力最少的路径前往下一节课的教室。

现在牛牛想知道，申请哪几门课程可以使他因在教室间移动耗费的体力值的总和的期望值最小，请你帮他求出这个最小值。

输入输出格式

输入格式：

第一行四个整数\(n,m,v,e\)。\(n\)表示这个学期内的时间段的数量；\(m\)表示牛牛最多可以申请更换多少节课程的教室；\(v\)表示牛牛学校里教室的数量；\(e\)表示牛牛的学校里道路的数量。

第二行\(n\)个正整数，第\(i(1≤i≤n)\)个正整数表示\(c_i\) ，即第\(i\)个时间段牛牛被安排上课的教室；保证\(1≤c_i≤v\)。

第三行\(n\)个正整数，第\(i(1≤i≤n)\)个正整数表示\(d_i\)，即第\(i\)个时间段另一间上同样课程的教室；保证\(1≤d_i≤v\)。

第四行\(n\)个实数，第\(i(1≤i≤n)个实数表示\)k_i\(，即牛牛申请在第\)i$个时间段更换教室获得通过的概率。保证\(0≤k_i≤1\)。

接下来\(e\)行，每行三个正整数\(a_j, b_j, w_j\)，表示有一条双向道路连接教室\(a_j, b_j\)，通过这条道路需要耗费的体力值是\(w_j\)；保证\(1<=a_j, b_j<=v\)，\(1≤w _j≤100\)。

保证\(1≤n≤2000\)，\(0≤m≤2000\)，\(1≤v≤300\)，\(0≤e≤90000\)。

保证通过学校里的道路，从任何一间教室出发，都能到达其他所有的教室。

保证输入的实数最多包含3位小数。

输出格式：

输出一行，包含一个实数，四舍五入精确到小数点后恰好2位，表示答案。你的输出必须和标准输出完全一样才算正确。

测试数据保证四舍五入后的答案和准确答案的差的绝对值不大于\(4*10^{-3}\) 。 （如果你不知道什么是浮点误差，这段话可以理解为：对于大多数的算法，你可以正常地使用浮点数类型而不用对它进行特殊的处理）

说明

道路中可能会有多条双向道路连接相同的两间教室。 也有可能有道路两端连接的是同一间教室。

请注意区分n,m,v,e的意义, n不是教室的数量, m不是道路的数量。

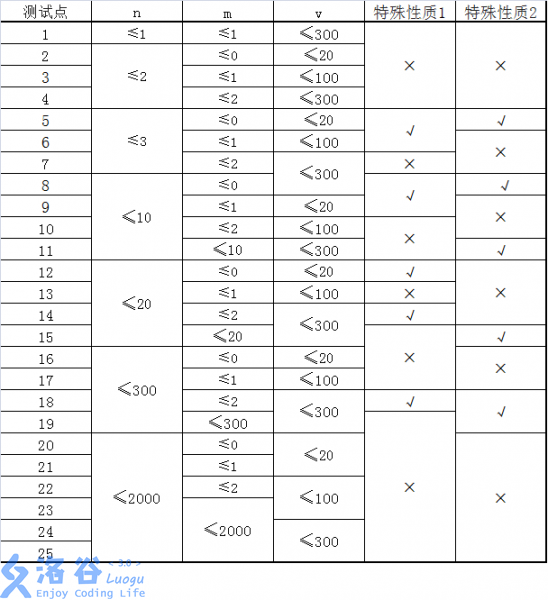
特殊性质1:图上任意两点\(a_i,b_i\),a_i≠ b_i$间,存在一条耗费体力最少的路径只包含一条道路。

特殊性质2:对于所有的\(1≤i≤n,k_i=1\)。

---

平心而论，在思想上这题确实比较裸了，但它恶心啊，经历玩天天爱跑步的？？后估计也没什么人认真的想这个题了。

首先最短路直接\(Floyd\)在\(O(n^3)\)预处理了

然后是关键的一句话要注意：这意味着牛牛必须一次性决定是否申请更换每节课的教室，而不能根据某些课程的申请结果来决定其他课程是否申请

我们是不可以根据是否更换教室来进行决策的，而很多人是注意不到这个问题的，就算注意到了，也可能不太明白两者在方程上的区别。如果根据是否更换教室居然还有88分也是很诡了。

方程：\(dp[i][j][k]\)代表\(i\)时间段已经申请了\(j\)次且第\(i\)段时间是否申请，请格外注意后四个字

转移很麻烦，但想通了也很直观

\(dp[i][j][0]=min(dp[i-1][j][0]+f[a[i-1]][a[i]],dp[i-1][j][1]+k[i-1]*f[b[i-1]][a[i]]+(1-k[i-1])*f[a[i-1]][a[i]]);\)

\(dp[i][j][1]=min(dp[i-1][j-1][0]+k[i]*f[a[i-1]][b[i]]+(1-k[i])*f[a[i-1]][a[i]],dp[i-1][j-1][1]+k[i]*k[i-1]*f[b[i-1]][b[i]]+k[i]*(1-k[i-1])*f[a[i-1]][b[i]]+(1-k[i])*k[i-1]*f[b[i-1]][a[i]]+(1-k[i])*(1-k[i-1])*f[a[i-1]][a[i]]);\)

其中，\(a[i],b[i]\)是原本/更换教室，\(k[i]\)是成功概率,\(f[i][j]\)是预处理的最短路

初始:\(f[1][0][0]=f[1][1][1]=0\)

目标:\(min_{j=0}^m(dp[n][j][0],dp[n][j][1])\)

---

Code:

#include <cstdio>
#include <cstring>
const int N=2010;
const int M=180010;
double fmin(double x,double y) {return x<y?x:y;}
int min(int x,int y) {return x<y?x:y;}
int t,c,n,m;//时间段，修改数，点，边
int a[N],b[N];//原教室，可更改教室
double k[N];//申请通过概率
int f[302][302];
void init()
{
    scanf("%d%d%d%d",&t,&c,&n,&m);
    for(int i=1;i<=t;i++)
        scanf("%d",a+i);
    for(int i=1;i<=t;i++)
        scanf("%d",b+i);
    for(int i=1;i<=t;i++)
        scanf("%lf",k+i);
    int u,v,w;
    memset(f,0x3f,sizeof(f));
    for(int i=1;i<=n;i++)
        f[i][i]=0;
    for(int i=1;i<=m;i++)
    {
        scanf("%d%d%d",&u,&v,&w);
        if(f[u][v]>w)
            f[u][v]=w,f[v][u]=w;
    }
    for(int i=1;i<=n;i++)
        f[0][i]=0;
}
void floyd()
{
    for(int l=1;l<=n;l++)
        for(int i=1;i<=n;i++)
            for(int j=1;j<=n;j++)
                f[i][j]=min(f[i][l]+f[l][j],f[i][j]);
}
double dp[N][N][2];
void DP()
{
    for(int i=1;i<=t;i++)
        for(int j=0;j<=c;j++)
            for(int l=0;l<=1;l++)
                dp[i][j][l]=1e233;
    dp[1][0][0]=dp[1][1][1]=0;
    for(int i=2;i<=t;i++)
        for(int j=0;j<=c;j++)
        {
            dp[i][j][0]=fmin(dp[i-1][j][0]+double(f[a[i-1]][a[i]])
                            ,dp[i-1][j][1]+k[i-1]*double(f[b[i-1]][a[i]])
                            +(1-k[i-1])*double(f[a[i-1]][a[i]]));
            if(j)
                dp[i][j][1]=fmin(dp[i-1][j-1][0]+k[i]*double(f[a[i-1]][b[i]])
                                +(1-k[i])*double(f[a[i-1]][a[i]])
                                ,dp[i-1][j-1][1]+k[i]*k[i-1]*double(f[b[i-1]][b[i]])
                                +k[i]*(1-k[i-1])*f[a[i-1]][b[i]]
                                +(1-k[i])*k[i-1]*f[b[i-1]][a[i]]
                                +(1-k[i])*(1-k[i-1])*f[a[i-1]][a[i]]);

        }
    double ans=1e233;
    for(int j=0;j<=c;j++)
        ans=fmin(ans,fmin(dp[t][j][0],dp[t][j][1]));
    printf("%.2lf\n",ans);
}
void work()
{
    floyd();
    DP();
}
int main()
{
    init();
    work();
    return 0;
}

---

2018.7.4