【树论 2】Kruskal 的学习和使用

Tips:本题解是【随便搞搞 1】Prim算法的学习和使用 的姊妹篇，希望先阅读Prim算法。

预习及预备知识：

克鲁斯卡尔(Kruskal)算法是实现图的最小生成树最常用的算法。

大家知道，存储图的方法有2种：邻接矩阵表示法、邻接表表示法；

这里介绍的是介于这两种之间的一种方法：边接存储法（即直接用边来存储图）

但是最小生成树是什么呢？

标准定义如下：在边子集所构成的树中，不但包括了连通图里的所有顶点，且其所有边的权值之和亦为最小。

听起来非常的带劲，我们就一起来探讨这一求最小生成树的算法！

Kruskal算法的三大特征：

●对于稠密图中求最小生成树优于Prim算法

●对于稀疏图中求最小生成树的时间复杂度O(n+m log m)

●标准Kruskal算法流程包含并查集的部分知识

算法思想：

先构造一个只含 n 个顶点、而边集为空的子图，把子图中各个顶点看成各棵树上的根结点，之后，从网的边集 E 中选取一条权值最小的边，若该条边的两个顶点分属不同的树，则将其加入子图，即把两棵树合成一棵树，反之，若该条边的两个顶点已落在同一棵树上，则不可取，而应该取下一条权值最小的边再试之。依次类推，直到森林中只有一棵树，也即子图中含有 n-1 条边为止。
时间复杂度为为O(e^2), 使用并查集优化后复杂度为 O（eloge），与网中的边数有关，适用于求边稀疏的网的最小生成树。

克鲁斯卡尔算法从另一途径求网的最小生成树。假设连通网N=（V，{E}），则令最小生成树的初始状态为只有n个顶点而无边的非连通图T=（V，{∮}），图中每个顶点自成一个连通分量。在E中选择代价最小的边，若该边依附的顶点落在T中不同的连通分量上，则将此边加入到T中，否则舍去此边而选择下一条代价最小的边。依次类推，直至T中所有顶点都在同一连通分量上为止。

图例1：

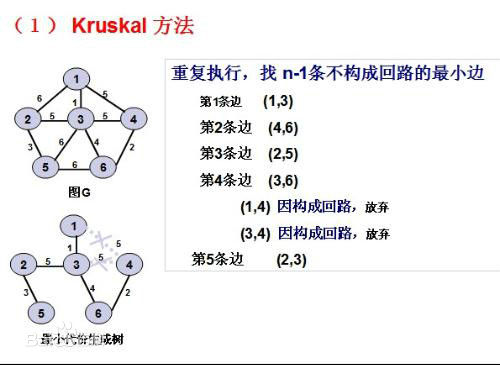
引入集合到集合的距离：对于两个集合A，B；集合A中元素和B中元素各不相同

集合A中所有元素到集合B中所有元素的距离最小值定义为集合到集合的距离

贪心方法：每一次只要连接集合到集合距离最小的两个集合，反复n-1次得出的为最小生成树

对于上例，图为依照克鲁斯卡尔算法构造一棵最小生成树的过程。代价分别为1，2，3，4的四条边由于满足上述条件，则先后被加入到T中，代价为5的两条边（1，4）和（3，4）被舍去。因为它们依附的两顶点在同一连通分量上，它们若加入T中，则会使T中产生回路，而下一条代价（=5）最小的边（2，3）联结两个连通分量，则可加入T。因此，构造成一棵最小生成树。

图例2：

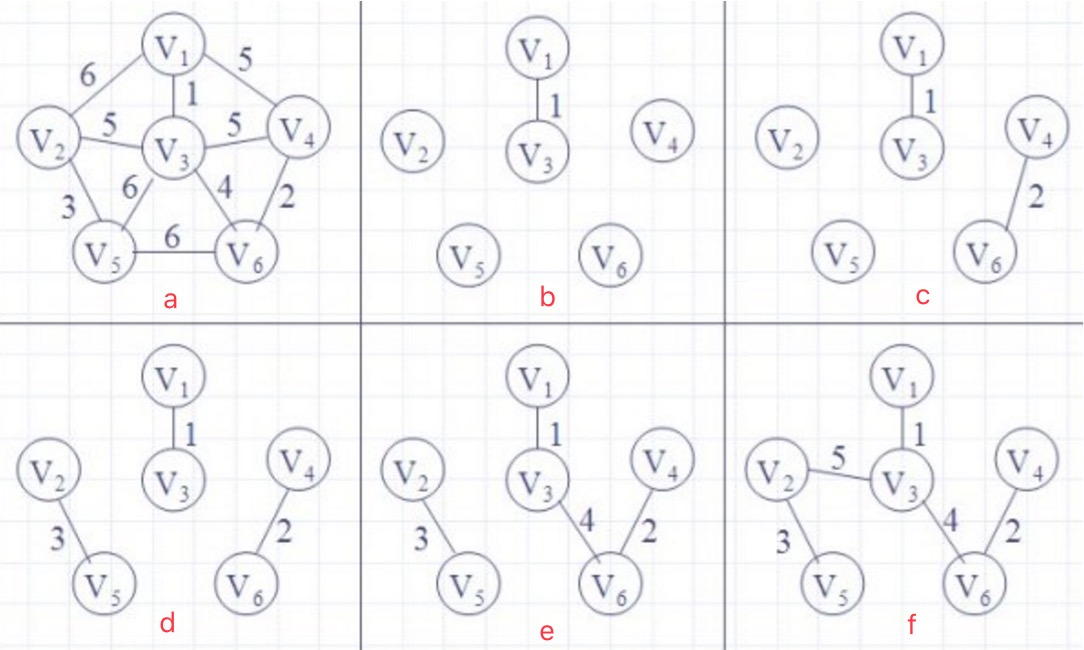
a图中是输入的一个无向图；

b中连接集合到集合距离最小的两个集合1 3，{1,3}就是一棵最小生成树;

c图连接4 6，此时图中有两个元素大于等于2个的连通分支{1,3}{4,6}分别是最小生成树;

d图连接2 3，此时图中有三个元素大于等于2个的连通分支{1,3}{4,6}{2,5}分别是最小生成树;

e图连接两个连通分支{1,3}{4,6}，图中有两个元素大于等于2个的连通分支{2,5}{1,3,4,6}分别是最小生成树;

f图连接两个连通分支{2,5}{1,3,4,6}，图中有一个元素大于等于2个的连通分支{1,2,3,4,5,6}是最小生成树;

算法完成连通分支{1,2,3,4,5,6}就是关于全图a的最小生成树;

模板分析：

---

P3366 【模板】最小生成树

题目描述

如题，给出一个无向图，求出最小生成树，如果该图不连通，则输出orz

输入输出格式

输入格式：

第一行包含两个整数N、M，表示该图共有N个结点和M条无向边。（N<=5000，M<=200000）

接下来M行每行包含三个整数Xi、Yi、Zi，表示有一条长度为Zi的无向边连接结点Xi、Yi

输出格式：

输出包含一个数，即最小生成树的各边的长度之和；如果该图不连通则输出orz

输入输出样例

输入样例#1：

4 5

1 2 2

1 3 2

1 4 3

2 3 4

3 4 3

输出样例#1：

7

说明

时空限制：1000ms,128M

数据规模：

对于20%的数据：N<=5，M<=20

对于40%的数据：N<=50，M<=2500

对于70%的数据：N<=500，M<=10000

对于100%的数据：N<=5000，M<=200000

样例解释：

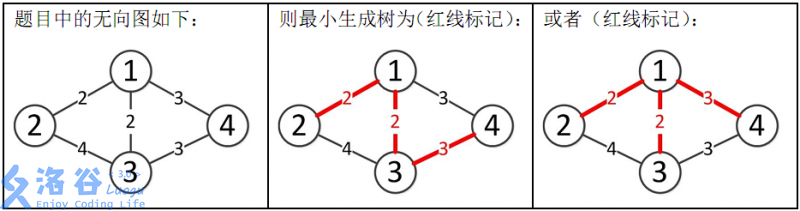
所以最小生成树的总边权为2+2+3=7

---

【分析】

对于样例，我们把1 2 3 4四点抽象为含有一个元素的子集{1}{2}{3}{4}

首先看到子集{1}{3}之间距离最小，且遍历越靠后，合并形成一个连通分支{1,3}{2}{4}

看到子集{2}{1,3}之间距离最小，合并形成一个连通分支{1,2,3}{4}
看到子集{1,2,3}{4}之间距离最小，合并形成一个连通分支{1,2,3,4}

看到连通分支{1,2,3,4}是全局的最小生成树，所以路径和为2+2+3=7

【实现】

type rec=record
 u,v,len:longint;
end;
var n,m,i:longint;
    a:array[..]of rec;
    f:array[..]of longint;
procedure qsort(l,r:longint);//按照边权从大到小排序
var i,j,mid:longint;
    t:rec;
begin
 i:=l; j:=r; mid:=a[(l+r)div ].len;
 repeat
  while a[i].len<mid do inc(i);
  while a[j].len>mid do dec(j);
  if i<=j then begin
   t:=a[i]; a[i]:=a[j]; a[j]:=t;
   inc(i); dec(j);
  end;
 until i>=j;
 if j>l then qsort(l,j);
 if i<r then qsort(i,r);
end;
function father(x:longint):longint;//求x的father，学过的都看得懂
begin
 if f[x]=x then exit(x);
 f[x]:=father(f[x]);
 exit(father(f[x]));//加了路径压缩，快一点
end;
procedure kruskal;
var tot,cnt,i,fx,fy:longint;
begin
 for i:= to m do f[i]:=i;//并查集赋初值
 qsort(,m);//快速排序
 cnt:=;
 tot:=;//初值
 for i:= to m do begin//遍历每条边
  fx:=father(a[i].u);
  fy:=father(a[i].v);//求一条边的左右两个端点的father
  if fx<>fy then begin//判断如果不是同一father则这两个点在不同的子树中
   f[fx]:=fy;//合并
   inc(cnt);//连了这条边u<--->v
   tot:=tot+a[i].len;//加上这条边的权值
  end;
  if cnt=n- then break;//加到n-1就跳
 end;
 if cnt<>n- then writeln('orz')//不符合最小生成树的边=点数-1就是不合法
 else writeln(tot);//输出各边权值和
end;
begin
 readln(n,m);
 for i:= to m do readln(a[i].u,a[i].v,a[i].len);
 kruskal;
end.

时间复杂度的推导：

初始化 所有点各自为一个森林 这一步是O(n)的
并且把边集进行从小到大排序，这一步如果使用快速排序或者堆排序是O(mlogm)

然后在这一片森林中添加边，我们知道n个点构成的树是有n-1条边，因此需要执行n-1次以下操作
从已经排序的边序列中，挑选长度最短的，且两端不在同一棵树中的一条边，判断是否是同一棵树是利用并查集进行查询，挑出这一条边之后，把两个端点代表的树合并为一棵，即并查集的合并，这也是O(1)的
注意到在选取边的过程中，只要挑选其中的n-1条，因此挑选边的n-1次挑选边的复杂度之和是O(m)的(可以理解为看最后一条连接的边在序列的第几条，最坏情况就是最后一条才能使n个点连通，因此最坏复杂度是O(m)
因此总复杂度为O(n+mlogm)

 应用:

有了这一个神奇的算法我们能干什么呢?

村庄修路，网络铺设，关于最小生成树的问题，应用比较广，学科范围广，这里给一个模板题：

Networking

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 6623		Accepted: 3608

Description

You are assigned to design network connections between certain points in a wide area. You are given a set of points in the area, and a set of possible routes for the cables that may connect pairs of points. For each possible route between two points, you are given the length of the cable that is needed to connect the points over that route. Note that there may exist many possible routes between two given points. It is assumed that the given possible routes connect (directly or indirectly) each two points in the area. 
Your task is to design the network for the area, so that there is a connection (direct or indirect) between every two points (i.e., all the points are interconnected, but not necessarily by a direct cable), and that the total length of the used cable is minimal.

Input

The input file consists of a number of data sets. Each data set defines one required network. The first line of the set contains two integers: the first defines the number P of the given points, and the second the number R of given routes between the points. The following R lines define the given routes between the points, each giving three integer numbers: the first two numbers identify the points, and the third gives the length of the route. The numbers are separated with white spaces. A data set giving only one number P=0 denotes the end of the input. The data sets are separated with an empty line. 
The maximal number of points is 50. The maximal length of a given route is 100. The number of possible routes is unlimited. The nodes are identified with integers between 1 and P (inclusive). The routes between two points i and j may be given as i j or as j i. 

Output

For each data set, print one number on a separate line that gives the total length of the cable used for the entire designed network.

Sample Input

Sample Output

参见上面的程序，prim注意有重边的处理，但是Kruskal不用担心重边的问题