poj 2369(置换群)

Permutations

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 3041		Accepted: 1641

Description

We remind that the permutation of some final set is a one-to-one mapping of the set onto itself. Less formally, that is a way to reorder elements of the set. For example, one can define a permutation of the set {1,2,3,4,5} as follows:


This record defines a permutation P as follows: P(1) = 4, P(2) = 1, P(3) = 5, etc.

What is the value of the expression P(P(1))? It’s clear, that
P(P(1)) = P(4) = 2. And P(P(3)) = P(5) = 3. One can easily see that if
P(n) is a permutation then P(P(n)) is a permutation as well. In our
example (believe us)



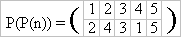
It is natural to denote this permutation by P2(n) = P(P(n)). In a
general form the defenition is as follows: P(n) = P1(n), Pk(n) =
P(Pk-1(n)). Among the permutations there is a very important one — that
moves nothing:



It is clear that for every k the following relation is satisfied:
(EN)k = EN. The following less trivial statement is correct (we won't
prove it here, you may prove it yourself incidentally): Let P(n) be some
permutation of an N elements set. Then there exists a natural number k,
that Pk = EN. The least natural k such that Pk = EN is called an order
of the permutation P.

The problem that your program should solve is formulated now in a very simple manner: "Given a permutation find its order."

Input

In
the first line of the standard input an only natural number N (1 <= N
<= 1000) is contained, that is a number of elements in the set that
is rearranged by this permutation. In the second line there are N
natural numbers of the range from 1 up to N, separated by a space, that
define a permutation — the numbers P(1), P(2),…, P(N).

Output

You
should write an only natural number to the standard output, that is an
order of the permutation. You may consider that an answer shouldn't
exceed 10⁹.

Sample Input

5
4 1 5 2 3

Sample Output

6

题意:给出一个集合 p,每次按照一个规则去换掉其中的元素,问使 p^k = p 成立的最小的 k 是多少?

题解:我们将该集合的所有置换群求出来,那么最小的k就是这些群的循环的最小公倍数,比如:

1 2 3 4 5
4 1 5 2 3
上面可以划分出两个群 (1,4,2),(3,5)这两个群的循环分别是 3 ,2 所以最小的 k 就是 3*2 = 6

#include <stdio.h>
#include <algorithm>
#include <string.h>
using namespace std;
typedef long long LL;
const int N = ;
int n;
struct Node{
    int val,id;
}node[N];
bool vis[N];
int cmp(Node a,Node b){
    return a.val < b.val;
}
int gcd(int a,int b){
    return b==?a:gcd(b,a%b);
}
int main()
{
    while(scanf("%d",&n)!=EOF){
        memset(vis,false,sizeof(vis));
        for(int i=;i<=n;i++){
            scanf("%d",&node[i].val);
            node[i].id = i;
        }
        sort(node+,node++n,cmp);
        int lcm = ;
        for(int i=;i<=n;i++){
            int loop = ;
            int t = i;
            while(!vis[t]){
                loop++;
                vis[t] = true;
                t = node[t].id;
            }
            if(loop){
                lcm = lcm/gcd(lcm,loop)*loop;
            }
        }
        printf("%d\n",lcm);
    }
    return ;
}