K：有限状态自动机

  有限状态自动机是一种特殊的状态机。它表示有限个状态以及在这些状态之间的转移和动作等行为的数学模型。有限状态自动机分为两种，一种是 确定有限状态自动机(DFA) ，一种是 非确定有限状态自动机(NFA) 。需要知道的是，对于每一种NFA都可转换为同样识别能力的DFA。

  有限状态自动机定义为五元组，即M=（S，∑，f，So，Z）。对于非确定有限状态自动机和确定有限状态自动机其五元组表示的符号的意义不完全相同，下面我们将分别对其进行说明。需要注意的是所谓的非确定，是指在某个状态输入同一个符号，状态可以迁移到不同的下一个状态，并且其可以在空符号（即没有输入符号）的时候进行状态的迁移。

确定有限状态自动机

定义:

S是一个有限状态集合。

∑是一个字母表，输入字符的集合。

f是从S x ∑*至S的子集映射函数。

S0⊆S，是 唯一 的初态。

Z⊆S，是一个终态集。

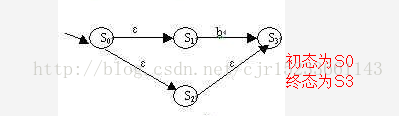
非确定有限状态自动机

定义:

S是一个有限状态集合。

∑是一个字母表，输入字符的集合。

f是从S x ∑*至S的子集映照。

S0⊆S，是一个非空 初态集。

Z⊆S，是一个终态集。

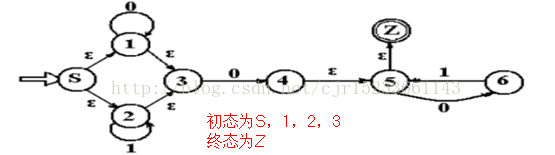
NFA与DFA

  对比于NFA与DFA，其区别仅在于初态S0，确定的有限状态自动机的S0是唯一确定的。而不确定的有限状态自动机的初态是一个集合，即有多个初态。

  由于NFA是一种状态不确定的自动机，所以这种自动机不便机器实现；DFA是有限确定状态的自动机，它的状态转换的条件都很确定，所以它比较方便机器实现，同时在识别能力也和NFA相当（相关的书中已经证明了每一种NFA都可转换为同样识别能力的DFA），所以转换为DFA是更有利于机器实现。

ps:对于正则表达式而言，每一个表达式都可以等价于一个NFA，其转化过程如图：

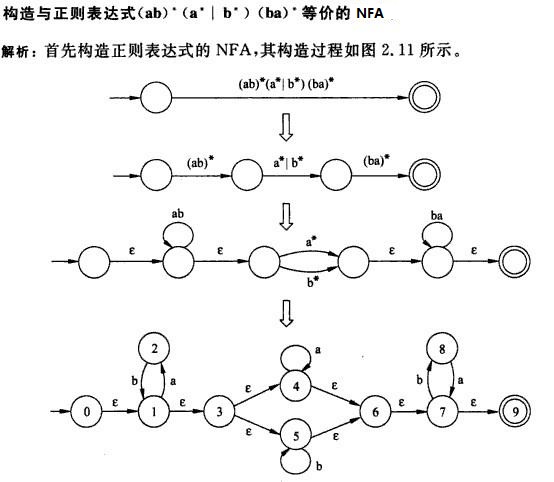
关于NFA与DFA的转化参看博文：NFA到DFA的转化

参考自: 2007年1月31日、有限状态机与有限状态自动机、有限状态自动机、非确定有限状态自动机的构建（一）——NFA的定义和实现